Cây 2-3-4

Trong khoa học máy tính, cây 2-3-4 là cây nhiều nhánh mà mỗi nút của nó có thể có đến bốn nút con và ba mục dữ liệu. Cây 2-3-4 là cây cân bằng giống như cây đỏ-đen, tuy nhiên ít hiệu quả hơn nhưng ngược lại dễ lập trình hơn.

Các số 2, 3, 4 trong cụm từ 2-3-4 có ý nghĩa là khả năng có 2-3 hoặc 4 liên kết đến các nút con có thể có được trong một nút cho trước.

Với mọi nút lá thì không có nút con, nhưng có thể chứa 1, 2 hoặc 3 mục dữ liệu, không có nút rỗng. Một cây 2-3-4 có thể có đến bốn cây con, nên được gọi là cây nhiều nhánh bậc 4.

Trong cây 2-3-4 mỗi nút có ít nhất là hai liên kết, trừ nút lá (nút không có nút con).

Tổ chức

Các khóa trong một nút

Trong một nút lá hoặc nút trong có thể có 2-3-4 khóa đại diện cho mục dữ liệu. Các khóa trong mỗi nút được sắp xếp theo thứ tự tăng dần. Tất nhiên các nút lá không có con.

Còn với các nút không phải là lá, trong từng trường hợp có số nút con như sau:

Một nút chứa một khóa luôn luôn có đúng 2 nút con. Nó được gọi là 2-nút.
Một nút chứa hai khóa luôn luôn có đúng 3 nút con. Nó được gọi là 3-nút.
Một nút chứa ba mục khóa luôn luôn có đúng 4 nút con. Nó được gọi là 4-nút.

Như vậy, một nút không phải là lá phải luôn luôn có số nút con nhiều hơn 1, so với số khóa của nó. Nói cách khác, đối với mọi nút trong có số con là l và số khóa là d, thì: l = d+ 1.

Các khóa nằm trong các nút khác nhau

Một đặc tính quan trọng của cấu trúc cây tìm kiếm nhị phân là mối liên hệ giữa các liên kết với giá trị khoá của cây con bên trái, có khoá nhỏ hơn khoá của nút đang xét và tất cả nút của cây con bên phải, có khoá lớn hơn hoặc bằng khoá của nút đang xét.

Trong cây 2-3-4 thì một cấu trúc tương tự như trên, thể hiện trong các tính chất sau:

Tất cả các nút con của cây con thứ 1 của nút cha có các khoá nhỏ hơn khoá thứ nhất của nút cha.
Tất cả các nút con của cây con thứ 2 của nút cha có các khoá lớn hơn khoá thứ nhất và nhỏ hơn khóa thứ hai của nút cha (nếu nút cha có khóa thứ hai).
Tất cả các nút con của cây con thứ 3 (nếu có) của nút cha có các khoá lớn hơn khoá thứ hai và nhỏ hơn khóa thứ ba của nút cha (nếu nút cha khóa có khóa thứ ba).
Tất cả các nút con của cây con thứ 4 (nếu có) của nút cha có các khoá lớn hơn khoá thứ ba của nút cha.

Trong cây 2-3-4, tất cả các lá đều nằm trên cùng một mức. Các nút ở mức trên thường không đầy đủ, nghĩa là chúng có thể chứa chỉ 1 hoặc 2 khóa thay vì 3 khóa.

Lưu ý rằng: cây 2-3-4 là cây cân bằng. Nó vẫn giữ được sự cân bằng ngay ca khi ta chèn các phần tử theo thứ tự tăng dần hoặc giảm dần.

Khóa tiền nhiệm và khóa kế vị

Cũng như trong cây tìm kiếm nhị phân, trong cây 2-3-4 khóa tiền nhiệm của một khóa k là khóa lớn nhất trong các khóa nhỏ hơn k, khóa kế vị là khóa nhỏ nhất trong các khóa lớn hơn k. Theo cấu trúc của cây 2-3-4, để tìm khóa tiền nhiệm và khóa kế vị của khóa k trước hết tìm nút u chứa khóa k.

Nếu u là nút trong, giả sử k là khóa thứ m của u, khi đó khóa tiền nhiệm là khóa cuối cùng của nút cực phải trong cây thứ m của nút u, còn khóa kế vị là khóa đầu tiên trong nút cực trái của cây con thứ m+1 của nút u. Nếu khóa k nằm trong nút lá u, việc tìm khóa tiền nhiệm và kế vị có khó khăn hơn, tuy nhiên, trong các ứng dụng của cây 2-3-4 không cần đến trường hợp này.

Trong hình trên đây, khóa tiền nhiệm của khóa 24 là khóa 22, còn khóa kế vị của khóa 24 là khóa 26.

Các phép biến đổi không làm thay đổi tính chất của cây 2-3-4

Dịch chuyển khóa

Phép biến đổi này chuyển một khóa từ một 3-nút hoặc 4-nút sang một nút anh em kề nó có ít hơn 3 khóa. Giả sử A là con thứ k của nút cha và A có 1 khóa là a₁ , B là nút thứ k+1 của nút cha và B có 3 khóa b₁ < b₂< b₃ . Khóa thứ k của nút cha là c_k. Khi đó ta có a₁< c_k < b₁ < b₂ <b₃ . Phép dịch chuyển sẽ chuyển khóa c_k từ nút cha xuống cuối nút A và chuyển khóa đầu tiên b₁ của nút B lên thay cho c_k. Như vậy trong phép dịch chuyển này số khóa của nút cha không thay đổ, số khóa của nút A tăng thêm một và số khóa của nút B giảm một. Để số khóa của A và B nằm trong phạm vi từ 1 đến 3, điều kiện để thực hiện phép chuyển khóa là số khóa của nút A nhỏ hơn 3 và số khóa của nút B lớn hơn 1.

Nếu nút anh em liền kề với nút u chỉ có một nút có thể tăng số khóa của u từ một nút anh em không liền kề có nhiều hơn một khóa bằng 2 hoặc 3 phép dịch chuyển liên tiếp.

Tách một nút

Phép biến đổi này tách một nút thành hai nút, nghĩa là thêm một nút anh em với nó. Như vậy số con của nút cha tăng thêm một, do đó số khóa của nút cha cũng tăng lên một. Khóa tăng thêm này được lấy từ chính nút con sẽ được tách ra. Do đó để có thể tách một nút, nút đó phải có đúng 3 khóa k1 < k2 < k3 (nó là 4-nút). Khi tách, chỉ khóa k1 được giữ lại nút ban đầu (nút này trở thành 2-nút), k3 được gán cho nút mới tạo thêm (là 3-nút), còn k2 được thêm vào nút cha. Như vậy nút ban đầu và nút mới tạo ra là anh em liền kề. Nếu nút cha đã là 4-nút thì trước khi thêm k2 vào nó cần tách chính nút cha này.

Trong trường hợp nút cần tách là nút gốc, vì nút gốc không có cha nên ngoài việc tách ra còn phải thêm một nút mới làm cha của nút ban đầu và nút mới tách ra.

Gộp hai nút

Phép gộp hai nút anh em liền kề thành một nút. Khi đó số con của nút cha giảm đi một, do đó cả số khóa của nút cha cũng giảm một. Khóa này được đưa cả vào nút mới gộp. Do đó chỉ có thể gộp hai anh em liền kề thành một nút khi cả hai là các 2-nút, nghĩa là mỗi nút chỉ có đúng một khóa, đồng thời cha của chúng phải có nhiều hơn một khóa. Sau khi gộp, nút ban đầu trở thành 4-nút, còn nút anh em được giải phóng.

Tìm một khóa trên cây 2-3-4

Để tìm một khóa k trên cây 2-3-4, trước hết ta tìm nó trong dãy khóa của nút gốc. Tại mỗi nút, nếu tìm thấy một khóa của nút bằng k thì trả về true và dừng quá trình tìm kiếm. Nếu không tìm thấy và nút đó là lá thì trả về false , còn nếu nút đó là nút trong và k nằm giữa khóa thứ m và m+1 thì tiếp tục tìm kiếm trong con thứ k của nút đó.

Chèn một khóa mới vào cây

Để chèn một khóa vào một cây 2-3-4 , trước hết tìm giá trị đó trong cây, nếu không thấy thì chèn khóa đó vào nút lá gặp tại cuối quá trình tìm kiếm. Nếu nút này có ít hơn 3 khóa thì việc thêm khóa đó vào nút đơn giản là việc sắp xếp nó cùng với các khóa đã có theo thứ tự tăng. Nếu nút là muốn chèn thêm là 4-nút thì trước khi chèn ta tách nút đó ra. Điều phức tạp xảy ra khi nút cha của nút định tách cũng là 4-nút. Khi đó trước khi tách nút này phải tách nút cha của nó.

Xóa một khóa khỏi cây 2-3-4

Nếu phép chèn một khóa vào một nút phải giải quyết trường hợp tràn với nút đầy đẫn tới thao tác tách, nghĩa là thêm một nút, thì phép xóa phải giải quyết trường hợp cạn đối với 2-nút, khi đó việc giải phóng khóa đó dẫn tới một nút rỗng, nghĩa là phải giải phóng nút này.

Phép xóa một khóa k khỏi cây 2-3-4 đòi hỏi những phân tích phức tạp hơn. Trước hết tìm nút chứa nó. Các trường hợp sau có thể xảy ra:

Trường hợp 1

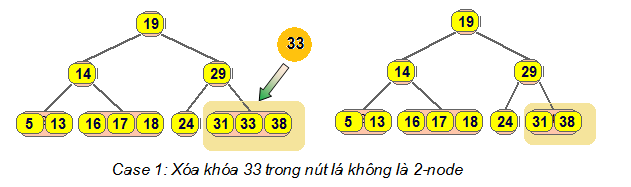
Khóa k nằm trong nút lá u và u có nhiều hơn một khóa: giải phóng khóa k khỏi u .

Trường hợp 2

Khóa k nằm trong nút lá u và u chỉ có một khóa và tồn tại nút anh em v của u có nhiều hơn một khóa thì bằng phép dịch chuyển dần có thể dịch chuyển một khóa của v đến u khiến u trở thành 3-nút và quay về trường hợp 1.

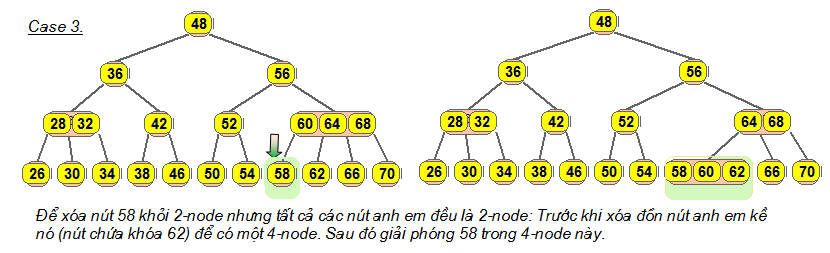
Trường hợp 3

Khóa k nằm trong nút lá u và u chỉ có một khóa và tất cả các nút anh em của u chỉ có một khóa thì bằng phép gộp u với nút anh em kề nó sẽ khiến u trở thành 3-nút và quay về trường hợp 1.

Trường hợp 4

Khóa k nằm trong nút trong u: Khi đó tìm khóa tiền nhiệm hoặc khóa kế vị của k (khóa này luôn nằm trong nút lá). Thay k bởi khóa đó, và giải phóng khóa đó tkhỏi nút chứa nó (quay về trường hợp 1). Tuy việc dùng khóa tiền nhiệm hay kế vị đều được, nhưng nên chọn khóa nào trong chúng nằm trong nút có hai khóa trở lên, nếu cả hai đều nằm trong các 2-nút thì chọn khóa nào cũng được.

Giả mã

Trong phần này ta sử dụng một số ký hiệu sau:

Nếu u là một nút thì u.keys chỉ số khóa chứa trong u, khi đó số con của nó là u.keys+1, giá trị của các khóa được chứa trong mảng u.key[1..3];
Các nút con của nút u được trỏ đến bởi mảng con trỏ u.child[1..4];
Cha của nút u được trỏ bởi biến con trỏ u.parent, nếu u là nút gốc thì u.parent = Null, nếu u là con thứ m của nút cha thì m được lưu trữ bởi biến u.order=m;
Biến u.leaf = true / false tùy theo u là lá hay nút trong.

Phép dịch chuyển

Procedure Trans_keys(u,bleft)

{chuyển một khóa từ nút v là anh (nếu bleft = true) / em (nếu bleft=false) cho u nếu v có nhiều hơn một khóa và u có ít hơn ba khóa }

1.if (u.keys>2) then return false;
2.if (bleft and then u.order=1) or (!bleft and then u.order=u.parent.keys+1) then return false;
3.m= u.order; 
4.if bleft then v:=u.parent.child(m-1) 
5.else  v:=u.parent.child(m+1);
6.  if v.keys <2 then return false;
7.	u.keys:=u.keys+1
8.	if bleft then begin { Chuyển từ nút anh kề bên trái sang }
9.	    for i:=2 to u.keys+1 do u.key(i):=u.key(i-1);
10.	    u.key(1)=u.parent.key(m);
11.	    u.parent.key(m):=v.key(v.keys);
12.	end;
13.	else begin { Chuyển từ nút em kề bên phải sang }
14.	   u.key(u.keys)=u.parent.key(m+1);
15.	   u.parent.key(m+1):=v.key(1);
16.	   for i:=1 to u.keys do v.key(i)=v.key(i+1);
17.	end;
18.	v.keys:=v.keys-1;
19.return true;

Phép tách nút

Procedure SplitNode(u);

1.if u.keys<3 then return fase;
2.if u.parent = Null then begin { tách nút gốc }
3.	   NewNode(v1);v1.key(1):=u.key(1); v1.keys:=1; v1.parent:=u;
4.	   NewNode(v2);v2.key(1):=u.key(3); v2.keys:=1; v2.parent:=u;
5.	   u.child(1).parent:=v1;u.child(2).parent:=v1; v1.child(1)=u.child(1);             v1.child(2)=u.child(2);
6.	   u.child(3).parent:=v2;u.child(4).parent:=v2; v2.child(1)=u.child(3);   v2.child(1)=u.child(1);
7.	   u.key(1)=u.key(2); u.keys:=1; end;
8.else begin { tách nút không là gốc }
9.    if u.parent.keys>2 then SplitNode(u.parent) ; { gọi đệ quy } 
10.   m:= u.order;
11.   u.parent.keys:=u.parent.keys+1;
12.   for i:=u.parent.keys-1 downto m do u.parent.key(i+1)=u.parent.key(i); 
13.   for i:=u.parent.keys downto m+1 do u.parent.child(i+1):= u.parent.child(i);
14.   u.parent.key(1)=u.key(2);
15.   NewNode(v); v.keys:=1; v.key(1):= u.key(3); v.parent=u.parent;   u.parent.child(2):=v; 
16.   v.child(1):=u.Child(3); v.child(2):=u.Child(4);
17.   u.keys:= 1;
18.end;

Gộp nút

Procedure Fusion(u) ;

1.if u.keys>1 then return false;
2.	if u.parent = Null then return false;
3.	m:=u.order;
4.	if m = 1 then v:= u.parent.child(2) else v:= u.parent.child(m-1) ;
5.	if v.keys>1 then return false ;
6.	u.keys:=3;
7.	if u.parent= Null then return false;
8.	if u.parent.keys=1 then TwoNodeAddKey(u.parent);
9.	if m:=1 then begin
10.	    u.key(2)=u.parent.key(1); u.key(3):= v.key(1);
11.	    u.child(3):=v.child(1); u.child(4):=v.child(2); v.Child(3).parent:=u; v.Child(4).parent:=u ;
12.	    for i:=1 to u.parent.keys-1 do u.key(i):= u.key(i+1);
13.	    for i:=2 to u.parent.keys  do u.parent.child(i):=u.parent.child(i+1)
14.    end;
15.	else begin 
16.	   u.key(3):= u.key(1); u.key(1):=v.key(1); u.key(2):= u.parent.key(m-1);
17.	   u.child(3):=uChild(1);u.Child(4):=u.Child(2); 
18.	   u.child(1):=v.child(1); u.child(2):=v.child(2); v.child(1).parent:=u; v.child(2).parent:=u;
19.	   for i:=m to u.parent.keys-1 do u.key(i):= u.key(i+1);
20.	   for i:=m to u.parent.keys  do u.parent.child(i):=u.parent.child(i+1);
21.	   u.parent.child(m-1):=u;
22.	end;
23.u.parent.keys:=u.parent.keys-1;
24.dispos(v);

Tăng số khóa cho 2-nút

Khi xóa một khóa trong hai nút, trước hết phải dùng phép chuyển khóa hoặc phép dồn nút để tăng số khóa của nút này. Nếu tìm được một khóa anh em có nhiều hơn một khóa có thể dùng phép dịch chuyển, nếu không có có thể dùng một phép gộp nút.

Tìm nút anh em có nhiều hơn một khóa

Procedure FindSubling(u);

1.if u.parent= Null then return 0;
2.m:=u.order;
3.k:=m+1
4.while (k≤ u.parent.keys+1) and (u.parent.child(k).keys<2) do   k:=k+1;
5.if k ≤ u.parent.keys+1 then return k; 
6.else  while (k≥1) and (u.parent.child(k).keys<2) do   k:=k-1;
7.return k;

Nếu hàm trả về 0 thì tất cả các nút anh em đều là 2-nút

Tăng số khóa cho 2-nút

Procedure TwoNodeAddKey(u);

1.If u.keys>1 then return false ;
2.if u.parent=null then fusion(u);
3.else begin  
4.    k= FindSubling(u);
5.    if k=0 then 
6.       fusion(u); 
7.    else 
8.	 if k< u.order  then 
9.	   for i:= k+1 to u.order do TransKey(u.parent.Child(i),true);        
10.	 else 
11.	   for i:= k-1 downto u.order do TransKey(u.parent.Child(i),false);
12.end;

Tìm kiếm một khóa trong cây

Tìm một khóa trong một nút

Giả sử u có n khóa. Đặt thêm các phần tử khóa hai đầu u.key(0) =  ∞ và u.key(n+1)= +∞. Khi tìm khóa k trong nút u có thể hoặc k = u.key(j) với 1 ≤ j ≤ n hoặc k thuộc một trong u.keys+1 khoảng (u.key(j),u.key(j+1)) , j=0,..,n. Trong trường hợp thứ nhất hàm trả về chỉ số khóa tìm thấy j, trong trường hợp sau hàm trả về chỉ số của cận sau trong khoảng nó tìm thấy với dấu âm. Procedure NodeSearchKey(u, k);

1.for j:=1 to u.keys do if k=u.key(j) return j;
2.j:=1;
3.while k > u.key(j) and j ≤ n do j:= j+1;
4.return j+1;

Tìm một khóa trong cây

Procedure TreeSearchKey(k; var v);

1.v:= Root.
2.k:=NodeSeachKey(v,k);
3.while k<0 and !u.leaf do begin  
4.  v:= v.child(abs(k)); 
5.  k:=NodeSeachKey(v,k); end; 
6.if k>0 return true else return false;

Tìm khóa tiền vị và khóa kế vị của một khóa

Nút chứa khóa tiền vị của khóa thứ m trong nút u

Procedure Predecessor(u,m);

1.v:= u.Child(m);
2.while !v.leaf do v:=v.child(v.keys+1);
3.return v; { khóa cuối của v là khóa cần tìm}.

Nút chứa khóa thế vị của khóa thứ m trong nút u

Procedure Successor(u,m)

1.v=u.child(m+1);
2.while !v.leaf do v:=v.child(1);
3.return v; { khóa thứ nhất của v là khóa cần tìm}.

Chèn một khóa vào cây 2-3-4

Để chèn khóa k vào cây 2-3-4 ta sử dụng thủ tục đệ quy sau với nút gốc.

Procedure NodeInsert(u,k);

1.if u= Null then begin 
2.  NewNode(v);
3.  v.Keys=1; v.key(1):= k;
4.  root:= v;
5.  v.parent := Null;
6.  end;
7.else begin 
8.  m=NodeSearchKey(u, k)
9.  if u.leaf then 
10.   if u.keys<3 then begin
11.      if m>0 then return 0
12.   else begin
13.      m=-m;  u.keys:=u.keys+1;
14.      for j:=u.keys downto m+1 do u.key(j):= u.key(j-1);
15.	  u.key(m):= k;       
16.   end; 
17.  end;
18. else begin { u có 3 khóa }
19.    m:=NodeSearchKey(u,k); 
20.    SplitNode(u);
21.    v:= u.parent.child(u.order+1);
22.      case of m
23.      1 : u.keys:=2; u.key(2):= u.key(1); u.key(1):=k; 
24.      2: u.keys:=2; u.key(2):= k; 
25.      3: v.keys:=2; v.key(2):= v.key(1); v.key(1):=k; 
26.      4: v.keys:=2; v.key(2):= k; 
27.  end;
28.else begin { u không là lá }
29.   if m>0 then return false 
30.   else NodeInsert(u.child(m),k)      
31. end;
32.end;

Xóa khóa khỏi cây 2-3-4

Xóa một khóa trong nút lá

Procedure LeafDelete(u, k);

1.if !u.leaf then return false;
2.m:=NodeSearchKey(u,k)
3.if m<0 then return false;
4.for i:= m to u.keys-1 do u.key(i):=u.key(i+1)
5.u.keys:= u.keys-1;

Xóa một khóa trong cây gốc ở đỉnh u

Procedure NodeDelete(u, k);

1.m=NodeSearch(u,k);
2.if m>0 then begin { tìm thấy k trong nút u }
3.   if u.lesft then begin  {nếu u là lá} 
4.      if (u.keys=1) and u=root then begin
5.        dispos(u); return true ; end
6.      else begin   
7.         if u.keys=1 then fusion(u);
8.         leafdelete(u,k);
9.	end;  
10.  end {nếu u là lá}
11.  else begin {tìm thấy k trong nút u là nút trong }
12.    v:= predecessor(u,m);
13.	if v.keys=1 then v:=successor(u,m) ;
14.	if v.keys=1 then fusion(u);
15.	leafdelete(v,k);     
16.	end; {tìm thấy k trong nút u là nút trong }   
17.  end { tìm thấy k trong nút u }
18. else begin { m< 0  không tìm thấy k trong nút u }
19.  m:=-m ;
20.  v:= u.child(m);
21.   if v # Null then NodeDelete(v, k)
22.   else return false ; { không có khóa k trong cây gốc u }
23. end; 
24.end; { m< 0  không tìm thấy k trong nút u }

Nguồn:

Ford, William and William Topp. Data Structures with C++ Using STL, Second Edition. Upper Saddle River, New Jersey: Prentice Hall, 2002. ISBN: 0-13-085850-1. Pages 683-290 of section 12.6: 2-3-4 Trees
More info on 2-3-4 Tree