Nhóm nhị diện cấp 6

Đồ thị Cayley với các hoán vị của một tam giác

Đồ thị chu kỳ với ma trận hoán vị của 3 phần tử (Hai phần tử sinh a và b ở đây trùng với hai phần tử a và b ở trên đồ thị Cayley.)

Bảng Cayley dưới dạng bảng cửu chương của các ma trận hoán vị

Bảng Cayley như nhóm tuyến tính tổng quát (và đặc biệt) GL (2, 2)

Trong toán học, D₃ (đôi khi được ký hiệu khác là D₆) là nhóm nhị diện bậc 3, hay nói cách khác, nhóm nhị diện cấp 6. Nó đẳng cấu với nhóm đối xứng S₃ bậc 3. Nó cũng là nhóm phi abel nhỏ nhất có thể.^[1]

Các nhóm đối xứng

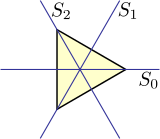
Nhóm nhị diện D₃ là nhóm đối xứng của tam giác đều, tức là tập các phép biến đổi giữ nguyên hình dạng và vị trí của tam giác này, các phép biến đổi này bao gồm quay và phản xạ và hợp của các phép này. Trong trường hợp của D₃, mọi hoán vị khả thi của các đỉnh của tam giác là một phép biến đổi. Do đó nhóm của các đối xứng này đẳng cấu với nhóm đối xứng S₃ của tất cả phép thế ba phần tử. Trường hợp này không đúng khi xét các nhóm nhị diện cấp cao hơn.

Nhóm nhị diện D₃ đẳng cấu với hai nhóm đối xứng khác trong ba chiều:

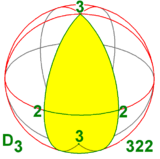
• nhóm có trục quay 3 lần và một trục quay vuông góc 2 lần: D₃
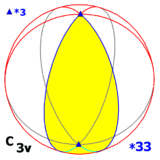
• nhóm có trục quay 3 lần trong mặt phẳng phản xạ (và do đó cũng vậy trong hai mặt phẳng phản xạ khác)): C_3v

Hoán vị của ba phần tử

Xét ba khối được tô màu đỏ, xanh và dương, theo thứ tự RGB. Nhóm đối xứng S₃ là nhóm của các hoán vị khả thi của ba khối màu này. Nếu ta ký hiệu a là hành động (hay tác động) "đổi chỗ hai khối đầu tiên",và b là hành động "đổi chỗ hai khối cuối", ta có thể viết mọi hoán vị bằng các hành động này.

Viết bằng ký hiệu phép nhân, ta thường viết xy cho hành động hợp lại "đầu tiên làm y, rồi mới x"; do đó ab là hành động RGB ↦ RBG ↦ BRG, tức là "đổi chỗ khối đầu tiên và khối cuối cùng". Nếu ta viết e là hành động "giữ nguyên vị trí của các khối" (hành động đơn vị hay hành động trung hoà), thì ta có thể viết tất cả sáu hoán vị của tập ba khối bằng cách sử dụng các hành động sau.

• e : RGB ↦ RGB hay ()
• a : RGB ↦ GRB hay (RG)
• b : RGB ↦ RBG hay (GB)
• ab : RGB ↦ BRG hay (RGB)
• ba : RGB ↦ GBR hay (RBG)
• aba : RGB ↦ BGR hay (RB)

Ký hiệu trong ngoặc tròn là ký hiệu cyclic.

Để ý rằng aa là RGB ↦ GRB ↦ RGB, giữ nguyên vị trí của các khối ; nên ta có thể viết aa = e. Tương tự như vậy,

• bb = e,
• (aba)(aba) = e, và
• (ab)(ba) = (ba)(ab) = e;

và do đó mỗi hành động trên có nghịch đảo của nó

Bằng cách xem xét, ta có thể xác định tính kết hợp và tính bao đóng (hai trong bốn tiên đề nhóm); Ví dụ chẳng hạn.

• (ab)a = a(ba) = aba, and
• (ba)b = b(ab) = bab.

Nhóm này không giao hoán bởi ab ≠ ba. Bởi nó được sinh từ các hành động cơ bản a và b, ta nói tập {a, b} sinh ra nó.

Nhóm này có biểu diễn quan hệ sau

${\displaystyle \langle r,a\mid r^{3}=1,a^{2}=1,ara=r^{-1}\rangle }$, hoặc được viết là ${\displaystyle \langle r,a\mid r^{3},a^{2},arar\rangle }$

hay

${\displaystyle \langle a,b\mid a^{2}=b^{2}=(ab)^{3}=1\rangle }$, hoặc được viết là ${\displaystyle \langle a,b\mid a^{2},b^{2},(ab)^{3}\rangle }$

trong đó a và b là các phép đổi và r = ab là phép thế cyclic. Lưu ý rằng biểu diễn quan hệ thứ hai có nghĩa là nhóm này là nhóm Coxeter (hơn nữa, mọi nhóm nhị diện và đối xứng đều là nhóm Coxeter).

Bảng nhân nhóm

Cùng với hai phần tử sinh a và b, ta định nghĩa c := aba, d := ab và f := ba, và do vậy a, b, c, d, e, và f là tất cả các phần tử của nhóm này. Ta có thể biểu diễn phép toán nhóm bằng cách dùng bảng Cayley:

*	e	a	b	c	d	f
e	e	a	b	c	d	f
a	a	e	d	f	b	c
b	b	f	e	d	c	a
c	c	d	f	e	a	b
d	d	c	a	b	f	e
f	f	b	c	a	e	d

Để ý rằng các phần tử không trung hoà và không bằng nhau chỉ giao hoán với nhau khi nó là nghịch đảo của cái còn lại. Do đó nhóm này không có tâm (tức là tâm của nhóm chỉ có phần tử trung hoà).

Tham khảo

1. Quantum field theory and beyond, 2008. For the identification of D₃ with S₃, and the observation that this group is the smallest possible non-abelian group, see p. 49.

Liên kết ngoài

• http://mathworld.wolfram.com/DihedralGroupD3.html