Kreis (Geometrie)

Dä Artikel behandlet die geometrischi Figur Kreis. Für anderi Bedütige vom Begriff «Kreis» lueg doo.

Chreis mit Mittelpunkt O, Radius R, Durchmässer D und Umfang C

Dialäkt: Oberbaselbieterdütsch

Dr Chreis isch e sehr wichtigi geometrischi Figur. Als Ortskurve in ere Eebeni isch er so definiert, das er alli Pünkt P enthaltet, wo vom Mittelpunkt M die konstant Entfärnig r (Radius) hei.

Algebrahischi Chreisdarstellige

In dr Algebra chöne verschiedenschti Formle brucht wärde, um e Kreis darzstelle. Do mol e chlini Uflischtig:

Vektorielli Gliichig

Dur d Definition vom konstante Abstand zum e Punkt M isch ganz eifach folgendi Glichig z begründe.

${\displaystyle {\overline {MP}}=r}$

Dr Abstand ${\displaystyle |{\overrightarrow {MP}}|}$ wird vektoriell dur de Betrag vom Vektor zwüsche M und P dargstellt:

${\displaystyle |{\overrightarrow {MX}}|=r}$

${\displaystyle |{\overrightarrow {0P}}-{\overrightarrow {0M}}|=r}$

Koordinategliichig

Us dr vektorielle Gliichig loht sich ganz eifach wider d Koordinate gliichig härleite. Dr Betrag vome Vektor cha me nämlig ganz eifach mitem Pythagoras bestimme ( x & y si d Koordinate vo P, u & v si d Koordinate vo M):
${\displaystyle \left|{\begin{pmatrix}x-u\\y-v\end{pmatrix}}\right|=r}$

${\displaystyle {\sqrt {(x-u)^{2}+(y-v)^{2}}}=r}$

${\displaystyle (x-u)^{2}+(y-v)^{2}=r^{2}}$

Kräisberächnig

Dr Umfang vom Kräis mit d = 1

Daarstellig von ere Nööcherig für d Kräisflechi

Chord: Kräisseene
secant: Sekante
tangent: Tangänte
radius: Radius
diameter: Durchmässer

Dr Umfang

Im Raame vo dr Elementargeometrii isch ${\displaystyle \pi }$ s Verheltnis vom Kräisumfang ${\displaystyle U}$ zum Durchmässer vom Kräis ${\displaystyle d}$, und zwar für alli Kräis. Es gältet also

${\displaystyle U=\pi \,d=2\pi \,r.}$

Mit ${\displaystyle r={\tfrac {1}{2}}d}$ isch dr Radius vom Kräis gmäint.

D Kräisflechi

Dr Flecheninhalt vo dr Kräisflechi ${\displaystyle A}$ (lat. area: Flechi) isch broportional zum Kwadrat vom Radius ${\displaystyle r}$ bzw. vom Durchmässer ${\displaystyle d}$ vom Kräis. Mä bezäichnet en au as Kräisinhalt.

${\displaystyle A=\pi r^{2}={\frac {\pi \,d^{2}}{4}}\approx 0{,}78540\;d^{2}.}$

Dr Durchmässer

Dr Durchmässer ${\displaystyle d}$ vom ene Kräis mit eme Flechiinhalt ${\displaystyle A}$ und mit em Radius ${\displaystyle r}$ loot sich dur

${\displaystyle d=2r=2{\sqrt {\frac {A}{\pi }}}\approx 1{,}1284\;{\sqrt {A}}}$

berächne.

D Chrümmig

D Chrümmig git in jedem Punkt ${\displaystyle \mathrm {P} }$ vom Kräisumfang aa, wie stark dr Kräis in dr ummiddelbare Umgääbig vom Punkt ${\displaystyle \mathrm {P} }$ von ere Graade abwiicht. D Chrümmig ${\displaystyle \kappa }$ vom Kräis im Punkt ${\displaystyle \mathrm {P} }$ loot sich dur

${\displaystyle \kappa (\mathrm {P} )={\frac {1}{r}}}$

berächne, wo ${\displaystyle r}$ wider dr Radius vom Kräis isch. Im Geegesatz zu andere mathematische Kurve het dr Kräis in jedem Punkt die gliichi Chrümmig. Usser em Kräis het nume no die Graadi e konstanti Chrümmig ${\displaystyle \kappa =0}$. Bi alle andere Kurve isch d Chrümmig vom Punkt ${\displaystyle \mathrm {P} }$ abhängig.

Witeri Formle

In de Formle unde nooche bezäichnet ${\displaystyle \alpha }$ dr Sektorwinkel im Boogemaass, ${\displaystyle \alpha '}$ dr Winkel im Graadmaass, wo d Umrächnig ${\displaystyle \alpha ={\tfrac {\pi }{180^{\circ }}}\alpha '}$ gältet. Bi dr Berächnig vo dr Flechi vom Kräisring isch ${\displaystyle r_{a}}$ dr üsseri Radius vom Kräisring und ${\displaystyle r_{i}}$ dr inneri.

Arc: Kräisbooge
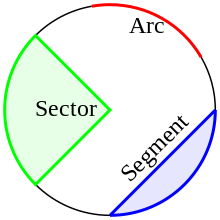
sector: Kräissektor
segment: Kräissegmänt

Formle zum Kräis
Flechi vom Kräisring	${\displaystyle A=\pi (r_{a}^{2}-r_{i}^{2})}$
Lengi vom Kräisbooge	${\displaystyle L_{B}=r\alpha }$
Flechi vom Kräissektor	${\displaystyle A_{\mathrm {SK} }={\frac {r^{2}}{2}}\alpha }$
Flechi vom Kräissegmänt	${\displaystyle A_{\mathrm {SG} }={\frac {r^{2}}{2}}\cdot \left(\alpha -\sin \alpha \right)}$
Lengi vo dr Kräisseene	${\displaystyle l_{\mathrm {KS} }=2r\sin {\frac {\alpha }{2}}}$
Hööchi vom Kräissegmänt	${\displaystyle h=r-r\cos {\frac {\alpha }{2}}}$

Litratuur

• Ilka Agricola, Thomas Friedrich: Elementargeometrie. 3. Uflaag. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-1385-5.
• Christian Bär: Elementare Differentialgeometrie. 2. Uflaag. Walter de Gruyter, Berlin 2010, ISBN 978-3-11-022458-0.
• Hartmut Wellstein, Peter Kirsche: Elementargeometrie. Eine aufgabenorientierte Einführung. Vieweg+Teubner, Wiesbade 2009, ISBN 978-3-8348-0856-1.

Weblingg

 Wikibooks: Beweis der Transzendenz von e und π — Lern- und Lehrmaterialie

• „Mathematische Basteleien“ zum Kreis
• Eric W. Weisstein: Kreis. In: MathWorld (änglisch).