جيب التمام

جيب التمام
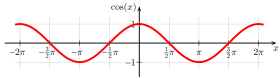
تمثيل دالة جيب التمام في جملة الإحداثيات الديكارتيّة تمثيل دالة جيب التمام في جملة الإحداثيات الديكارتيّة
تدوين	${\displaystyle \cos(x)}$ أو جتا (س) أو تجب (س)
تعريف الدالة	cos A = الضلع المجاور لزاوية في مثلث قائم/الوتر
دالة عكسية	${\displaystyle \arccos(x)}$
مشتق الدالة	${\displaystyle -\sin(x)}$
مشتق عكسي (تكامل)	${\displaystyle \sin(x)+C}$
الميزات الأساسية
زوجية أم فردية؟	زوجية
مجال الدالة	${\displaystyle \mathbb {R} =]-\infty ,+\infty [}$
المجال المقابل	${\displaystyle [-1,1]}$
دورة الدالة	2π
قيم محددة
القيمة/النهاية عند الصفر	1
الحدود الأعلى	${\displaystyle (2k\pi ,1)}$
الحدود الأدنى	${\displaystyle (\pi +2k\pi ,-1)}$
جذور الدالة	${\displaystyle {\frac {\pi }{2}}+k\pi }$
نقاط حرجة	${\displaystyle k\pi }$
نقاط ثابتة	0.7390851332152... (عدد دوتي)
ملاحظات	${\displaystyle k\in \mathbb {Z} }$
تعديل مصدري - تعديل

في الرياضيات، جَيْب التَمَام^[1] (بالإنجليزية: Cosine)‏ هو أحد الدوال المثلثية الرئيسية، وهو نسبة الضلع المجاور لزاوية إلى الوتر في مثلث ذي زاوية قائمة، حيث يكون الوتر هو الضلع المقابل للزاوية القائمة.

الدوال المثلثية هي دوال لزوايا هندسية، وهي دوال مهمة عندما يُراد دراسة مثلث أوعرض ظواهرِ دورية. يمكن تعريف هذه الدوال كنسبة لأضلاع مثلث قائم يَحتوي تلك الزاويةَ أَو بشكل أكثر عمومية كإحداثيات على دائرة مثلثية أو دائرة واحدية.

الدوال المثلثية هي دوال ترتبط بـالزاوية ، وهي مهمة في دراسة المثلثات وتمثيل الظواهر المتكررة (كالموجات). ويمكن تعريف الدوال المثلثية على أنهم نسب بين ضلعين في مثلث قائم فيه الزاوية المعنية. أو بشكل أوسع، كنسبة بين إحداثيات نقاط على دائرة الوحدة. ، ويعتبر دوما عند الإشارة إلى المثلثات أن الحديث يدور حول مثلث في سطح مستوي (مستوى إحداثي أو إقليدي)، وذلك ليكون مجموع زوايا المثلث 180 درجة دائما. وهناك ثلاثة دوال مثلثية أساسية نوضحها للزاوية A وهي:

• جيب الزاوية A، ويُرمز له بالرمز «جا A» (بالإنجليزية: Sin A)‏، ويساوي النسبة بين الضلع المقابل للزاوية مقسوما على الوتر. (a مقسومة على h)
• جيب تمام الزاوية A، ويُرمز له بالرمز «جتا A» (بالإنجليزية: Cos A)‏، ويساوي النسبة بين الضلع المجاور للزاوية مقسوما على الوتر. (b مقسومة على h)
• ظل الزاوية A ، ويُرمز له بالرمز «ظا A» (بالإنجليزية: Tan A)‏، ويساوي (tan=sin/cos)، ويساوي النسبة بين الضلع المقابل للزاوية والضلع المجاور لها. (الظل يساوي a مقسومة على b )

خصائص

دورية

دالة جيب التمام هي دالة دورية دورها 2π.

${\displaystyle \forall x\in \mathbb {R} \quad \cos(x+2\pi )=\cos x}$

هذه الخاصية تتدفق بشكل طبيعي من التعريف انطلاقا من دائرة الوحدة. بتعبير أدق، هناك رقمان حقيقيان لهما نفس جيب التمام إذا كان مجموعهم أو فرقهم ينتمي إلى ${\displaystyle 2\pi \mathbb {Z} }$.

زوجية

دالة جيب التمام هي دالة زوجية أي:

${\displaystyle \forall x\in \mathbb {R} \quad \cos(-x)=\cos x}$.

دالة عكسية

دالة جيب التمام هي دالة دورية وبالتالي غير تباينية. أيضا، نعتبر اقتصارها إلى [0,π] التي هي تقابلية عند [0,π] في المدى [-1,1] ، ثم نعرف دالتها العكسية، قوس جيب التمام:

${\displaystyle {\begin{matrix}\mathrm {arccos} :&[-1,1]&\to &[0,\pi ]\\&x&\mapsto &\arccos x\end{matrix}}}$

التي تحقق:

${\displaystyle \forall x\in [0,\pi ]\quad \arccos(\cos x)=x}$ ;

${\displaystyle \forall x\in [-1,1]\quad \cos(\arccos x)=x}$

التفاضل والتكامل (Calculus)

مشتق (أو التغير في ميل الخط المستقيم) Slope

مشتق الدالة هو مقابل جيب الزاوية.

${\displaystyle \forall x\in \mathbb {R} \quad \cos 'x=-\sin x}$.

مشتق عكسي (تكامل الدالة) Integral

طالع أيضًا: مشتق عكسي وتكامل

${\displaystyle \int \cos(x)dx=\sin(x)}$.

نهايات أو غايات (Limits)

طالع أيضًا: نهاية دالة

من أجل إلى كل عدد حقيقي x، تكون دالة أو مقترنة جيب التمام مستمرة عند النقطة a، لذلك تكون النهاية في هذه النقطة هي cos (a)، بتعبير آخر:

${\displaystyle \lim _{x\to a}\cos(x)=\cos(a)}$

أما بالنسبة لنهاية الدالة عند ±∞، فهي غير موجودة بسبب دورية الدالة

الشكل الأسي للدالة

• لدينا:

${\displaystyle {\begin{aligned}e^{i\theta }&=\cos \theta +i\sin \theta \\[5pt]e^{-i\theta }&=\cos \theta -i\sin \theta .\end{aligned}}}$

من تلك الصيغ (صيغ أويلر)، يمكن كتابة دالة جيب التمام على هذا الشكل:

${\displaystyle \cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}=\cosh(i\theta )}$

حيث i هي الوحدة التخيلية التي مربعها يساوي الواحد، بتعبير آخر: ${\displaystyle i^{2}=-1}$، و${\displaystyle \cosh \theta }$ هي دالة جيب التمام الزائدية.

قيم جيب التمام لبعض الزوايا

x (الزاوية)			جيب تمام الزاوية x
درجات	دائري	غراد	القيمة بالضبط	بالنظام العشري
0°	0	0^g	1	1
180°	${\displaystyle \pi }$	200^g	-1	-1
15°	${\displaystyle {\frac {\pi }{12}}}$	16 ^2⁄3^g	${\displaystyle {\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}}$	0,965925826289068
165°	${\displaystyle {\frac {11\pi }{12}}}$	183 1/3^g	${\displaystyle -{\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}}$	-0,965925826289068
30°	${\displaystyle {\frac {\pi }{6}}}$	33 ^1⁄3^g	${\displaystyle {\frac {\sqrt {3}}{2}}}$	0,866025403784439
150°	${\displaystyle {\frac {5\pi }{6}}}$	166 ^2⁄3^g	${\displaystyle -{\frac {\sqrt {3}}{2}}}$	-0,866025403784439
45°	${\displaystyle {\frac {\pi }{4}}}$	50^g	${\displaystyle {\frac {\sqrt {2}}{2}}}$	0,707106781186548
135°	${\displaystyle {\frac {3\pi }{4}}}$	150^g	${\displaystyle -{\frac {\sqrt {2}}{2}}}$	-0,707106781186548
60°	${\displaystyle {\frac {\pi }{3}}}$	66 ^2⁄3^g	${\displaystyle {\frac {1}{2}}}$	0,5
120°	${\displaystyle {\frac {2\pi }{3}}}$	133 ^1⁄3^g	${\displaystyle -{\frac {1}{2}}}$	-0,5
75°	${\displaystyle {\frac {5\pi }{12}}}$	83 ^1⁄3^g	${\displaystyle {\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}}$	0,258819045102521
105°	${\displaystyle {\frac {7\pi }{12}}}$	116 ^2⁄3^g	${\displaystyle -{\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}}$	-0,258819045102521
90°	${\displaystyle {\frac {\pi }{2}}}$	100^g	0	0
36°	${\displaystyle {\frac {\pi }{5}}}$	40^g	${\displaystyle {\frac {1+{\sqrt {5}}}{4}}}$	0,8090169944
54°	${\displaystyle {\frac {3\pi }{10}}}$	60^g	${\displaystyle {\frac {\sqrt {10-2{\sqrt {5}}}}{4}}}$	0,5877852523
126°	${\displaystyle {\frac {7\pi }{10}}}$	140^g

التعريف باستخدام الجداء القياسي

في هندسة المتجهات، يُعرَّف جيب التمام انطلاقا من الجداء القياسي للمتجهتين u و v ومعاييرها ||u|| و ||v|| بواسطة:

${\displaystyle \cos(u,v)={\frac {\langle u,v\rangle }{\|u\|\times \|v\|}}}$

تمثيل بياني لدالة جيب التمام

دائرة الوحدة؛ وتعرف بأن الوتر فيها يساوي 1.

هذا الشكل المتحرك يوضح حساب موجة جيبية بواسطة دائرة وحدة . الموجة الجيبية يمكن أن تمثل تيارا مترددا.

توضيح لدالة جيب التمام (بالأزرق) ${\displaystyle y=\cos {\theta }}$ كنقطة تتحرك على دائرة الوحدة بزاوية θ بالتقدير الدائري.

• في الدائرة المثلثية يعتبر جيب تمام زاوية في الدائرة المثلثية هو الإسقاط العمودي على المحور السيني (المحور الأفقي).

هذه موجة كاملة تنتشر إلى اليمين وموجة كاملة تنتشر إلى اليسار، كل منهما يعادل دورة واحدة في دائرة وحدة. ويمكن استخدامها في حسابات التيار المتردد.

وهي دالة زوجية حيث أن (Cos(-x) = Cos(x.

حساب جيب تمام الزاوية

يمكن التعبير عن جيب تمام الزاوية لزاوية x -معبرا عنها بالتقدير الدائري- بواسطة متسلسلة تايلور التالية:

${\displaystyle {\begin{aligned}\cos x&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.\end{aligned}}}$

اقرأ أيضا

• جيب الزاوية
• ظل الزاوية
• دائرة واحدية
• حساب المثلثات

مراجع

1. منير البعلبكي؛ رمزي البعلبكي (2008). المورد الحديث: قاموس إنكليزي عربي (بالعربية والإنجليزية) (ط. 1). بيروت: دار العلم للملايين. ص. 278. ISBN:978-9953-63-541-5. OCLC:405515532. OL:50197876M. QID:Q112315598.

• بوابة رياضيات