أجناس أويلر-فوكر

في نظرية الموسيقى والضبط ، أجناس أويلر-فوكر الموسيقية ، (بالإنجليزية: Euler-Fokker genus)‏ المسماة على إسم ليونهارد أويلر وأدريان فوكر ، ^[1] هي سلالم موسيقية في التنغيم العادل الذي يمكن التعبير عن نغماته كمنتجات لبعض أعضاء مجموعة متعددة من العوامل الأولية المولدة. عادة ما يتم تجاهل قوى الاثنين، بسبب الطريقة التي تسمع بها الأذن البشرية الأوكتافات على أنها متكافئة.

Euler genus {3, 5} as rectangle

Euler genus {3, 3, 5} as parallelepiped

Euler genus {3, 5, 5} as parallelepiped

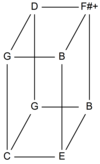
يحتوي البعد النغمي ذو الأبعاد x على عوامل x. "يمكن تمثيل مقياس أويلر-فوكر ذو البعدين في شبكة ألوان ثنائية الأبعاد و مستطيلة الشكل، و مقياس آخر بثلاثة أبعاد في شبكة ألوان ثلاثية الأبعاد على شكل كتلة، تتميز سلالم أويلر-فوكر بسرد عدد الخطوات في كل بُعد. يتم تمثيل عدد الخطوات بذكر متكرر للبعد، بحيث تنشأ أوصاف مثل [3 3 5 5]، [3 5 7]، [3 3 5 5 7 7 11 11]، إلخ." ^[2] على سبيل المثال، المجموعة المتعددة {3، 3, 7} ينتج سلم أويلر-فوكر [3، 3, 7]، والذي يحتوي على هذه النغمات:

1
  3 =3
   7=7
 3×3 =9
  3×7=21
 3×3×7=63

بعد تطبيعها لتقع ضمن الأوكتاف، تصبح هذه: 1/1 ، 9/8 ، 21/16 ، 3/2 ، 7/4 ، 63/32 . Play^ⓘ

يتم إنشاء سلالم أويلر من العوامل الأولية 3 و 5، في حين أن سلم أويلر-فوكر يمكن أن يحتوي على عوامل 7 أو أي عدد أولي أعلى. الدرجة هي عدد الفواصل التي تولد جنسا موسيقيا. بدلاً من ذلك، يمكن أيضًا تدوين [XXX...XYYY...Y]، مع x نسخة من X و y نسخة من Y، [X ^x Y ^y ]. وبالتالي فإن الدرجة هي مجموع الأسس، ويتم الحصول على عدد النغمات بإضافة واحد إلى كل أس ثم ضربها ((x+1)×(y+1)=z).

كتب أدريان فوكر الكثير من موسيقاه في سلالم أويلر-فوكر المعبر عنها في مزاج متساوي من 31 نغمة. استخدم آلان ريدوت أيضًا هذه السلالم.

وتر متعاقد كامل

يمكن أيضًا تسمية أجناس أويلر-فوكر بالوتر المتعاقد الكامل الذي صاغه أويلر، في حين صاغ فوكر المصطلح بالكامل.

يحتوي الوتر الكامل على نغمتين؛ واحدة أساسية و أخرى توجيهية، حيث تكون نغمة التوجيه مضاعفًا للنغمات الأساسية. فيما بينهما توجد نغمات أخرى يمكن اعتبارها إما مضاعفات للنغمات الأساسية أو مقسومات لنغمة الدليل ( النغمية و التناغمية). على سبيل المثال، إذا افترضنا أن 1 هو الأساس واخترنا 15 كنغمة إرشادية، نحصل على: 1:3:5:15 (السلم [35]). حاصل قسمة نغمة التوجيه على الأساسية هو "رقم التوتر" أو "الأسس" (أويلر: Exponens consonantiae ).

قام إرف ويلسون بإنشاء هياكله الخاصة التي تتداخل مع هذه المنطقة والتي تسمى "مجموعات المنتجات المركبة" أو CPS باختصار. يتم تشكيلها من خلال توليد منتجات مجموعة من العوامل التي تتضمن أيضًا 1 كعضو في المجموعة بدلاً من مجرد نقطة بداية. و هذا دفعه إلى الإشارة إلى العديد من الهياكل غير المركزية مثل الهكساني ، و الإيكوساني، و الهبدوميكونتاني.

قائمة أحناس أويلر

الدرجة الثانية
أجناس	ملحوظات
33	1/1	9/8		3/2
35	1/1		5/4	3/2		15/8
55	1/1		5/4		25/16

الدرجة الثالثة
أجناس	ملحوظات
333	1/1	9/8				3/2		27/16
335	1/1	9/8		5/4	45/32	3/2			15/8
355	1/1		75/64	5/4		3/2	25/16		15/8
555	1/1			5/4			25/16			125/64

الدرجة الرابعة
أجناس	ملحوظات
3333	1/1		9/8				81/64			3/2		27/16
3335	1/1	135/128	9/8			5/4		45/32		3/2		27/16		15/8
3355	1/1		9/8	75/64		5/4		45/32		3/2	25/16		225/128	15/8
3555	1/1			75/64		5/4			375/256	3/2	25/16			15/8	125/64
5555	1/1				625/512	5/4					25/16				125/64

مراجع

^ Rasch, Rudolph (2000). Harry Partch, p.31-2. Dunn, David, ed. (ردمك 978-90-5755-065-2).
^ Rasch, Rudolph (2000). Harry Partch, p.31-2. Dunn, David, ed. (ردمك 978-90-5755-065-2)ISBN 978-90-5755-065-2.

قراءة إضافية

[Dunn-1] Rasch, Rudolph (2000). Harry Partch, p.31-2. Dunn, David, ed. (ردمك 978-90-5755-065-2).

[مولد_تلقائيا1-2] Rasch, Rudolph (2000). Harry Partch, p.31-2. Dunn, David, ed. (ردمك 978-90-5755-065-2)ISBN 978-90-5755-065-2.

[1]

[2]