التنظيم (رياضيات)

  لمعانٍ أخرى، طالع التنظيم (توضيح).

تحدث كل من الدالتين الزرقاء والخضراء خسارة صفرية على النقاط المعطاة. لكن النموذج المتعلم يمكن أن يوجه لتفضيل الدالة الخضراء، والتي قد تعطي تعميماً أفضل على النقاط المعلومة من التوزيع غير المعلوم، من خلال ضبط مقدار لامدا (ʎ) لتحديد مقدار التنظيم.

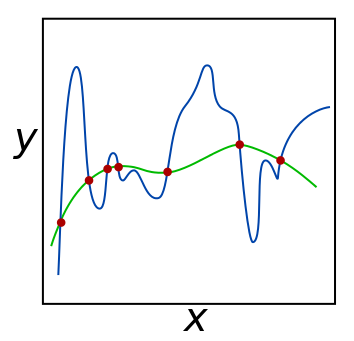
التنظيم هي عملية إضافة معلومات من أجل حل مشكلة خاطئة أو لمنع حدوث الاحكام المفرط (Overfitting) في معضلات كالتصنيف، والعملية شائعة في الرياضيات والإحصاء وعلوم الكمبيوتر ، لا سيما في التعلم الآلي.^[1]

التصنيف

أحد استخدامات التنظيم الرئيسية هي في معضلات التصنيف في التعلم الآلي، والتعلم التجريبي لأدوات التصنيف من مجموعة بيانات محدودة، والمشكلة هنا تتمثل بأن ما سينطبق على X${\displaystyle x}$ من دوال سينطبق على جميع X1, X2, X3 ..الخ. أي أن المعضلة سيتم التقليل من تحديدها وفق البيانات الموجودة.

يضاف مصطلح تنظيم (أو منظم) R يضاف إلى دالة الخسارة مضروباً بقيمة الوزن (لامدا) لمقدار التنظيم المراد اضافته:

${\displaystyle \min _{f}\sum _{i=1}^{n}V(f(x_{i}),y_{i})+\lambda R(f)}$

حيث أن V هي دالة الخسارة التي تصف كلفة التنبؤ بدالة اكس (f(x)) بوجود الناتج y، الدالة قد تكون دالة خسارة مربعة (square loss) أو دالة مفصلة للخسارة (hinge loss)؛ وكما أسلفنا، فإشارة لامدا (ʎ) تشير لمدى الوزن المراد اعطاؤه للتنظيم أو أهمية التنظيم، وتحديداً تعمل قيمة لامدا قيمة جزائية على درجة تعقيد دالة R. وقد نشأت في العلوم الأخرى فكرة مشابهة، منها ما يعرف بتنظيم تيخونوف نسبة إلى العالم أندري نيكولاييفيتش تيخونوف.

التعميم

يمكن أن يكون الدافع وراء عملية التنظيم هو اعتبارها طريقة لتحسين تعميم نموذج التعلم الآلي.

الهدف من مشكلة التعلم هنا هو العثور على دالة تناسب أو تتنبأ بالنتيجة (التصنيف) بشكل يقلل من الخطأ المتوقع على جميع المدخلات وما يقابلها من المخرجات المحتملة. الخطأ المتوقع لدالة f يُمكن صياغته كما يلي:

${\displaystyle I[f_{n}]=\int _{X\times Y}V(f_{n}(x),y)\rho (x,y)\,dx\,dy}$

لا تتوفر في مشاكل التعلم عادة، سوى مجموعة فرعية من بيانات الإدخال والمخرجات، تقاس ببعض الضوضاء. لذا، فالخطأ المتوقع غير قابل للقياس، وأفضل بديل متاح هو الخطأ التجريبي على عدد N من العينات المتاحة يكون كالآتي:

${\displaystyle I_{S}[f_{n}]={\frac {1}{n}}\sum _{i=1}^{N}V(f_{n}({\hat {x}}_{i}),{\hat {y}}_{i})}$

تقليل للتناثر

افترض أن قاموساً معيناً ذو بعد p يعبر عن دالة معينة في مجال الدالة على النحو التالي:

${\displaystyle f(x)=\sum _{j=1}^{p}\phi _{j}(x)w_{j}}$ 

تعطي مقارنة بين الكرة L1 والكرة L2 ذات البعدين حدسًا حول كيفية تحقيق التنظيم L1 للتناثر (sparsity).

فرض قيود على W يمكن أن يؤدي إلى نماذج أكثر بساطة وأكثر قابلية للفهم. هذا مفيد في العديد من التطبيقات الواقعية مثل علم الأحياء الحاسوبي. مثال على ذلك هو تطوير اختبار تنبؤي بسيط للمرض من أجل تقليل تكلفة إجراء الاختبارات الطبية مع زيادة القدرة التنبؤية إلى أقصى حد.

المحدد المعقول لقيمة التناثر هو L0، المعرف بأنه عدد العناصر غير الصفرية في W. أما تنظيم L1، فيمكن استخدامه لمقاربة القيمة المثلى لتنظيم L0 من خلال الإرخاء المحدب (convex relaxation). تجدر الإشارة إلى أن كل من L0، L1 و L2 هي أنماط من دوال التنظيم تختلف في دالة الجزاء التي تفرضها، فمثلا تفرض L1 مقداراً للجزاء يتمثل بالقيمة المجردة لمقدار التنظيم المضاف، فيما تمثل L2 دالة تربيعية لمقدار التنظيم المضاف.

المراجع

1. Bühlmann، Peter؛ Van De Geer، Sara (2011). "Statistics for High-Dimensional Data". Springer Series in Statistics: 9. DOI:10.1007/978-3-642-20192-9. ISBN:978-3-642-20191-2. If p > n, the ordinary least squares estimator is not unique and will heavily overfit the data. Thus, a form of complexity regularization will be necessary.

• بوابة تحليل رياضي
• بوابة روبوتيات
• بوابة رياضيات