بنية بلورية

نظام المكعب مركزي الجسم

مقطع من البنية البلورية لملح الطعام كلوريد الصوديوم، الذي له العدد التساندي 6.

في علم المعادن وعلم البلورات يطلق مصطلح البنية البلورية على الترتيب الفريد للذرات في البلورة.^[1][2][3] تتكون البنية البلورية من مجموعة من الذرات مرتبة بطريقة معينة في الشبكة البلورية. من الممكن تخيل وحدات البنية البلورية على أنها مجموعات من الذرات على شكل صناديق صغيرة تدعى الخلايا (وحدة خلية)، وبتكرار هذه الخلايا في الفضاء الثلاثي الأبعاد تتشكل البلورة العينية.

من أهم خصائص البلورة هو طول أضلاع الخلية، تسمى c ، b ، a والزوايا بين أضلاع الخلية وتسمى ألفا، بيتا، غاما. وتلك الستة إحداثيات تسمى إحداثيات الشبكة البلورية. تلعب البنية البلورية دوراً هاماً في تحديد خصائص البلورة مثل قابليتها على الانشقاق (الانفلاق البلوري)، التوصيل الكهربائي، نطاق الطاقة، وخصائص بصرية وخصائص مغناطيسية.

تبدأ دراسة بناء المعدن من المستوى الذري. فإذا كانت المادة معدن النحاس النقي، كان توزيع ذرات النحاس في شبكة تبلور برافيه سهلا، نظرا لتماثل جميع الذرات المكونة للبلورة. وإذا كان تركيب البلورة من مادتين مثل ملح الطعام فنحن نعرف أن ملح الطعام يتكون من كلوريد الصوديوم أي من أيونات الكلور وأيونات الصوديوم. ومن دراسة تركيب ملح الطعام عرفنا أن تركيبه يتخذ نظام المكعب. أي أنه يكوّن وحدات خلايا متساوية الأضلاع وتبلغ الزوايا بين الأضلاع 90 درجة.

البناء البلوري لملح الطعام

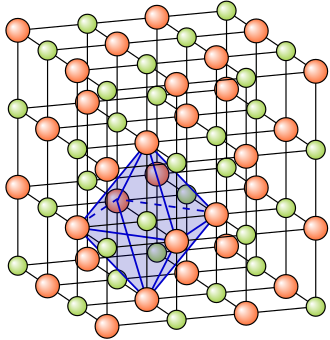
ويبين الشكل توزيع أيونات الصوديوم (أحمر)، وتوزيع أيونات الكلور (أخضر) في البلورة العيانية (الكبيرة). فنرى من اليمين إلى اليسار أيونان للكلور يتبعه أيونان للصوديوم ثم يتبعه أيونا للكلور.. وهكذا.

وإذا نظرنا إلى تتابع الأيونات من الأمام إلى الخلف وجدنا أيضا أن أيون الكلور يتبعه أيون للصوديوم ثم يتبعه أيون للكلور.. وهكذا.

وإذا نظرنا إلى توزيع الأيونات من أسفل إلى أعلى وجدنا الحال لا يختلف.

أي أن ذرات المادة (أو أيوناتها) تترتب وفق نمط منتظم متكرر، ويمكن تقسيمها إلى أصغر خلية وهي وحدة خلية وتحمل وحدة الخلية جميع الصفات الهندسية للبلورة الكبيرة.

وبفحص بلورات المعادن المختلفة وجدنا 7 أنظمة بلورية وأربع عشرة شبكة بلورية تقدم وصفاً لمواقع الذرات والاتجاهات البلورية والمستويات البلورية.

تنحصر البنية البلورية لمعظم المعادن في واحدة من ثلاثة أنواع بسيطة على الأغلب. تبدي المركبات السيراميكية ذات التركيب الكيميائي الواسع بناءات متعددة منها البسيط ومنها المعقد، ولكن معظمها (مثل السيليكات) معقدة البنية.

طرق تعيين البناء البلوري

الدراسات التي تقوم بتعيين البناء البلوري للأملاح والمعادن تعتمد على طرق القياس الآتية:

• حيود الأشعة السينية
• حيود الإلكترونات
• حيود النيوترونات

كما يمكن تعيين البناء البلوري المغناطيسي بواسطة حيود النيوترونات.

أنواع التبلور

بلورة أحادية كبيرة .

توجدالمادة الصلبة في إحدى من ثلاثة تصنيفات بالنسبة إلى بنيتها البلورية، هي:

• بلورة أحادية.
• كثيرة البلورات.
• مادة لابلورية.

وتفصيل تلك التصنيفات كالآتي:

بلورة أحادية

بلورة أحادية (بالإنجليزية:single crystal) هي مادة صلبة تتميز بامتداد الشبكة البلورية فيها من أولها إلى آخرها مكونة بلورة كبيرة منتظمة. وتتكون البلورة الأحادية مثلا عن طريق تغطيس بلورة صغيرة في محلول مشبع بمادة البلورة، وتكون البلورة الصغيرة بمثابة بذرة تتراص عليها الذرات أو الجزيئات، وتأخذ كل ذرة من ذرات المذاب موضعها بالضبط في الشبكة البلورية وبذلك تنمو البذرة إلى بلورة أحادية كبيرة.

الحبيبات البلورية

صورة لحبيبات كثيرة البلورات في الحديد الصلب .

الحبيبات البلورية هي مواد مكونة من حبيبات بلورية كثيرة لها أحجام مختلفة وعشوائية التوزيع. يمكن عن طريق ضبط عملية التبلور التوصل إلى تقليل عشوائية التوزيع بحيث تنتظم البنية البلورية ونحصل على ما يسمى بلورة أحادية.

• تبين الصورة المجاورة تكون الحديد الصلب من حبيبات، تشكل كل منها بلورة أحادية تتبع النظام البلوري الخاص بالحديد، وتتوزع فيه البلورات الأحادية توزيعا عشوائيا بالنسبة للاتجاه.

وتعتبر معظم المعادن وخزف موادا متعدد البلورات، وكثيرا ماتسمى البلورات الأحادية الصغيرة فيها بالحبيبات. ويمكن تصور كثيرة البلورات عند طحن بلورة أحادية، فكومة المسحوق تشكل مادة متعدد البلورات.

مادة لابلورية

البنية اللابلورية للسيليكا(SiO₂).

المادة اللابلورية هي مادة صلبة لا تتوزع فيها الذرات توزيع منتظما على نطاق بعيد، ويكون توزيع الذرات فيها عشوائيا، بمعنى أن توزيع الذرات فيها لا يتبع أي نظام من الأنظمة البلورية. وقد تتسم ببعض النظام على النطاق القصير (حيز 10 - 20 ذرة)، ولهاذا تسمى جوامد لابلورية. مثال على ذلك بنية الزجاج والبوليسترين وكذلك الحلوى. تتصف الجوامد ذات نظام بلوري على النطاق البعيد (أي نظام واحد يشمل البلورة من أولها إلى أخرها) بالبلورات.

أنواع الشبكات البلورية

تتكون الشبكات البلورية في الأحجار الكريمة من سبعة أنواع متشابه شكلا ولكنها مختلفة مضمونا كما جاءت في كتاب الأحجار الكريمة وتم تقسيمها علميا بحسب المحاور والزوايا ما بين تلك المحاور عند تقاطعها، وهذه النظم تحتوي على محاور ثلاثية بترتيب هندسي معين يعطي كل نظام شكله وخصائصه الفيزيائية، ويسمى العلم الذي يبحث في النظم الكرستالية باسم علم البلوريات ويطلق علية أحيانا اسم العائلة الكرستالية أو النظام الشبكي الكرستالي، والنظم الفراغية وتاتي تعريفات الخصائصية للنظام الكرستالي من التناظر المتأصل الذي يعني وتحت ظروف معينة يبقى النظام الكرستالي الشبكي على وضعه العام دون تغير. وكما هي مصورة اسفل هذه المقالة وهي كما يلي:

• النظام الثلاثي الميول: هو النظام البلوري الذي يتكون بواسطة ثلاثة محاور يتقاطعون معا بزوايا ثابتة وصحيحة اثنان من تلك المحاور لها نفس الطول على نفس المستوى والمحور الثالث الرئيسي إما أن يكون أطول أو أقصر من المحورين الآخرين. ويعتبر النظام البلوري ثلاثي الميل بلورة تحدد بواسطة ثلاثة متجهات ذات أطوال مختلفة، ولكن بشرط أن تكون غير متعامدة مع بعضها البعض. والشكل المثالي النموذجي للموشورات أربعة إما أسطح هرمية أو ثمانية أسطح هرمية متعاكسة.
• النظام الاحادي الميل: هو النظام البلوري الذي يتكون بواسطة ثلاثة متجهات. ويعتبر النظام البلوري ألاحادي الميل ذو متجهات لها أطوال مختلفة، يكون اثنان منهما متعامدان، في حين يشكل الثالث زاوية غير 90°. وبالتالي يكون للبلورات شكل منشوري.
• النظام المعيني: لديه ثلاث زوايا قائمة، لكن لديه محاور ذات أطوال مختلفة. وهي ثلاثة محاور متعامدة ومرآة تناظر ولهذا النظام أربعة أنواع منها: معيني قائم بسيط، معيني قائم مركزي القاعدة، معيني قائم مركزي الجسم، معيني قائم مركزي الوجه.
• النظام الرباعي الأضلاع: وهو النظام الذي ينشأ نتيجة جذب شبكة بلورية مكعبة باتجاه أحد المتجهات، بحيث يصبح المجال الفراغي عبارة عن منشور مستطيل له قاعدة مربعة.
• النظام المنشوري السداسي المنتظم: يعتبر النظام السداسي واحدا من النظم البلورية السبعة أو النظم الشبكية البلورية السبعة hexagonal crystal system واحد النظم العائلة البلورية الستة hexagonal crystal family وهذان النظامين لهما صلة موثقة ومتشابهين شكلا مختلفين مضمونا وبناء ولكنهما علميا ليسا نفس النظام، فالنظام السداسي العام له شبكة بلورية موحده وواحدة ولكن الاختلاف يقع في أن النظام الشبكي البلوري يحتوي على سبعة مجموعات نقطية فراغية وهذا يجعل الشبكة البلورية شبكة تحتية أما النظام العائلي البلوري فيحتوي على 12 مجموعة نقطة فراغية في مجاله ليجعل الشبكة البلورية للنظام السداسي تبدو تحتية، وكانه اتحاد بين النظام الثلاثي البلوري والنظام السداسي البلوري. ويعتبر الجرافيت خير دليل على البلورة من النظام البلوري السداسي.
• النظام السداسي: هو نظام بلوري له من ثلاث إلى أربعة محاور على مستوى واحد وبنفس الطول ويتقاطعون مع بعضهما البعض بزاوية 60 درجة وللمحور الرابع طول مختلف ويقع على زاوية صحيحة من المحاور الأخرى وله شكل كرستالي مثالي وعلى نحو نموذجي يمثل ويصور الخصائص الأساسية للموشورات والهرميات وكذلك الشكل الهرمي ذو الإثني عشر سطحا والهرم المزدوج في النظام السداسي.
• النظام التكعيبي: يدعى النظام أيسومتري أو النظام المنظوري المتساوي وله ثلاثة محاور متساوية لها نفس الطول وتتقاطع بنفس الزوايا ويعتبر النظام البلوري التكعيبي هو النظام المثالي من بين جميع الأنظمة بالإضافة إلى المكعب الثماني، المجسم المعيني، المجسم الرباعي السطوح، المجسم الإثني عشر سطحي، والعشروني أو المجسم ذو العشرون سطحا.

الشبكات البلورية السبعة

برهن عالم البلورات الفرنسي برافي أنه يوجد 14 نوع من الشبكات البلورية مهما كانت أطوال الأشعة الأولية للبلورة والزوايا المحصورة بينهم، تصنف ال14 نوعاً في 7 أصناف أو أنظمة رئيسية هي: ثلاثية الميل، أحادية الميل، معينية، رباعية، مكعبية، ثلاثية متساوية الأحرف، وسداسية.

نظام الشبكات السبعة	شبكات برافي الخاصة بكل نظام (14)
ثلاثي الميل	P
احادي الميل ذو انحدار مائل مفرد	P	C
نظام المعين القائم	P	C	I	F
النظام الرباعي الأضلاع	P	I
نظام بلوري ثلاثي متساوي الأحرف	P
نظام بلوري سداسي	P
نظام مكعبي

انظر أيضاً

• علم البلورات
• نظام بلوري
• شبكة تبلور برافيه
• مؤشرات ميلر البلورية
• شبكة ذرية
• وحدة خلية
• تبلور تجزيئي
• نظرية التراكم الكري المحدود
• منطقة بريليون
• عيب فراغي
• طابع بنائي
• بلورة أيونية

مراجع

1. Pauling، L. (1949). "A Resonating-Valence-Bond Theory of Metals and Intermetallic Compounds". وقائع الجمعية الملكية. ج. 196 ع. 1046: 343. Bibcode:1949RSPSA.196..343P. DOI:10.1098/rspa.1949.0032.
2. Liu، Gang (2015). "Dynamical equations for the period vectors in a periodic system under constant external stress". Can. J. Phys. ج. 93 ع. 9: 974. Bibcode:2015CaJPh..93..974L. DOI:10.1139/cjp-2014-0518.
3. Zhang, X. Y.؛ Suhl، H (1985). "Spin-wave-related period doublings and chaos under transverse pumping". Physical Review A. ج. 32 ع. 4: 2530–2533. Bibcode:1985PhRvA..32.2530Z. DOI:10.1103/PhysRevA.32.2530. PMID:9896377.

• بوابة الفيزياء
• بوابة الكيمياء
• بوابة علم الأحجار الكريمة والمجوهرات
• بوابة علم المواد
• بوابة علم طبقات الأرض
• بوابة كيمياء فيزيائية