زمرة دورية
ميّز عن زمرة الدائرة.| البنية الجبرية ← نظرية الزمر نظرية الزمر |
|---|
 |
|
|
في نظرية الزمر، يُقال عن زمرة أنها دوريّة[1] (بالإنجليزية: Cyclic group) إذا كان من الممكن توليدها عن طريق عنصر وحيد، فإذا كانت الزمرة تحوي عنصراً a (ويسمى مولد الزمرة) وكانت العملية المعرفة عليها هي الجداء، فإن أي عنصر من هذه الزمرة يمكن كتابته قوةً للعنصر a، أما إذا كانت العملية المعرفة هي الجمع فإن جميع العناصر يجب أن تكون من مضاعفات العنصر a.[2]
تعريف
[عدل]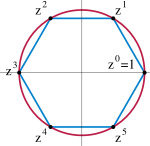خصائص
[عدل]تكون زمرة G ما دائرية إذا وجد عنصر g من G حيث كل عناصر الزمرة G تُكتب على شكل gn حيث n عدد صحيح.
أمثلة
[عدل]تمثيل الزمر الدائرية
[عدل] |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
انظر أيضا
[عدل]مراجع
[عدل]- ^ موفق دعبول؛ بشير قابيل؛ مروان البواب؛ خضر الأحمد (2018)، معجم مصطلحات الرياضيات (بالعربية والإنجليزية)، دمشق: مجمع اللغة العربية بدمشق، ص. 155، OCLC:1369254291، QID:Q108593221
- ^ p. 126: "If G has two ends, the explicit structure of G is well known: G is an extension of a finite group by either the infinite cyclic group or the infinite dihedral group." نسخة محفوظة 26 مارس 2015 على موقع واي باك مشين.
