ضرب هادامار

ضرب هادامار (بالإنجليزية: Hadamard product)‏ في الرياضيات هي عملية ثنائية تأخذ مصفوفتين من نفس البعد و تعطي مصفوفة ثالثة كل عنصر ${\displaystyle ij}$ هي جداء العناصر في ${\displaystyle ij}$ لهاتين المصفوفتين. تمت تسمية هذا الضرب على شرف عالم الرياضيات الفرنسي جاك هآدمار، أو عالم الرياضيات الألماني ایسای شور.^[1]

ضرب هادامار

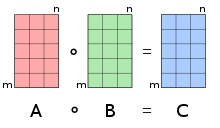
تعريف

لمصفوفتين ${\displaystyle A}$ و ${\displaystyle B}$ التي لهما أبعاد ${\displaystyle m\times n}$،^[2] ضرب هادامار ${\displaystyle A\circ B}$ أو ${\displaystyle A\odot B}$^[1][3][4][5] مصفوفة بنفس الأبعاد (أي ${\displaystyle m\times n}$ ) يتم حساب قيمها على النحو التالي:

${\displaystyle (A\circ B)_{ij}=(A\odot B)_{ij}=(A)_{ij}(B)_{ij}.}$

لم يتم تعريف هذا الضرب للمصفوفات ذات الأبعاد المختلفة.^[5]

مثال

لمصفوفتين ${\displaystyle A}$ و ${\displaystyle B}$ (${\displaystyle 3\times 3}$) ضرب هادامار يساوي:

${\displaystyle {\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}}\circ {\begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33}\end{bmatrix}}={\begin{bmatrix}a_{11}\,b_{11}&a_{12}\,b_{12}&a_{13}\,b_{13}\\a_{21}\,b_{21}&a_{22}\,b_{22}&a_{23}\,b_{23}\\a_{31}\,b_{31}&a_{32}\,b_{32}&a_{33}\,b_{33}\end{bmatrix}}.}$

خواص

• إذا ${\displaystyle A}$ و ${\displaystyle B}$ المصفوفات التي لها نفس الأبعاد لا تزيد مرتبة ضرب هادمار عن رتب الضرب لمصفوفتين:^[6]

${\displaystyle \operatorname {rank} (\mathbf {A} \circ \mathbf {B} )\leq \operatorname {rank} (\mathbf {A} )\operatorname {rank} (\mathbf {B} )}$

• إذا ${\displaystyle A}$ و ${\displaystyle B}$ و ${\displaystyle C}$ المصفوفات بنفس الأبعاد وکانت ${\displaystyle k}$ رقمًا حقيقيًا ثم:

${\displaystyle {\begin{aligned}&\mathbf {A} \circ \mathbf {B} =\mathbf {B} \circ \mathbf {A} ,\\&\mathbf {A} \circ (\mathbf {B} \circ \mathbf {C} )=(\mathbf {A} \circ \mathbf {B} )\circ \mathbf {C} ,\\&\mathbf {A} \circ (\mathbf {B} +\mathbf {C} )=\mathbf {A} \circ \mathbf {B} +\mathbf {A} \circ \mathbf {C} ,\\&\left(k\mathbf {A} \right)\circ \mathbf {B} =\mathbf {A} \circ \left(k\mathbf {B} \right)=k\left(\mathbf {A} \circ \mathbf {B} \right),\\&\mathbf {A} \circ \mathbf {0} =\mathbf {0} \circ \mathbf {A} =\mathbf {0} .\end{aligned}}}$

• للنواقل ${\displaystyle x}$ و ${\displaystyle y}$ ومصفوفاتهم القطرية ${\displaystyle D_{x}}$ و ${\displaystyle D_{y}}$ يتم إنشاء العلاقات التالية: ^[7]

${\displaystyle \mathbf {x} ^{*}(\mathbf {A} \circ \mathbf {B} )\mathbf {y} =\mathrm {tr} \left(\mathbf {D} _{\mathbf {x} }^{*}\mathbf {A} \mathbf {D} _{\mathbf {y} }\mathbf {B} ^{\mathsf {T}}\right),}$

${\displaystyle {\begin{aligned}\sum _{i}(A\circ B)_{ij}&=\left(B^{\mathsf {T}}A\right)_{jj}\\&=\left(AB^{\mathsf {T}}\right)_{ii}.\end{aligned}}}$

${\displaystyle \left(\mathbf {y} \mathbf {x} ^{*}\right)\circ \mathbf {A} =\mathbf {D} _{\mathbf {y} }\mathbf {A} \mathbf {D} _{\mathbf {x} }^{*}}$

• لقيم ذاتية من المصفوفات ${\displaystyle A}$ و ${\displaystyle B}$ العلاقة التالية تحمل: ^[8]

${\displaystyle \prod _{i=k}^{n}\lambda _{i}(\mathbf {A} \circ \mathbf {B} )\geq \prod _{i=k}^{n}\lambda _{i}(\mathbf {A} \mathbf {B} ),\quad k=1,\ldots ,n,}$

وصلات داخلية

• مصفوفة (رياضيات)
• جاك هآدمار
• ضرب المصفوفات
• قيم ذاتية ومتجهات ذاتية
• مصفوفة قطرية

مراجع

1. "Comprehensive List of Algebra Symbols". Math Vault (بالإنجليزية الأمريكية). 25 Mar 2020. Archived from the original on 2020-11-28. Retrieved 2020-09-06.
2. Million، Elizabeth (12 أبريل 2007). "The Hadamard Product" (PDF). buzzard.ups.edu. مؤرشف من الأصل (PDF) في 2020-11-28. اطلع عليه بتاريخ 2020-09-06.
3. "Hadamard product - Machine Learning Glossary". machinelearning.wtf. مؤرشف من الأصل في 2020-11-28.
4. "linear algebra - What does a dot in a circle mean?". Mathematics Stack Exchange. مؤرشف من الأصل في 2020-11-28.
5. "Element-wise (or pointwise) operations notation?". Mathematics Stack Exchange. مؤرشف من الأصل في 2020-11-28.
6. Styan، George P. H. (1973)، "Hadamard Products and Multivariate Statistical Analysis"، Linear Algebra and Its Applications، ج. 6، ص. 217–240، DOI:10.1016/0024-3795(73)90023-2، hdl:10338.dmlcz/102190
7. Horn, Roger A.; Johnson, Charles R. (2012). Matrix analysis. Cambridge University Press.
8. Hiai، Fumio؛ Lin، Minghua (فبراير 2017). "On an eigenvalue inequality involving the Hadamard product". Linear Algebra and Its Applications. ج. 515: 313–320. DOI:10.1016/j.laa.2016.11.017.

• بوابة جبر
• بوابة رياضيات