متطابقة فيثاغورس المثلثية

متطابقة فيثاغورس المثلثية، تسمى أيضًا متطابقة فيثاغورس المثلثية الأساسية^[1] أو ببساطة متطابقة فيثاغورس، هي متطابقة تعبر عن مبرهنة فيثاغورس بدلالة الدوال المثلثية. جنبا إلى جنب مع صيغ مجموع الزوايا، فهي واحدة من العلاقات الأساسية بين دالتي الجيب وجيب التمام.

المتطابقة هي:

${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1.}$

يجب الانتباه إلى هذا الترميز sin² θ يكافئ ${\textstyle (\sin \theta )^{2}}$.

البراهين وعلاقاتهم بمبرهنة فيثاغورس

تُظهِر المثلثات القائمة المتشابهة جيب وجيب تمام الزاوية θ

برهان باستخدام مثلث قائم

أي مثلثات متشابهة لها خاصية أنه إذا حددنا نفس الزاوية في كل منهم، فإن نسبة الضلعين التي تحدد الزاوية هي نفسها بغض النظر عن أي مثلث مماثل يتم تحديده، بغض النظر عن حجمه الفعلي: تعتمد النسب على الزوايا الثلاثة، وليس أطوال الأضلاع. وبالتالي بالنسبة لأي من المثلثات القائمة المتشابهة في الشكل، فإن نسبة ضلعه الأفقي إلى وتره هي نفسها، أي cos θ.

التعريفات الأولية لدالتي الجيب وجيب التمام بدلالة أضلاع المثلث القائم هي:

sin θ = المقابل/الوتر = b/c

cos θ = المجاور/الوتر = a/c

تتبع متطابقة فيثاغورس بتربيع كلا التعريفين أعلاه، وجمعهما؛ ثم يصبح الطرف الأيسر للمتطابقة:

المقابل² + المجاور²/الوتر²

والتي تساوي 1 حسب مبرهنة فيثاغورس؛ وهذا التعريف صالح لجميع الزوايا باستخدام تعريف بواسطة دائرة الوحدة.

المتطابقات المتعلقة

توضح المثلثات القائمة المتشابهة دالتي الظل والقاطع.

تطلق على كلا من المتطابقتين ${\displaystyle 1+\tan ^{2}\theta =\sec ^{2}\theta }$ و ${\displaystyle 1+\cot ^{2}\theta =\csc ^{2}\theta }$ أيضًا اسم متطابقات فيثاغورس المثلثية.^[1] إذا كان أحد ساقي المثلث القائم له طول 1، فإن ظل الزاوية المجاور لتلك الساق هو طول الساق الآخر، وقاطع الزاوية هو طول الوتر.

${\displaystyle \tan \theta ={\frac {b}{a}}}$ و ${\displaystyle \sec \theta ={\frac {c}{a}}}$

يوضح الجدول التالي المتطابقات مع علاقتهما بالمتطابقة الرئيسية:

المتطابقة الأصلية	القاسم	معادلة القاسم	المتطابقة المشتقة	المتطابقة المشتقة البديلة
${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}$	${\displaystyle \cos ^{2}\theta }$	${\displaystyle {\frac {\sin ^{2}\theta }{\cos ^{2}\theta }}+{\frac {\cos ^{2}\theta }{\cos ^{2}\theta }}={\frac {1}{\cos ^{2}\theta }}}$	${\displaystyle \tan ^{2}\theta +1=\sec ^{2}\theta }$	${\displaystyle \tan ^{2}\theta =\sec ^{2}\theta -1}$
${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}$	${\displaystyle \sin ^{2}\theta }$	${\displaystyle {\frac {\sin ^{2}\theta }{\sin ^{2}\theta }}+{\frac {\cos ^{2}\theta }{\sin ^{2}\theta }}={\frac {1}{\sin ^{2}\theta }}}$	${\displaystyle 1+\cot ^{2}\theta =\csc ^{2}\theta }$	${\displaystyle \cot ^{2}\theta =\csc ^{2}\theta -1}$

برهان باستخدام دائرة الوحدة

طالع أيضًا: دائرة الوحدة

النقطة P(x,y) على دائرة نصف قطرها 1 تصنع زاوية منفرجة θ > π/2

دالة الجيب على دائرة الوحدة (أعلى) وتمثيلها البياني (أسفل)

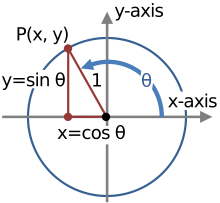
تعرف دائرة الوحدة المتمركزة في الأصل في المستوى الإقليدي بالمعادلة التالية:^[2]

${\displaystyle x^{2}+y^{2}=1.}$

إذا أعطيت الزاوية θ، هناك نقطة فريدة P على دائرة الوحدة تصنع زاوية θ انطلاقًا من المحور x، والإحداثيات x و y ل P:^[3]

${\displaystyle x=\cos \theta }$ و ${\displaystyle y=\sin \theta }$

وبالتالي، من معادلة دائرة الوحدة:

${\displaystyle \cos ^{2}\theta +\sin ^{2}\theta =1}$

متطابقة فيثاغورس.

برهان باستخدام متسلسلة القوى

يمكن أيضًا تعريف الدوال المثلثية باستخدام متسلسلة القوى، وهي (لزاوية تقاس بالراديان):^[4][5]

${\displaystyle {\begin{aligned}\sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1},\\\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}.\end{aligned}}}$

باستخدام قانون الضرب الشكلي لمتسلسلة القوى في ضرب وقسمة متسلسلة القوى (تم تعديله بشكل مناسب ليراعي شكل المتسلسلة هنا)، نحصل على:

${\displaystyle {\begin{aligned}\sin ^{2}x&=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{\frac {(-1)^{i}}{(2i+1)!}}{\frac {(-1)^{j}}{(2j+1)!}}x^{(2i+1)+(2j+1)}\\&=\sum _{n=1}^{\infty }\left(\sum _{i=0}^{n-1}{\frac {(-1)^{n-1}}{(2i+1)!(2(n-i-1)+1)!}}\right)x^{2n}\\&=\sum _{n=1}^{\infty }\left(\sum _{i=0}^{n-1}{2n \choose 2i+1}\right){\frac {(-1)^{n-1}}{(2n)!}}x^{2n},\\\cos ^{2}x&=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{\frac {(-1)^{i}}{(2i)!}}{\frac {(-1)^{j}}{(2j)!}}x^{(2i)+(2j)}\\&=\sum _{n=0}^{\infty }\left(\sum _{i=0}^{n}{\frac {(-1)^{n}}{(2i)!(2(n-i))!}}\right)x^{2n}\\&=\sum _{n=0}^{\infty }\left(\sum _{i=0}^{n}{2n \choose 2i}\right){\frac {(-1)^{n}}{(2n)!}}x^{2n}.\end{aligned}}}$

لاحظ أنه في التعبير عن sin²، يجب أن يكون n على الأقل 1، بينما في التعبير عن sin²، فإن الحد الثابت يساوي 1. والحدود المتبقية من مجموعها (مع إزالة العوامل المشتركة):

${\displaystyle \sum _{i=0}^{n}{2n \choose 2i}-\sum _{i=0}^{n-1}{2n \choose 2i+1}=\sum _{j=0}^{2n}(-1)^{j}{2n \choose j}=(1-1)^{2n}=0}$

حسب مبرهنة ذو الحدين:

${\displaystyle \sin ^{2}x+\cos ^{2}x=1\ ,}$

وهو المطلوب اثباته.

برهان باستخدام المعادلة التفاضلية

يمكن تعريف الجيب وجيب التمام كحللين للمعادلة التفاضلية:^[6]

${\displaystyle y''+y=0}$

تحققان على التوالي y(0) = 0, y′(0) = 1 و y(0) = 1, y′(0) = 0. يستنتج من نظرية المعادلات التفاضلية العادية أن الحل الأول هي دالة الجيب، والحل الثاني، جيب التمام، هي مشتقة الحل الأول، ويترتب على ذلك أن مشتق جيب التمام هو مقابل الجيب. المتطابقة تعادل التأكيد على أن الدالة:

${\displaystyle z=\sin ^{2}x+\cos ^{2}x}$

ثابتة وتساوي 1. تعطي الاشتقاق باستخدام قاعدة السلسلة:

${\displaystyle {\frac {d}{dx}}z=2\sin x\ \cos x+2\cos x\ (-\sin x)=0\ ,}$

إذن، z ثابتة حسب مبرهنة القيمة الوسطى. تؤكد الحساب أن z(0) = 1، و z ثابتة إذن z = 1 لكل x.

المراجع

1. Lawrence S. Leff (2005). PreCalculus the Easy Way (بالإنجليزية) (7th ed.). Barron's Educational Series. p. 296. ISBN:0-7641-2892-2. Archived from the original on 2020-06-17.
2. يمكن إيجاد هذه المعادلة باستخدام صيغة المسافة ${\displaystyle d={\sqrt {x^{2}+y^{2}}}}$ بالنسبة للمسافة من الأصل إلى النقطة ${\displaystyle (x,\ y)}$. طالع: Cynthia Y. Young (2009). Algebra and Trigonometry (بالإنجليزية) (2nd ed.). Wiley. p. 210. ISBN:0-470-22273-5. Archived from the original on 2024-10-09. This approach assumes Pythagoras' theorem. Alternatively, one could simply substitute values and determine that the graph is a circle.
3. توماس دبليو. هانغرفورد, Douglas J. Shaw (2008). "§6.2 The sine, cosine and tangent functions". Contemporary Precalculus: A Graphing Approach (ط. 5th). Cengage Learning. ص. 442. ISBN:0-495-10833-2. مؤرشف من الأصل في 2016-08-27.
4. James Douglas Hamilton (1994). "Power series". Time series analysis (بالإنجليزية). Princeton University Press. p. 714. ISBN:0-691-04289-6. Archived from the original on 2016-09-21.
5. Steven George Krantz (2005). "Definition 10.3". Real analysis and foundations (بالإنجليزية) (2nd ed.). CRC Press. pp. 269–270. ISBN:1-58488-483-5. Archived from the original on 2016-09-26.
6. Tyn Myint U., Lokenath Debnath (2007). "Example 8.12.1". Linear partial differential equations for scientists and engineers (ط. 4th). Springer. ص. 316. ISBN:0-8176-4393-1. مؤرشف من الأصل في 2016-04-07.

• بوابة رياضيات