مثلث متساوي الأضلاع

مثلث متساوي الأضلاع

معلومات عامة

النوع	القائمة ... regular convex polygon ^(en) — مثلث متساوي الساقين — مبسط — مضلع قابل للإنشاء — مضلع متساوي الأضلاع — مضلع متساوي الزوايا — acute triangle ^(en)
رمز شليفلي	{3}

تعديل - تعديل مصدري - تعديل ويكي بيانات

مثلث متساوي الأضلاع.

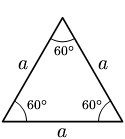
في الهندسة الرياضية، المثلث المتساوي الأضلاع (بالإنجليزية: Equilateral triangle)‏ هو مثلث جميع أضلاعه متساوية الطول.^[1][2][3] وفي الهندسة الإقليدية تكون جميع زوايا المثلث المتساوي الأضلاع متساوية القياس وقياس كل منهما °60.

المثلث المتساوي الأضلاع هو مضلع منتظم له ثلاثة أضلاع وبالتالي من الممكن تسميته مثلث منتظم.

خصائص أساسية

• كل المثلثات المتساوية الأضلاع متشابهة.
• الارتفاع في المثلث المتساوي الأضلاع ينصف الضلع المتعلق به.
• المتوسط في المثلث المتساوي الأضلاع عمودي على الضلع الذي ينصفه.
• يحقق المثلث المتساوي الأضلاع مبرهنة فيفياني.
• AD قطعة مستقيمة في المثلث المتساوي الأضلاع AD :ABC ارتفاع ${\displaystyle \Leftrightarrow }$ AD متوسط ${\displaystyle \Leftrightarrow }$ AD منصف للزاوية A.
• P نقطة في المثلث المتساوي الأضلاع P :ABC مركز قائم ${\displaystyle \Leftrightarrow }$ P نقطة وسطى ${\displaystyle \Leftrightarrow }$ P مركز الدائرة الداخلية المماسة للمثلث ABC.

طول الارتفاع

إذا كان a طول ضلع المثلث المتساوي الأضلاع، فإن طول الارتفاع فيه يعطى بالقانون:

${\displaystyle h={\frac {a{\sqrt {3}}}{2}}}$

البرهان:

إذا كان ABC مثلثاً متساوي الأضلاع طول ضلعه a و AH ارتفاع فيه قدمه H فإن:

H منتصف BC ( من خواص المثلث المتساوي الأضلاع ABC ).

بتطبيق مبرهنة فيثاغورس على AHC

${\displaystyle a^{2}=AH^{2}+({\frac {a}{2}})^{2}}$

${\displaystyle \Rightarrow AH^{2}={\frac {3{a}^{2}}{4}}}$

${\displaystyle \Rightarrow AH={\frac {a{\sqrt {3}}}{2}}}$

وهو المطلوب إثباته.

المساحة

إذا كان a طول ضلع المثلث المتساوي الأضلاع، فإن مساحته تعطى بالقانون:

${\displaystyle Area={\frac {a^{2}{\sqrt {3}}}{4}}}$

البرهان:

مساحة المثلث = ½ الارتفاع × القاعدة

مساحة المثلث = ½ ${\displaystyle {\frac {a{\sqrt {3}}}{2}}}$ × ${\displaystyle a\,}$

${\displaystyle \Leftarrow }$ مساحة المثلث المتساوي الأضلاع = ${\displaystyle {\frac {a^{2}{\sqrt {3}}}{4}}}$

مبرهنات مهمة

• تنص مبرهنة مورلي على أنه في أي مثلث، النقط الثلاث حيث يلتقي مثلِّثات الزوايا المتحادية تُكون مثلثا متساوي الأضلاع.
• مبرهنة نابليون
• مبرهنة فيفياني
• مبرهنة بومبي
• تنص صيغة لمتباينة المحيط الثابت تخص المثلثات، أن المثلث ذا المساحة القصوى عندما يكون المحيط ثابتا هو المثلث المتساوي الأضلاع.

خصائص أخرى

مثلث متساوي الأضلاع، أطوال أضلاعه متساوية (a=b=c)، وقياسات زواياه متساوية (${\displaystyle \alpha =\beta =\gamma =60^{\circ }}$) وارتفاعاته متساوية (h_a=h_b=h_c).

بفرض طول الضلع a، والارتفاع h، فإن:

• طول نصف قطر الدائرة المحيطة هو: ${\displaystyle R={\frac {a}{\sqrt {3}}}={\frac {2h}{3}}}$
• طول نصف قطر الدائرة الداخلية هو: ${\displaystyle r={\frac {a}{2{\sqrt {3}}}}={\frac {R}{2}}={\frac {h}{3}}}$
• حسب مبرهنة أويلر، فإن الدائرة المحيطة والدائرة المحاطة بمثلث متساوي الساقين لهما مركز واحد.
• المثلث ذو المساحة القصوى المحاط بدائرة محددة هو مثلث متساوي الأضلاع، والمثلث ذو المساحة الصغرى المحيط بدائرة معلومة هو مثلث متساوي الأضلاع.
• نسبة مساحة الدائرة المحاطة بمثلث متساوي الأضلاع إلى مساحته هي: ${\displaystyle {\frac {\pi }{3{\sqrt {3}}}}}$، وهذه النسبة أكبر ما تكون لمثلث متساوي الأضلاع من غيره.
• نسبة مساحة مثلث متساوي الأضلاع إلى مربع محيطه هي ${\displaystyle {\frac {1}{12{\sqrt {3}}}}}$، وهذه النسبة أكبر ما تكون لمثلث متساوي الأضلاع من غيره.

الإنشاء الهندسي

مثلث متساوي الأضلاع ينشئ بسهولة بواسطة الفرجار والمسطرة.

انظر أيضاً

• مثلث
• مبرهنة فيفياني
• مبرهنة فيثاغورس
• مثلثات قائمة خاصة
• قوانين مساحة المثلث

مراجع

1. De، Prithwijit (2008). "Curious properties of the circumcircle and incircle of an equilateral triangle". Mathematical Spectrum. ج. 41 ع. 1: 32–35.
2. Community - Art of Problem Solving نسخة محفوظة 13 أكتوبر 2016 على موقع واي باك مشين.
3. Minda، D.؛ Phelps، S. (2008). "Triangles, ellipses, and cubic polynomials". American Mathematical Monthly. ج. 115 ع. October: 679–689. JSTOR:27642581.

وصلات خارجية

إيريك ويستاين، إنشاء المثلث المتساوي الأضلاع، ماثوورلد Mathworld (باللغة الإنكليزية).

• بوابة رياضيات
• بوابة هندسة رياضية