نظرية البحث الأمثل عن الطعام

رحيق النحل العامل ليس فقط لأنفسهم، ولكن لمجتمعهم كله. تتنبأ نظرية البحث الأمثل عن الطعام أن هذه النحلة سوف تتغذى بطريقة تزيد من صافي إنتاج الخلية من الطاقة.

نظرية البحث الأمثل عن الطعام (بالإنجليزية: Optimal foraging theory)‏ هي نموذج من علم البيئة السلوكي يساعد على التنبؤ بكيفية تصرف الحيوان عند البحث عن الطعام.

على الرغم من أن الحصول على الطعام يمدّ الحيوان بالطاقة، إلا أن البحث عن الطعام والتقاطه يتطلب طاقة ووقت. ولتحقيق أقصى قدر من اللياقة، يتبنى الحيوان استراتيجية بحث عن الطعام ^{[الإنجليزية]} توفر أكبر فائدة (طاقة) بأقل تكلفة، ممّا يزيد من صافي الطاقة المكتسبة. وتساعد النظرية في التنبؤ بأفضل استراتيجية يمكن للحيوان استخدامها لتحقيق هذا الهدف.

نظرية البحث الأمثل عن الطعام هي تطبيق بيئي للنموذج الأمثل ^{[الإنجليزية]}. تفترض هذه النظرية أن نمط البحث عن الطعام الأكثر فائدة اقتصاديًا في الأنواع سُيختار من خلال الانتقاء الطبيعي.^[1] وعند استخدام نظرية البحث الأمثل عن الطعام لنمذجة سلوك البحث عن الطعام، يُقال إن الكائنات الحية تعظم متغيرًا يُعرف بالعملة، مثل معظم الطعام لكل وحدة زمنية. بالإضافة إلى ذلك، فإن قيود البيئة هي متغيرات أخرى يجب أخذها في الاعتبار. وتُعرف القيود على أنها عوامل يمكن أن تحدّ من قدرة البحث عن الطعام على تعظيم العملة. وتُعرَّف قاعدة القرار الأمثل، أو أفضل استراتيجية للبحث عن الطعام للكائن الحي، على أنها القرار الذي يزيد العملة إلى أقصى حد في ظل قيود البيئة، وتحديد قاعدة القرار الأمثل هو الهدف الأساسي لهذه النظرية.^[2]

بناء نموذج أمثل للبحث عن الطعام

يولّد النموذج الأمثل للبحث عن الطعام توقعات كمية تتعلق بكيفية كائنات الحياة تعظم لياقتها أثناء البحث عن الطعام، ويتضمن عملية بناء النموذج تحديد العملة المستخدمة، والقيود الموجودة، وقاعدة القرار المناسبة للباحث عن الطعام.^[2]

تُعرف "العملة" في هذا السياق على أنها الوحدة التي يحاول الحيوان تحسينها وتحقيق أقصى استفادة منها. كما أنها فرضية للتكاليف والفوائد التي تتحملها هذه الحيوانات.^[3] على سبيل المثال، يحصل بعض الباحثين عن الطعام على الطاقة من الطعام ولكنهم يتحملون تكلفة البحث عن هذا الطعام: الوقت والطاقة التي يستهلكونها في البحث يمكن أن تستخدم بدلاً من ذلك في أنشطة أخرى مثل البحث عن شريك حياة أو حماية الصغار. لذلك، يكون في مصلحة الحيوان تحقيق الفوائد بأقل تكلفة ممكنة. وبالتالي، يمكن تحديد العملة في هذه الحالة على أنها الصافي من الطاقة المكتسبة في الوحدة الزمنية.^[2] ومع ذلك، قد يكون الوقت الذي يستغرقه الحيوان الباحث عن الطعام في الهضم بعد تناول الطعام تكلفة أكثر أهمية بالنسبة لحيوان آخر بدلاً من الوقت والطاقة التي يستهلكها في البحث عن الطعام. في هذه الحالة، يمكن تحديد العملة على أنها الصافي من الطاقة المكتسبة في الوحدة الزمنية للهضم بدلاً من الوحدة الزمنية العادية.^[4] وعلاوة على ذلك، يمكن أن تتوقف الفوائد والتكاليف على المجتمع الذي يعيش فيه الكائن الباحث عن الطعام. على سبيل المثال، يميل الكائن الباحث عن الطعام الذي يعيش في خلية نحل إلى البحث بطريقة تحقق أقصى كفاءة لمجتمع النحل بدلاً منها نفسه.^[3] ومن خلال تحديد العملة، يمكن تصميم فرضية حول الفوائد والتكاليف الأهمية للمبحث المعني.

أما القيود فهي فرضيات حول القيود المفروضة على الحيوان، فقد تكون هناك قيود على كفاءة البحث عن الطعام نتيجة لسمات البيئة أو فيزيولوجية الحيوان، ويمكن أن تؤثر هذه القيود على كفاءتهم في البحث. على سبيل المثال، يمكن أن يكون الوقت الذي يستغرقه المبحث للوصول من موقع التعشيش إلى موقع البحث عن الطعام عائقًا. كما يمكن أن يكون الحد الأقصى لعدد العناصر الغذائية التي يمكن للكائن الباحث عن الطعام حملها إلى موقع التعشيش عائقًا آخر. ويمكن أيضًا أن تواجه الحيوانات قيودًا اعتقادية، مثل الحدود التي تفرضها القدرات التعلمية والذاكرة.^[2] كلما زادت القيود التي يمكن تحديدها في نظام معين، زادت القوة التنبؤية للنموذج.^[5]

الشكل رقم 1. الطاقة المكتسبة من كل تكلفة (E) في اعتماد استراتيجية البحث عن الطعام x. مستمد من باركر وسميث.^[6]

بالنظر إلى الفرضيات المتعلقة بالعملة والقيود، فإن قاعدة القرار الأمثل هي توقع النموذج لما يجب أن تكون عليه استراتيجية البحث الأفضل للحيوان.^[2] يمكن أن تشمل أمثلة لقواعد القرار الأمثل عدد العناصر الغذائية الأمثل التي يجب على الحيوان حملها إلى موقع التعشيش، أو الحجم الأمثل للعنصر الغذائي الذي يجب على الحيوان تناوله. يوضح الشكل رقم 1 مثالا على كيفية تحديد قاعدة القرار الأمثل من خلال نموذج رسومي.^[6] يمثل منحنى كسب الطاقة لكل تكلفة (E) لاعتماد استراتيجية البحث عن الطعام x. كسب الطاقة حسب التكلفة هو العملة التي تُحسن. تحدد قيود النظام شكل هذا المنحنى. قاعدة القرار الأمثل (x*) هي الإستراتيجية التي تكون فيها العملة، مكاسب الطاقة لكل تكلفة، هي الأكبر. يمكن أن تبدو نماذج البحث الأمثل عن الطعام مختلفة جدًا وتصبح معقدة للغاية، اعتمادًا على طبيعة العملة وعدد القيود التي توضع في الاعتبار. ومع ذلك، تظل المبادئ العامة للعملة والقيود وقاعدة القرار الأمثل كما هي لجميع النماذج.

لاختبار النموذج، يمكن مقارنة الاستراتيجية المتوقعة بسلوك الحيوان الفعلي في البحث عن الطعام. إذا كان النموذج يتطابق بشكل جيد مع البيانات المرصودة، فإن الفرضيات حول العملة والقيود مدعومة. إذا لم يتطابق النموذج بشكل جيد مع البيانات، فمن الممكن أن يكون قد حدّدت العملة أو القيد بشكل غير صحيح.^[5]

أنظمة التغذية المختلفة وفئات الحيوانات المفترسة

تنطبق نظرية البحث الأمثل عن الطعام على نطاق واسع على أنظمة التغذية في جميع أنحاء المملكة الحيوانية. بموجب هذه النظري، يمكن اعتبار أي كائن حي موضع اهتمام على أنه حيوان مفترس يتغذى على الفريسة. هناك فئات مختلفة من الجماعات المفترسة التي تنتمي إليها الكائنات الحية، وتتميز كل فئة باستراتيجيات مختلفة في البحث عن الطعام والافتراس.

• تهاجم الحيوانات المفترسة أعدادًا كبيرة من الفرائس طوال حياتها. تقتل فريستها إما مباشرة أو بعد وقت قصير من الهجوم. قد تأكل كل الفرائس أو جزء منها فقط. تشمل الحيوانات المفترسة الحقيقية النمور والأسود والحيتان وأسماك القرش والطيور الآكلة للبذور والنمل.^[7]
• لا تأكل حيوانات الرعي سوى جزء من فرائسها. إنها تؤذي الفريسة، لكنها نادرا ما تقتلها. تشمل حيوانات الرعي الظباء والماشية والبعوضيات.
• الطفيليات، مثل حيوانات الرعي، تأكل جزءًا فقط من فرائسها (مضيفها)، ولكن نادرًا ما تأكل الكائن الحي بأكمله. تقضي كل أو أجزاء كبيرة من دورة حياتها في / على مضيف واحد. هذه العلاقة الحميمة نموذجية للديدان الشريطية ومثقبيات الكبد والطفيليات النباتية، مثل آفة البطاطس.
• تعتبر شبيه الطفيليات نموذجية بشكل رئيسي للزنبار الطفيلي (غشائيات الأجنحة)، وبعض الذباب (ذوات الجناحين). يوضع البيض داخل يرقات مفصليات الأرجل الأخرى التي تفقس وتستهلك العائل من الداخل فتقتلها. هذه العلاقة غير العادية بين المفترس والمضيف هي نموذجية لحوالي 10٪ من جميع الحشرات. العديد من الفيروسات التي تهاجم الكائنات وحيدة الخلية (مثل العاثيات) هي أيضًا طفيليات ؛ تتكاثر داخل مضيف واحد يُقتل حتماً من المجموعة.

يمكن تفسير تحسين هذه الاستراتيجيات المختلفة للبحث عن الطعام والاصطياد من خلال نظرية البحث الأمثل. وفي كل حالة، هناك تكاليف وفوائد وقيود تحدد في النهاية القاعدة القرارية الأمثل التي يجب على المفترس اتباعها.

نموذج النظام الغذائي الأمثل

إحدى النسخ الكلاسيكية لنظرية البحث الأمثل عن الطعام هي نموذج النظام الغذائي الأمثل، والذي يُعرف أيضًا باسم نموذج اختيار الفريسة أو نموذج الطوارئ. في هذا النموذج، يواجه المفترس فريسة مختلفة ويقرر ما إذا كان سيأكل ما لديه أو يبحث عن فريسة أكثر ربحية. يتنبأ النموذج بأن الباحثين عن الطعام يجب أن يتجاهلوا الفرائس ذات الربحية المنخفضة عندما تكون الأخرى الأكثر ربحية موجودة بوفرة.^[8]

تعتمد ربحية الفريسة على عدة متغيرات بيئية. تُعرف الطاقة (E) المقدمة للمفترس من الفريسة بوحدة السعرات الحرارية. يُعرف وقت المعالجة (h) بالمدة الزمنية التي يستغرقها المفترس للتعامل مع الطعام، بدءًا من اللحظة التي يجد فيها المفترس الفريسة إلى اللحظة التي يتناول فيها الفريسة. تُعرف ربحية الفريسة بالتالي على أنها E/h. بالإضافة إلى ذلك، فإن وقت البحث (S) هو المدة الزمنية التي يستغرقها المفترس للعثور على الفريسة ويعتمد على وفرة الغذاء وسهولة تحديد موقعه.^[2] في هذا النموذج، تكون العملة هي كمية الطاقة التي تستهلك في الوحدة الزمنية وتشمل القيود القيم الفعلية لـ E وh وS، فضلاً عن حقيقة أن الفرائس يعثر عليها بتسلسل متتابع.

نموذج الاختيار بين الفريسة الكبيرة والصغيرة

باستخدام هذه المتغيرات، يمكن لنموذج النظام الغذائي الأمثل التنبؤ بكيفية اختيار المفترسين بين نوعين من الفريسة: الفريسة الكبيرة 1 ذات القيمة الحرارية E1 ووقت المعالجة h1، والفريسة الصغيرة 2 ذات القيمة الحرارية E2 ووقت المعالجة h2. ولكي يقوم المفترس بتحقيق أقصى معدل للحصول على الطاقة، يجب عليه أخذ ربحية النوعين من الفريسة بعين الاعتبار. إذا افترضنا أن الفريسة الكبيرة 1 أكثر ربحيةً من الفريسة الصغيرة 2، فإن E1/h1> E2/h2. وبالتالي، إذا وجد المفترس الفريسة الكبيرة 1، يجب أن يختار دائمًا تناولها بسبب ربحيتها الأعلى، ولا يجب أن يضيع وقته في البحث عن الفريسة الصغيرة 2. ومع ذلك، إذا وجد المفترس الفريسة الصغيرة 2، يجب عليه رفضها والبحث عن الفريسة الكبيرة 1 التي تكون أكثر ربحية، إلا إذا كان من المستحسن أن يستغرق الوقت الكبير الذي يستهلكه البحث عن الفريسة الكبيرة 1 كلفة عالية لا تستحق العناء. وبالتالي، يجب على المفترس أن يأكل الفريسة الصغيرة 2 فقط إذا كانت النسبة E2/h2> E1/(h1+S1)، حيث S1 هو وقت البحث عن الفريسة الكبيرة 1. ونظرًا لأنه دائمًا ما يكون من المرغوب اختيار تناول الفريسة الكبيرة 1، فإن الاختيار لتناول الفريسة الكبيرة 1 لا يعتمد على وفرة الفريسة الصغيرة 2. ولكن نظرًا لأن طول S1 (أي مدى صعوبة العثور على الفريسة الكبيرة 1) يعتمد منطقيًا على كثافة الفريسة الكبيرة 1، فإن الاختيار لتناول الفريسة الصغيرة 2 يتوقف على وفرة الفريسة الكبيرة 1.

النظم الغذائية العامة والمتخصصة

يتنبأ نموذج النظام الغذائي الأمثل أيضًا بأنه يجب على أنواع مختلفة من الحيوانات اعتماد نظم غذائية مختلفة بناءً على اختلافات في وقت البحث. هذه الفكرة هي تمديد لنموذج اختيار الفريسة الذي نوقش أعلاه. ويمكن إعادة ترتيب المعادلة E2/h2> E1/(h1+S1) لتعطي: S1> [(E1h2) / E2] - h1. تعطي هذه الصيغة المعادلة الحد الأدنى لمدة S1 التي يجب تجاوزها ليختار الحيوان تناول الفريسة 1 والفريسة 2.^[3] وتعرف الحيوانات التي تتجاوز مدة S1 الحد الأدنى على أنها شاملة ^{[الإنجليزية]} في الطبيعة، تتضمن الحيوانات الشاملة مجموعة واسعة من عناصر الغذاء في نظامها الغذائي.^[9] ومثال على الحيوان الشامل هو الفأر الذي يتناول مجموعة كبيرة من البذور والحبوب والمكسرات. على النقيض، فإن المفترسات التي لديها فترات بحث قصيرة نسبياً لا تزال أفضل حالًا باختيار تناول الفريسة 1 فقط. وتعرف هذه الأنواع من الحيوانات باسم الاختصاصيين ولديها أنظمة غذائية حصرية جدًا في الطبيعة.^[10] ومن الأمثلة على المتخصصين الكوالا، الذي يستهلك أوراق الأوكالبتوس فقط.^[11] بشكل عام، تعرض الحيوانات المختلفة عبر الفئات الوظيفية الأربعة للحيوانات المفترسة استراتيجيات تتراوح عبر سلسلة متصلة بين كونك متخصصًا ومتخصصًا. بالإضافة إلى ذلك، نظرًا لأن اختيار أكل الفريسة 2 يعتمد على وفرة الفريسة 1 (كما نوقش سابقًا)، إذا أصبحت الفريسة 1 نادرة جدًا بحيث وصلت S1 إلى الحد الأدنى، فيجب أن يتحول الحيوان من تناول الفريسة 1 حصريًا إلى أكل الفريسة 1 والفريسة 2.^[5] بعبارة أخرى، إذا أصبح الطعام داخل النظام الغذائي للمتخصص نادرًا جدًا، يمكن أن يتحول الاختصاصي أحيانًا إلى اختصاصي عام.

منحنيات الاستجابة الوظيفية

كما ذكرنا سابقًا، يعتمد مقدار الوقت الذي يستغرقه البحث عن عنصر الفريسة على كثافة الفريسة. تُظهر منحنيات الاستجابة الوظيفية ^{[الإنجليزية]} معدل التقاط الفريسة كدالة لكثافة الغذاء ويمكن استخدامها مع نظرية النظام الغذائي الأمثل للتنبؤ بسلوك البحث عن الطعام للحيوانات المفترسة. هناك ثلاثة أنواع مختلفة من منحنيات الاستجابة الوظيفية.

الشكل 2. ثلاثة أنواع من منحنيات الاستجابة الوظيفية. مقتبس من ستادون.

بالنسبة لمنحنى الاستجابة الوظيفية من النوع الأول، يزداد معدل التقاط الفريسة خطيًا مع كثافة الطعام. في كثافات الفريسة المنخفضة، يكون وقت البحث طويلاً. نظرًا لأن المفترس يقضي معظم وقته في البحث، فإنه يأكل كل فريسة يعثر عليها. مع زيادة كثافة الفريسة، يكون المفترس قادرًا على التقاط الفريسة بشكل أسرع وأسرع. عند نقطة معينة، يكون معدل التقاط الفريسة مرتفعًا جدًا، بحيث لا يضطر المفترس إلى أكل كل فريسة يصادفها. بعد هذه النقطة، يجب أن يختار المفترس فقط عناصر الفريسة ذات أعلى قيمة E/h.^[12]

بالنسبة لمنحنى الاستجابة الوظيفية من النوع الثاني، فإن معدل التقاط الفريسة يتسارع بشكل سلبي مع زيادة كثافة الطعام.^[13] هذا لأنه يفترض أن المفترس محدود بقدرته على معالجة الطعام. بمعنى آخر، مع زيادة كثافة الطعام، يزداد وقت المناولة. في بداية المنحنى، يزداد معدل التقاط الفريسة بشكل خطي تقريبًا مع كثافة الفريسة ولا يوجد وقت مناولة تقريبًا. مع زيادة كثافة الفريسة، يقضي المفترس وقتًا أقل وأقل في البحث عن الفريسة والمزيد والمزيد من الوقت في التعامل مع الفريسة. معدل التقاط الفريسة يزداد أقل فأقل، حتى يصل في النهاية إلى الهضاب. ارتفاع عدد الفرائس أساسًا "مستنقعات" المفترس.^[12]

منحنى الاستجابة الوظيفية من النوع الثالث هو دالة سينية. يزداد معدل التقاط الفريسة في البداية مع كثافة الفريسة بمعدل متسارع إيجابيًا، ولكن عند كثافات عالية يتغير إلى الشكل المتسارع سلبيًا، على غرار منحنى النوع الثاني. في كثافات الفريسة العالية (أعلى المنحنى)، تصطاد كل فريسة جديدة على الفور تقريبًا. يمكن للمفترس أن يكون انتقائيًا ولا يأكل كل فريسة يعثر عليها. لذلك، بافتراض وجود نوعين من الفرائس مع ربحية مختلفة وكلاهما بوفرة عالية، سيختار المفترس العنصر ذي E/h الأعلى. ومع ذلك، عند كثافات الفريسة المنخفضة (أسفل المنحنى)، يزيد معدل التقاط الفريسة بشكل أسرع من الخطي. هذا يعني أنه عندما يتغذى المفترس ويصبح نوع الفريسة مع E/h الأعلى أقل وفرة، سيبدأ المفترس في تبديل تفضيله إلى نوع الفريسة مع E/h الأقل، لأن هذا النوع سيكون أكثر وفرة نسبيًا. تُعرف هذه الظاهرة باسم تبديل الفريسة ^{[الإنجليزية]}.^[13]

التفاعل بين المفترس والفريسة

غالبًا ما يجعل التطور المشترك بين المفترس والفريسة من غير المناسب أن يستهلك المفترس عناصر معينة من الفريسة، نظرًا لأن العديد من الدفاعات المضادة للحيوانات المفترسة تزيد من وقت المناولة.^[14] تشمل الأمثلة ريشات النيص، واستساغة الضفدع السام وهضمه، والتمويه عند الحيوانات، وغيرها من سلوكيات تجنب الحيوانات المفترسة. كما تعتبر السموم من بين التحديات الأخرى التي تواجه الحيوانات المفترسة أثناء البحث عن الغذاء، حيث يمكن أن تكون موجودة في العديد من أنواع الفرائس المختلفة. ولتجنب تعرضها لمستويات خطيرة من السموم، تختلف نظم غذاء الحيوانات المفترسة بشكل كبير. وبالتالي، قد لا يكون النهج الذي يركز فقط على جمع الطاقة كافيًا لشرح سلوك الحيوانات المفترسة أثناء البحث عن الطعام في هذه الحالات.

نظرية القيمة الحدية والبحث الأمثل

الشكل 3. تظهر مبرهنة القيمة الحدودية بيانياً.

مبرهنة القيمة الحدودية ^{[الإنجليزية]}هي نوع من نموذج الأمثل الذي يطبق غالبًا على البحث الأمثل. تُستخدم هذه النظرية لوصف الموقف الذي يجب أن يقرر فيه الكائن الحي الذي يبحث عن طعام في رقعة متى يكون مناسبًا اقتصاديًا للمغادرة. عندما يكون الحيوان داخل رقعة، فإنه يواجه قانون الإنتاجية المتناقصة، حيث يصبح من الصعب العثور على فريسة مع مرور الوقت. قد يكون هذا بسبب نضوب الفريسة، أو أن الفريسة تبدأ في اتخاذ إجراءات مراوغة ويصبح من الصعب الإمساك بها، أو يبدأ المفترس في عبور طريقه أثناء البحث. يمكن إظهار قانون تناقص الغلة كمنحنى لكسب الطاقة لكل وقت يقضيه في رقعة (الشكل 3). يبدأ المنحنى بمنحدر حاد ويتراجع تدريجياً حيث يصعب العثور على الفريسة. تكلفة أخرى مهمة يجب مراعاتها هي وقت الرحلة بين البقع المختلفة وموقع التعشيش. يفقد الحيوان وقت البحث عن الطعام أثناء رحلته ويستهلك الطاقة من خلال حركته.^[2]

في هذا النموذج، العملة التي تحسين عادةً هي صافي ربح الطاقة لكل وحدة زمنية. القيود هي وقت التجول وشكل منحنى الإنتاجية المتناقصة. بيانياً، تُعطى العملة (صافي ربح الطاقة لكل وحدة زمنية) من خلال منحدر خط قطري يبدأ في بداية وقت التجول ويتقاطع مع منحنى تناقص الغلة (الشكل 3). من أجل تعظيم العملة، يريد المرء أن يكون الخط ذو المنحدر الأكبر الذي لا يزال يلامس المنحنى (خط المماس). يوفر المكان الذي يلامس فيه هذا الخط المنحنى قاعدة القرار المثلى لمقدار الوقت الذي يجب أن يقضيه الحيوان في رقعة قبل المغادرة.

أمثلة على نماذج نظرية البحث الأمثل عن الطعام عند الحيوانات

الشكل رقم 4. منحنى ربحية بلح البحر المحورة إلى اليمين. من ماير وإيرفينك.^[15]

نظرية البحث الأمثل عن الطعام عند صائد المحار

تقدم تغذية بلح البحر المحار مثالاً على كيفية استخدام نموذج النظام الغذائي الأمثل. يتغذى صائدو المحار على بلح البحر ويفتح الأصداف بمناقيرها. القيود المفروضة على هذه الطيور هي خصائص أحجام بلح البحر المختلفة. في حين أن بلح البحر الكبير يوفر طاقة أكبر من بلح البحر الصغير، إلا أنه يصعب تكسير بلح البحر الكبير بسبب أصدافه السميكة. هذا يعني أنه في حين أن بلح البحر الكبير يحتوي على محتوى طاقة أعلى (E)، إلا أنه يمتلك أيضًا وقتًا أطول للمناولة (h). تحتستب ربحية أي بلح البحر على أنها E/h. يجب على صائدي المحار أن يقرروا حجم بلح البحر الذي سيوفر غذاءً كافياً يفوق التكلفة والطاقة اللازمتين لفتحه.^[2] في دراستهم، حاول ماير وإيرفينك صياغة هذا القرار من خلال رسم بياني للربحية النسبية لبلح البحر مختلف الأحجام. لقد توصلوا إلى منحنى على شكل جرس، مما يشير إلى أن بلح البحر متوسط الحجم كان الأكثر ربحية. ومع ذلك، فقد لاحظوا أنه إذا رفض صائد المحار الكثير من بلح البحر الصغير، فإن الوقت الذي يستغرقه البحث عن بلح البحر المناسب التالي يزداد بشكل كبير. حولت هذه الملاحظة منحنى الجرس إلى اليمين (الشكل 4). ومع ذلك، في حين أن هذا النموذج تنبأ بأن صائدي المحار يجب أن يفضلوا بلح البحر بنسبة 50-55 مم، أظهرت البيانات المرصودة أن صائدي المحار يفضلون في الواقع بلح البحر من 30-45 مم. أدرك ماير وإرفينك بعد ذلك أن تفضيل حجم بلح البحر لا يعتمد فقط على ربحية الفريسة، ولكن أيضًا على كثافة الفريسة. بعد احتساب ذلك، وجدوا اتفاقًا جيدًا بين تنبؤ النموذج والبيانات المرصودة.^[15]

نظرية البحث الأمثل عن الطعام عند الزرزور

الشكل 5. إذا كان الزرزور يضاعف صافي معدل كسب الطاقة، فإن وقت الرحلة الأطول ينتج عنه حمل أمثل أكبر. من كريبس وديفيز.^[5]

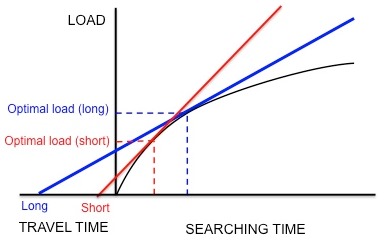
يقدم سلوك البحث عن الطعام للزرزور الأوروبي، مثالًا على كيفية استخدام نظرية القيمة الحدية لنمذجة البحث الأمثل. الزرزور يتركون أعشاشهم ويسافرون إلى أماكن الطعام بحثًا عن طيثارية جلدية من اليرقات لإعادتها إلى صغارهم. يجب أن تحدد الزرزور العدد الأمثل لعناصر الفريسة لاستعادتها في رحلة واحدة (أي حجم الحمل الأمثل). عندما يتغذى الزرزور داخل منطقة معينة، فإنه يواجه تحديات عديدة، فمن بين هذه التحديات تناقص الغلة المتاحة للأكل. ويرجع هذا التناقص إلى قدرة الزرزور على الاحتفاظ فقط بعدد محدود من اليرقات الجلدية في منقاره، مما يؤدي إلى تقليل سرعة الحصول على المزيد من اليرقات. وتُعد القيود هنا شكلًا من أشكال التحديات التي تواجه الزرزور، وتتمثل هذه القيود في تناقص الغلة المتاحة ووقت الرحلة اللازم للذهاب والعودة من العش إلى المنطقة المخصصة للتغذية.^[3] وباستخدام العملة المعتمدة هنا، وهي صافي ربح الطاقة لكل وحدة زمنية، يمكن توقع الحمل الأمثل من الغذاء الممكن الحصول عليه، من خلال رسم خط مماس لمنحنى تناقص الغلة المتوفرة للحصول على الطعام. وقد تم مناقشة هذه الأفكار سابقًا في (الشكل 3).

أراد (كاسيلنيك وآخرون) تحديد ما إذا كانت هذه الأنواع تعمل بالفعل على تحسين صافي كسب الطاقة لكل وحدة زمنية كما هو مفترض.^[16] لقد صمموا تجربة درب فيها الزرزور على جمع الدودة القشرية ^{[الإنجليزية]} من وحدة تغذية صناعية على مسافات مختلفة من العش. أنشأ الباحثون بشكل مصطنع منحنى ثابتًا لتناقص العوائد للطيور عن طريق إسقاط ديدان الوجبة على فترات متتالية أطول وأطول. استمرت الطيور في جمع ديدان الوجبة أثناء تقديمها، حتى وصلت إلى الحمل "الأمثل" وعادت إلى المنزل. كما يوضح الشكل 5، إذا كان الزرزور يضاعف صافي كسب الطاقة لكل وحدة زمنية، فإن وقت الرحلة القصير سيتنبأ بحمل مثالي صغير وسيتنبأ وقت الرحلة الطويل بحمل أمثل أكبر. بالاتفاق مع هذه التوقعات، وجد كاسيلنيك أنه كلما زادت المسافة بين العش والمغذي الاصطناعي، زاد حجم الحمولة. بالإضافة إلى ذلك، فإن أحجام الحمل الملحوظة تتوافق من الناحية الكمية بشكل وثيق جدًا مع تنبؤات النموذج. نماذج أخرى تعتمد على عملات مختلفة، مثل الطاقة المكتسبة لكل طاقة مستهلكة (أي كفاءة الطاقة)، فشلت في التنبؤ بأحجام الأحمال المرصودة بدقة. وهكذا، خلص كاسيلنيك إلى أن الزرزور يزيد من صافي كسب الطاقة لكل وحدة زمنية. لم يدحض هذا الاستنتاج في التجارب اللاحقة.^[17][18]

نظرية البحث الأمثل عن الطعام عند النحل

يقدم النحل العامل مثالًا آخر على استخدام نظرية القيمة الحدية في نمذجة سلوك البحث الأمثل. يتغذى النحل من زهرة إلى زهرة لجمع الرحيق لإعادته إلى الخلية. في حين أن هذا الموقف مشابه لوضع الزرزور، فإن القيود والعملة تختلف في الواقع بالنسبة للنحل.

لا تعاني النحلة من تناقص الغلة بسبب نضوب الرحيق أو أي خاصية أخرى للزهور نفسها. يزداد إجمالي كمية الرحيق الطعامية خطيًا مع الوقت الذي يقضيه في الرقعة. ومع ذلك، فإن وزن الرحيق يضيف تكلفة كبيرة لرحلة النحلة بين الزهور ورحلتها إلى الخلية. أظهر وولف وشميد-همبل، من خلال وضع أوزان متفاوتة تجريبياً على ظهور النحل، أن تكلفة الرحيق الثقيل كبيرة جدًا لدرجة أنها تقصر من عمر النحل.^[19] كلما كان عمر النحلة العاملة أقصر، قل الوقت الإجمالي الذي يجب أن تساهم به في مستعمرتها. وبالتالي، هناك منحنى الإنتاجية المتناقصة لصافي عائد الطاقة الذي تتلقاه الخلية عندما تجمع النحلة المزيد من الرحيق خلال رحلة واحدة.

تؤثر تكلفة الرحيق الثقيل أيضًا على العملة التي يستخدمها النحل. على عكس الزرزور في المثال السابق، يزيد النحل من كفاءة الطاقة (الطاقة المكتسبة لكل طاقة مستهلكة) بدلاً من المعدل الصافي لكسب الطاقة (صافي الطاقة المكتسبة في كل مرة). وذلك لأن الحمل الأمثل الذي تُوقع من خلال تعظيم صافي معدل اكتساب الطاقة ثقيل جدًا بالنسبة للنحل ويقصر من العمر الافتراضي، مما يقلل من إنتاجيتها الإجمالية للخلية، كما هو موضح سابقًا. من خلال زيادة كفاءة الطاقة إلى الحد الأقصى، يكون النحل قادرًا على تجنب إنفاق الكثير من الطاقة لكل رحلة ويكون قادرًا على العيش لفترة طويلة بما يكفي لزيادة إنتاجية حياته لخلته.^[5] في ورقة أخرى، أظهر وشميد-همبل أن العلاقة الملحوظة بين حجم الحمولة ووقت الرحلة ترتبط ارتباطًا وثيقًا بالتنبؤات القائمة على تعظيم كفاءة الطاقة، ولكنها غير مرتبطة بشكل كبير بالتنبؤات القائمة على تعظيم صافي معدل اكتساب الطاقة.^[20]

نظرية البحث الأمثل عن الطعام عند أسماك الشمس

شُرح طبيعة اختيار فريسة اثنين من أسماك الشمس الأمريكي (الكرابي الأبيض والبلوجيل) كنموذج يدمج استراتيجيات البحث الأمثل عن الغذاء المثلى بواسطة ماناتونج وأسايدا.^[21] حُلل حقل الرؤية للسمك الباحث بالنظر إلى المسافة التفاعلية بالتفصيل لتقدير عدد لقاءات الفريسة لكل رحلة بحث. قورنت المسافات التفاعلية المتوقعة مع البيانات التجريبية. حُسبت التكلفة الحرارية المرتبطة بسلوك السمك في البحث عن الغذاء بناءً على تسلسل الأحداث التي تحدث لكل فريسة تستهلك. أشارت مقارنات الوفرة النسبية لأنواع الفريسة وفئات الحجم في المعدة إلى بيئة البحيرة إلى أن الكرابي الأبيض والبلوجيل (الطول<100 مم) يختاران الفريسة باستخدام استراتيجية تحسين الطاقة. في معظم الحالات، اختار السمك حصريًا الدافنيا الكبيرة وتجاهل أنواع الفريسة الهاربة (السيكلوبس والديابتوميدس) والكلادوسيرا الصغيرة. يعود هذا الاختيار الى تفادي السمك للفرائس التي لها قدرات عالية في التهرب حتى لو كانت ذات محتوى طاقوي عالي وتحويل هذا الاختيار إلى اختيار مثالي من خلال معدلات نجاح الصيد. إن اعتبارات الطاقة والنظام البصري، بالإضافة إلى قدرة الباحث عن الغذاء على اصطياد الفريسة، هي المحددات الرئيسية للاختيار الفريسي لكل من الكرابي الأبيض والبلوجيل ذات الحجم الكبير واللذان لا يزالان في مراحل الأكل الهامشي.

نقد نظرية البحث الأمثل عن الطعام وقيودها

على الرغم من أن العديد من الدراسات، مثل تلك المذكورة في الأمثلة أعلاه، توفر دعمًا كميًا لنظرية البحث الأمثل عن الطعام وتثبت فائدتها، فقد تلقى النموذج انتقادات بشأن صدقه وقيوده.

أولاً، تعتمد نظرية البحث الأمثل عن الطعام على افتراض أن الانتقاء الطبيعي سيعمل على تحسين استراتيجيات البحث عن الطعام للكائنات الحية. ومع ذلك، فإن الانتقاء الطبيعي ليس قوة كاملة تنتج تصميمات مثالية، بل عملية اختيار سلبية للسمات القائمة على الجينات التي تزيد من النجاح التناسلي للكائنات الحية. بالنظر إلى أن علم الوراثة يتضمن تفاعلات بين الموقع وإعادة التركيب والتعقيدات الأخرى، فلا يوجد ضمان بأن الانتقاء الطبيعي يمكنه تحسين معلمة سلوكية معينة.^[22]

بالإضافة إلى ذلك، تفترض نظرية البحث الأمثل عن الطعام أيضًا أن سلوكيات البحث عن الطعام يمكن تشكيلها بحرية عن طريق الانتقاء الطبيعي، لأن هذه السلوكيات مستقلة عن الأنشطة الأخرى للكائن الحي.^[22] ومع ذلك، نظرًا لأن الكائنات الحية عبارة عن أنظمة متكاملة، وليست مجاميع ميكانيكية للأجزاء، فإن هذا ليس هو الحال دائمًا. على سبيل المثال، قد تؤدي الحاجة إلى تجنب الحيوانات المفترسة إلى تقييد الباحثين عن الطعام لإطعام أقل من المعدل الأمثل. وبالتالي، قد لا تحسن سلوكيات البحث عن الطعام للكائن الحي كما يتوقع نظرية البحث الأمثل عن الطعام، لأنها ليست مستقلة عن السلوكيات الأخرى.^[23]

تشكل الدقة مشكلة إضافية في نموذج البحث الأمثل عن الطعام، حيث يمكن أن يوفر هذا النموذج توقعات نظرية دقيقة حول سلوك الحيوانات المفترسة بناءً على فرضيات معينة حول العملة والقيود. ومع ذلك، في الواقع، يصعب تحديد المتغيرات الأساسية للنموذج مثل نوع الفريسة ومعدلات المواجهة وحتى الرقعة التي تراها الحيوانات المفترسة. وبالتالي، وعلى الرغم من أن متغيرات نموذج البحث الأمثل عن الطعام يمكن أن تبدو متسقة من الناحية النظرية، فإنها في الواقع يصعب قياسها ويمكن أن تكون تعسفية.^[22] وبالتالي، يجب أن يتم التفكير في النموذج النظري للبحث الأمثل عن الطعام بعناية وتوظيفه بشكل مناسب في دراسات السلوك الفعلية للحيوانات المفترسة في الطبيعة.

علاوة على ذلك، يتمحور افتراض نظرية البحث الأمثل عن الطعام حول زيادة لياقة الحيوانات المفترسة إلى أقصى حد ممكن. ومع ذلك، فإن الدراسات التي تستخدم هذه النظرية غالبًا ما تقتصر على الارتباطات بين سلوك البحث عن الطعام الملاحظ والمتوقع، دون اختبار ما إذا كان سلوك الحيوانات المفترسة يؤدي فعلاً إلى زيادة لياقتها الإنجابية. وبالتالي، يمكن أن يكون من الممكن في بعض الحالات عدم وجود علاقة بين عوائد البحث عن الطعام ونجاح التكاثر.^[22] ومن دون احتساب هذا الاحتمال، تبقى الدراسات التي تستخدم نظرية البحث الأمثل عن الطعام غير مكتملة وتفتقر إلى القدرة على معالجة واختبار النقطة الرئيسية للنظرية.

تشكل واحدة من أهم الانتقادات لنظرية البحث الأمثل عن الطعام هو أنها قد لا تكون قابلة للاختبار بشكل حقيقي. ينشأ هذا التحدي عندما يتعارض تنبؤ النموذج مع الملاحظات الفعلية. وبسبب إمكانية إدخال تعديلات لا نهاية لها على النموذج، فإنه من الممكن أن يظل النموذج الأمثل قابلاً للتطبيق بشكل دائم.^[22] وهذا يمثل تحديًا كبيرًا للباحثين في صياغة النموذج الخاص بهم بحيث يتناسب مع الملاحظات الفعلية، بدلاً من تعديل الملاحظات الفعلية لتتناسب مع نموذجهم. وبالتالي، يصعب على الباحثين اختبار فرضياتهم حول سلوك البحث عن الطعام للحيوانات بدقة.

نظرية البحث الأمثل عن الطعام في علم الآثار

استخدمت نظرية البحث الأمثل عن الطعام للتنبؤ بسلوك الحيوان عند البحث عن الطعام، ولكن يمكن استخدامها أيضًا للبشر (على وجه التحديد أعضاء مجتمع الجمع والالتقاط). يوفر الغذاء الطاقة ولكنه يكلف الطاقة للحصول على هذا المجتمع. يجب أن توفر استراتيجية هذه النظرية أكبر فائدة بأقل تكلفة - فهي توازن بين القيمة الغذائية والطاقة المطلوبة. كما تعتبر عملة نظرية البحث الأمثل عن الطعام هي الطاقة لأنها مكون أساسي للكائنات الحية، ولكنها أيضًا تمثل سقوط النظرية فيما يتعلق بعلم الآثار.^[24] تفترض النظرية أن السلوك يتأثر إلى حد ما بالتركيب الجيني. ومع ذلك، قد يكون من الصعب قبول ذلك فيما يتعلق بالحيوانات المعقدة التي تتمتع بمرونة سلوكية عالية.^[25]

لا يمكن التنبؤ بالسلوك البشري دائمًا عند استخدام نظرية البحث الأمثل عن الطعام - يمكن مجتمع الجمع والالتقاط لأهداف تتعلق بالطقوس أ الولائم - اختيار لعبة لا تفيد الطاقة، ولكنها ستفيد الاحتياجات الأخرى.^[24] غالبًا ما تتغير أهداف وعملات البشر بسبب المرونة السلوكية. يمكن أن تحدث هذه التغييرات على مدى فترة طويلة، على مدار موسم أو أثناء الصيد. لذلك يجب أن تكون نظرية البحث الأمثل عن الطعام أكثر تعقيدًا وأن تقدم المزيد من الأهداف والقيود لمطابقة عمليات صنع القرار المعقدة التي يستخدمها البشر.^[26] علاوة على ذلك، يمكن أن تتأثر عمليات صنع القرار بالخبرات طويلة المدى وقصيرة المدى ويمكن لهذه التجارب أن تؤثر بشكل أكبر على الآخرين.^[26]

يمكن القول إن نظرية البحث الأمثل عن الطعام قد ساهمت في تطوير فهمنا للسلوكيات الإنسانية والأنماط السلوكية القديمة التي توجد في السجل الآثاري. وفي نفس الوقت، قدمت هذه النظرية نظرة أفضل على تكلفة وفوائد الموارد المختلفة، مما يساعد في فهم أفضل لسلوكيات الحيوانات والبشر على حد سواء. وبالتالي، فإن نظرية البحث الأمثل عن الطعام تعد أداة قيمة للعلماء في دراسة السلوك الحيواني والإنساني وفي فهم التفاعلات بين الكائنات الحية وبيئتها.^[24]

المراجع

1. Werner، E. E.؛ Hall، D. J. (1974). "Optimal Foraging and the Size Selection of Prey by the Bluegill Sunfish (Lepomis macrochirus)". Ecology. ج. 55 ع. 5: 1042. DOI:10.2307/1940354. JSTOR:1940354.
2. Sinervo, Barry (1997). "Optimal Foraging Theory: Constraints and Cognitive Processes" نسخة محفوظة 23 November 2015 على موقع واي باك مشين., pp. 105–130 in Behavioral Ecology. University of California, Santa Cruz.
3. Krebs, J. R. and Davies, N. B. (1989) An Introduction to Behavioral Ecology. 4th ed. Oxford: Blackwell Scientific Publications.^{[بحاجة لمُعرِّف الكتاب][بحاجة لرقم الصفحة]}
4. Verlinden، C.؛ Wiley، R. H. (1989). "The constraints of digestive rate: An alternative model of diet selection". Evolutionary Ecology. ج. 3 ع. 3: 264. DOI:10.1007/BF02270727. S2CID:46608348.
5. Krebs, J. R. and Davies, N. B. (1989) An Introduction to Behavioral Ecology. 4th ed. Oxford: Blackwell Scientific Publications.^{[بحاجة لمُعرِّف الكتاب][بحاجة لرقم الصفحة]}
6. Parker، G. A.؛ Smith، J. M. (1990). "Optimality theory in evolutionary biology". Nature. ج. 348 ع. 6296: 27. Bibcode:1990Natur.348...27P. DOI:10.1038/348027a0.
7. Cortés، E.؛ Gruber، S. H.؛ Cortes، E. (1990). "Diet, Feeding Habits and Estimates of Daily Ration of Young Lemon Sharks, Negaprion brevirostris (Poey)". Copeia. ج. 1990 ع. 1: 204–218. DOI:10.2307/1445836. JSTOR:1445836.
8. Stephens, D.W., Brown, J.S., and Ydenberg, R.C. (2007). Foraging: Behavior and Ecology. Chicago: University of Chicago Press.^{[بحاجة لمُعرِّف الكتاب][بحاجة لرقم الصفحة]}
9. Pulliam, H. Ronald (1974). "On the theory of optimal diets". American Naturalist. ج. 108 ع. 959: 59–74. DOI:10.1086/282885. JSTOR:2459736. S2CID:8420787.
10. Pulliam, H. Ronald (1974). "On the theory of optimal diets". American Naturalist. ج. 108 ع. 959: 59–74. DOI:10.1086/282885. JSTOR:2459736.
11. Shipley، L. A.؛ Forbey، J. S.؛ Moore، B. D. (2009). "Revisiting the dietary niche: When is a mammalian herbivore a specialist?". Integrative and Comparative Biology. ج. 49 ع. 3: 274–290. DOI:10.1093/icb/icp051. PMID:21665820.
12. Jeschke، J. M.؛ Kopp، M.؛ Tollrian، R. (2002). "Predator Functional Responses: Discriminating Between Handling and Digesting Prey". Ecological Monographs. ج. 72: 95–112. DOI:10.1890/0012-9615(2002)072[0095:PFRDBH]2.0.CO;2.
13. Staddon, J.E.R. "Foraging and Behavioral Ecology." Adaptive Behavior and Learning. First Edition ed. Cambridge UP, 1983.^{[بحاجة لمُعرِّف الكتاب][بحاجة لرقم الصفحة]}
14. Boulding، Elizabeth Grace (1984). "Crab-resistant features of shells of burrowing bivalves: decreasing vulnerability by increasing handling time". Journal of Experimental Marine Biology and Ecology. ج. 76 ع. 3: 201–23. DOI:10.1016/0022-0981(84)90189-8.
15. Meire، P. M.؛ Ervynck، A. (1986). "Are oystercatchers (Haematopus ostralegus) selecting the most profitable mussels (Mytilus edulis)?" (PDF). Animal Behaviour. ج. 34 ع. 5: 1427. DOI:10.1016/S0003-3472(86)80213-5. مؤرشف من الأصل (PDF) في 2022-07-09.
16. Kacelnik، A. (1984). "Central Place Foraging in Starlings (Sturnus vulgaris). I. Patch Residence Time". The Journal of Animal Ecology. ج. 53 ع. 1: 283–299. DOI:10.2307/4357. JSTOR:4357.
17. Bautista، L.M.؛ Tinbergen، J.M.؛ Wiersma، P.؛ Kacelnik، A. (1998). "Optimal foraging and beyond: how starlings cope with changes in food availability" (PDF). The American Naturalist. ج. 152 ع. 4: 221–38. DOI:10.1086/286189. JSTOR:10.1086/286189. PMID:18811363. مؤرشف من الأصل (PDF) في 2022-07-09.
18. Bautista، L.M.؛ Tinbergen، J.M.؛ Kacelnik، A. (2001). "To walk or to fly? How birds choose among foraging modes". Proc. Natl. Acad. Sci. USA. ج. 98 ع. 3: 1089–94. Bibcode:2001PNAS...98.1089B. DOI:10.1073/pnas.98.3.1089. JSTOR:3054826. PMC:14713. PMID:11158599.
19. Wolf، T. J.؛ Schmid-Hempel، P. (1989). "Extra Loads and Foraging Life Span in Honeybee Workers". The Journal of Animal Ecology. ج. 58 ع. 3: 943. DOI:10.2307/5134. JSTOR:5134.
20. Schmid-Hempel، P.؛ Kacelnik، A.؛ Houston، A. I. (1985). "Honeybees maximize efficiency by not filling their crop". Behavioral Ecology and Sociobiology. ج. 17: 61–66. DOI:10.1007/BF00299430.
21. Manatunge، Jagath؛ Asaeda، Takashi (1998). "Optimal foraging as the criteria of prey selection by two centrarchid fishes". Hydrobiologia. ج. 391 ع. 1: 221–39. DOI:10.1023/a:1003519402917. S2CID:24808827.
22. Gray, Russell D. "Faith and Foraging: A Critique of the "Paradigm Argument from Design"" p. 198 in Foraging Behavior. Ed. Alan C. Kamil, John R. Krebs, and H. Robald Pulliam. New York: Plenum^{[بحاجة لمُعرِّف الكتاب]}
23. Pierce, G. J.؛ Ollason, J. G. (1987). "Eight reasons why optimal foraging theory is a complete waste of time" (PDF). Oikos. ج. 49 ع. 1: 111–18. DOI:10.2307/3565560. JSTOR:3565560. مؤرشف من الأصل (PDF) في 2022-12-24.
24. Keene, ARTHUR S. (1 Jan 1983), Moore; Keene, ARTHUR S. (eds.), "6 - Biology, Behavior, and Borrowing: A Critical Examination of Optimal Foraging Theory in Archaeology", Archaeological Hammers and Theories (بالإنجليزية), Academic Press, pp. 137–155, ISBN:978-0-12-505980-0, Archived from the original on 2022-11-30, Retrieved 2022-11-30
25. Shennan، Stephen (1 أبريل 2002). "Archaeology and evolutionary ecology". World Archaeology. ج. 34 ع. 1: 1–5. DOI:10.1080/00438240220134223. ISSN:0043-8243. PMID:16475304. مؤرشف من الأصل في 2022-11-30.
26. Mithen, Steven J. (1 Mar 1988). "Modeling hunter-gatherer decision making: complementing optimal foraging theory". Human Ecology (بالإنجليزية). 17 (1): 59–83. DOI:10.1007/BF01047652. ISSN:1572-9915. Archived from the original on 2022-12-11.

• بوابة علم الأحياء
• بوابة علم الأحياء التطوري
• بوابة علم البيئة
• بوابة علم الحيوان