Enerxía cinético

Enerxía cinético
forma d'enerxía
enerxía mecánico, propiedá física escalar y cantidá física

En física, la enerxía cinético d'un cuerpu ye aquella enerxía que tien por cuenta del so movimientu. Defínese como'l trabayu necesariu p'acelerar un cuerpu d'una masa determinao dende'l reposu hasta la velocidá indicada. Una vegada consiguida esta enerxía mientres l'aceleración, el cuerpu caltién la so enerxía cinético sacantes camude la so velocidá. Por que el cuerpu torne al so estáu de reposu ríquese un trabayu negativu de la mesma magnitú que la so enerxía cinético. Suel embrivise con lletra Y_- o Y₊ (dacuando tamién T o K).

Introducción

L'axetivu cinéticu» nel nome enerxía vien de l'antigua pallabra griega κίνησις kinēsis, que significa «movimientu». Los términos enerxía cinético y trabayu y el so significáu científicu provienen del sieglu XIX.

El principiu de la mecánica clásica que ${\displaystyle Y\propto mv^{2}}$ foi desenvueltu per primer vegada por Gottfried Leibniz y Daniel Bernoulli , que describe la enerxía cinético como la fuercia vivo o vis viva. Willem 's Gravesande de los Países Baxos apurrió evidencia esperimental d'esta rellación. Al cayer los pesos de distintos altores nun bloque de magre, Gravesande determinó que la fondura de penetración ye proporcional al cuadráu de la velocidá d'impautu. Émilie du Châtelet reconoció les implicaciones del esperimentu y publicó una esplicación.

Les primeres conocencies d'eses idees pueden ser atribuyíos a Gaspard Coriolis quien en 1829 publicó un artículu tituláu Du Calcul de l'Effet des Machines esbozando les matemátiques de la enerxía cinético. El términu enerxía cinético deber a William Thomson más conocíu como Lord Kelvin en 1849.

Esisten delles formes d'enerxía como la enerxía química, el calor, la radiación electromagnético, la enerxía nuclear, les enerxíes gravitacional, llétrica, elástica, etc, toes elles pueden ser arrexuntaes en dos tipos: la enerxía potencial y la enerxía cinético.

La enerxía cinético pue ser entendida meyor con exemplos que demuestren cómo esta se tresforma d'otros tipos d'enerxía y a otros tipos d'enerxía. Por casu un ciclista quier usar la enerxía química que-y apurrió'l so comida p'acelerar la so bicicleta a una velocidá escoyida. La so velocidá puede caltenese ensin enforma trabayu, sacante pola resistencia aerodinámica y el resfregón mecánicu. La enerxía química ye convertida nuna enerxía de movimientu, conocida como enerxía cinético, pero'l procesu nun ye dafechu eficiente una y bones el ciclista tamién produz calor.

La enerxía cinético en movimientu de la bicicleta y el ciclista pueden convertise n'otres formes. Por casu, el ciclista puede atopar una cuesta lo suficientemente alta pa xubir, asina que tien de cargar la bicicleta hasta'l visu. La enerxía cinético hasta agora usada convertiríase n'enerxía potencial gravitatoria que puede lliberar llanzándose cuesta abaxo pel otru llau de la llomba. Alternativamente'l ciclista puede coneutar una dínamo a una de les sos ruedes y asina xenerar enerxía llétrica nel descensu. La bicicleta podría tar viaxando más adulces nel final de la llomba porque muncha d'esa enerxía foi esviada en faer enerxía llétrica. Otra posibilidá podría ser que'l ciclista aplique los sos frenos y nesi casu la enerxía cinético taría estenándose al traviés del resfregón n'enerxía calórica.

Como cualquier magnitú física que seya función de la velocidá, la enerxía cinético d'un oxetu non solo depende de la naturaleza interna d'esi oxetu, tamién depende de la rellación ente l'oxetu y l'observador (en física un observador ye formalmente definíu por una clase particular de sistema de coordenaes llamáu sistema inercial de referencia). Magnitúes físiques como esta son llamaes invariantes. La enerxía cinético esta co-alcontrada col oxetu y atribuyíu a esi campu gravitacional.

El cálculu de la enerxía cinético realizar de distintes formes según úsese la mecánica clásica, la mecánica relativista o la mecánica cuántica. La manera correuta de calcular la enerxía cinético d'un sistema depende del so tamañu, y la velocidá de les partícules que la formen. Asina, si l'oxetu mover a una velocidá muncho más baxa que la velocidá de la lluz, la mecánica clásica de Newton va ser abonda pa los cálculos; pero si la velocidá ye cercana a la velocidá de la lluz, la teoría de la relatividá empieza a amosar diferencies significatives na resultancia y tendría de ser usada. Si'l tamañu del oxetu ye más pequeñu, esto ye, de nivel sub-atómicu, la mecánica cuántica ye más apropiada.

Esta enerxía degrádase y caltiénse en cada tresformamientu, perdiendo capacidá de realizar nuevos tresformamientos, pero la enerxía nun puede ser creada nin destruyida, solo tresformada, polo que la suma de toles enerxíes nel universu ye siempres constante. Un oxetu va perder enerxía nun tresformamientu, pero esa perda d'enerxía dirá parar a otru sitiu, por casu puede tresformase en calor.

Enerxía cinética en mecánica clásica

Enerxía cinética en distintos sistemes de referencia

Como diximos, na mecánica clásica, la enerxía cinético d'una masa puntual depende de la so masa ${\displaystyle m}$ y los sos componentes del movimientu. Espresar en Joule (J). 1 J = 1 kg·m²/s². Estos son descritos pola velocidá ${\displaystyle v}$ de la masa puntual, asina: ${\displaystyle Y_{c}={\frac {mv^{2}}{2}}}$

Nun sistema de coordenaes especial, esta espresión tien les siguientes formes:

• Coordenaes cartesianes (x, y, z):

${\displaystyle Y_{c}={1 \over 2}m({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2})}$

• Coordenaes polares (${\displaystyle r,\phi }$):

${\displaystyle Y_{c}={\frac {1}{2}}m\left({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2}\right)}$

• Coordenaes cilíndriques (${\displaystyle r,\phi ,z}$):

${\displaystyle Y_{c}={\frac {1}{2}}m\left({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2}+{\dot {z}}^{2}\right)}$

• Coordenaes esfériques (${\displaystyle r,\phi ,\theta }$):

${\displaystyle Y_{c}={\frac {1}{2}}m\left(r^{2}\left[{\dot {\theta }}^{2}+{\dot {\varphi }}^{2}\sin ^{2}\theta \right]+{\dot {r}}^{2}\right)}$

Con eso'l significáu d'un puntu nuna coordenada y el so cambéu temporal descríbese como la derivada temporal de la so desplazamientu:

${\displaystyle {\dot {x}}={\frac {\mathrm {d} x}{\mathrm {d} t}}={\frac {\mathrm {d} }{\mathrm {d} t}}x(t)}$

Nun formalismu hamiltoniano nun se trabaya con eses componentes del movimientu, esto ye cola so velocidá, sinón cola so impulsu ${\displaystyle p}$ (cambéu na cantidá de movimientu). En casu d'usar componentes cartesianes llogramos:

${\displaystyle Y_{c}={\frac {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}{2m}}}$

Enerxía cinética de sistemes de partícules

Pa una partícula, o pa un sólidu ríxidu que non esti rotando, la enerxía cinético cai a cero cuando'l cuerpu para. Sicasí, pa sistemes que contienen munchos cuerpos con movimientos independientes, qu'exercen fuercies ente ellos y que pueden (o non) tar rotando, esto nun ye del tou ciertu. Esta enerxía ye llamada 'enerxía interna'. La enerxía cinético d'un sistema en cualquier intre de tiempu ye la suma simple de les enerxíes cinétiques de les mases, incluyendo la enerxía cinético de la rotación.

Un exemplu d'esto pue ser el Sistema Solar. Nel centru de mases del sistema solar, el Sol ta (cuasi) estacionariu, pero los planetes y planetoides tán en movimientu sobre él. Asina nun centru de mases estacionariu, la enerxía cinético ta entá presente. Sicasí, recalcular la enerxía de distintos marcos puede ser aburrible, pero hai un trucu. La enerxía cinético d'un sistema de distintos marcos inerciales puede calculase como la simple suma de la enerxía nun marcu con centru de mases y añader na enerxía'l total de les mases de los cuerpos que se mueven con velocidá relativa ente los dos marcos.

Esto puédese demostrar fácilmente: seya V la velocidá relativa nun sistema k d'un centru de mases i:

${\displaystyle Y_{c}=\int {\frac {\mathbf {v} ^{2}}{2}}dm=\int {\frac {({\bar {\mathbf {v} }}+\mathbf {V} )^{2}}{2}}dm=\underbrace {\int {\frac {{\bar {\mathbf {v} }}^{2}}{2}}dm} _{Y_{c,int}}+\underbrace {\mathbf {V} \int {\bar {\mathbf {v} }}dm} _{\mathbf {V} \cdot \mathbf {P} =0}+\underbrace {{\frac {V^{2}}{2}}\int dm} _{Y_{c,Cn}}}$

Onde:

${\displaystyle Y_{c,int}\,}$, ye la enerxía cinético interna respectu al centru de mases d'esi sistema :${\displaystyle \mathbf {P} }$

ye'l momentu respeuto al centru de mases, que resulta ser cero pola definición de centru de mases.

${\displaystyle M\,}$, ye la masa total.

Polo que la espresión anterior puede escribise a cencielles como:^[1]

${\displaystyle Y_{c}=\overbrace {Y_{c,int}} ^{Y_{rot}}+M{\frac {V^{2}}{2}}=Y_{rot}+Y_{tres}}$

Onde puede trate más claramente que enerxía cinético parcial d'un sistema puede descomponese nel so enerxía cinético de traslación y la enerxía de rotación alredor del centru de mases. La enerxía cinético d'un sistema entós depende del Sistema de referencia inercial y ye más baxu con respectu al centru de mases reverencial, por casu, nun sistema de referencia en que'l centru de mases seya estacionariu. En cualesquier otru sistema de referencia hai una enerxía cinético adicional correspondiente a la masa total que se mueve a la velocidá del centru de mases.

Enerxía cinética d'un sólidu ríxidu en rotación

Pa un sólidu ríxidu que ta rotando puede descomponese la enerxía cinético total como dos sumes: la enerxía cinético de traslación (que ye l'asociada al desplazamientu del centru de masa del cuerpu al traviés del espaciu) y la enerxía cinético de rotación (que ye l'asociada al movimientu de rotación con cierta velocidá angular). La espresión matemática pa la enerxía cinético ye:

${\displaystyle Y_{c}=Y_{tra}+Y_{rot}={\frac {1}{2}}m\|\mathbf {v} \|^{2}+{\frac {1}{2}}{\boldsymbol {\omega }}^{t}\cdot (\mathbf {I} {\boldsymbol {\omega }})}$

Onde:

${\displaystyle Y_{tra}\;}$ Enerxía de traslación.

${\displaystyle Y_{rot}\;}$ Enerxía de rotación.

${\displaystyle m\,}$ Masa del cuerpu.

${\displaystyle \mathbf {I} }$ tensor de (momentos de) inercia.

${\displaystyle {\boldsymbol {\omega }}=}$ velocidá angular del cuerpu.

${\displaystyle {\boldsymbol {\omega }}^{t}=}$ trespuesta del vector de la velocidá angular del cuerpu.

${\displaystyle \mathbf {v} =}$ velocidá llinial del cuerpu.

El valor de la enerxía cinético ye positivu, y depende del sistema de referencia que se considere al determinar el valor (módulu) de la velocidá ${\displaystyle \mathbf {v} }$ y ${\displaystyle {\boldsymbol {\omega }}}$. La espresión anterior puede deducise de la espresión xeneral:

${\displaystyle Y_{c}=\int _{M}{\frac {\|\mathbf {v} \|^{2}}{2}}dm}$

Enerxía cinética en mecánica relativista

Enerxía cinética d'una partícula

Si la velocidá d'un cuerpu ye una fracción significante de la velocidá de la lluz, ye necesariu utilizar mecánica relativista pa poder calcular la enerxía cinético. En relatividá especial, tenemos de camudar la espresión pal momentu llinial y della por interacción puede deducise la espresión de la enerxía cinético:

${\displaystyle Y_{c}=m\gamma c^{2}-mc^{2}={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}}-mc^{2}}$

Tomando la espresión relativista anterior, desenvolviéndola en serie de Taylor y tomando namái'l términu ${\displaystyle (1/2)m(v^{2}/c^{2})}$ recupérase la espresión de la enerxía cinético típica de la mecánica newtoniana:^[2]

${\displaystyle Y_{c}={\frac {mc^{2}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}-mc^{2}=mc^{2}\left[{\frac {1}{2}}\left({\frac {v^{2}}{c^{2}}}\right)+{\frac {3}{8}}\left({\frac {v^{2}}{c^{2}}}\right)^{2}+...\right]={\frac {1}{2}}mv^{2}}$

Tómase namái'l primer términu de la serie de Taylor yá que, conforme la serie progresa, los términos vuélvense cada vez más y más pequeños y ye posible desprecialos.

La ecuación relativista amuesa que la enerxía d'un oxetu averar al infinitu cuando la velocidá v averar a la velocidá de la lluz c, entós ye imposible acelerar un oxetu a eses magnitúes. Esti productu matemáticu ye la fórmula d'equivalencia ente masa y enerxía, cuando'l cuerpu ta en reposu llogramos esta ecuación:

${\displaystyle Y_{0}=mc^{2}\!}$

Asina, la enerxía total Y puede particionarse ente les enerxíes de les mases en reposu más la tradicional enerxía cinético newtoniana de baxa velocidá. Cuando los oxetos mover a velocidaes muncho más baxes que la lluz (ej. cualquier fenómenu na tierra) los primeros dos términos de la serie predominen.

La rellación ente enerxía cinético y momentum ye más complicada nesti casu y vien dada pola ecuación:

${\displaystyle Y_{c}={\sqrt {p^{2}c^{2}+m^{2}c^{4}}}-mc^{2}}$

Esto tamién puede espandise como una serie de Taylor, el primer términu d'esta simple espresión vien de la mecánica newtoniana. Lo que suxer esto ye que les fórmules pa la enerxía y el momentu nun son especiales nin axomátiques pero dalgunos conceutos remanecen de les ecuaciones de masa con enerxía y de los principios de la relatividá.

Enerxía cinética d'un sólidu en rotación

A diferencia del casu clásicu la enerxía cinético de rotación en mecánica relativista nun puede ser representada a cencielles por un tensor d'inercia y una espresión cuadrática a partir d'él nel qu'intervenga la velocidá angular. El casu simple d'una esfera en rotación ilustra esti puntu; si suponemos una esfera d'un material abondo ríxido por que podamos despreciar les deformaciones por culpa de la rotación (y por tanto los cambeos de densidá) y tal que la so velocidá angular satisfaiga la condición ${\displaystyle \scriptstyle \omega R<c}$ puede calculase la enerxía cinético ${\displaystyle \scriptstyle Y_{c}}$ a partir de la siguiente integral:

${\displaystyle Y_{c}+m_{0}c^{2}=\int _{S}{\frac {c^{2}dm}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=2\pi \int _{r=0}^{r=R}\int _{\theta =0}^{\theta =\pi }{\frac {\rho c^{2}}{\sqrt {1-{\frac {r^{2}\omega ^{2}}{c^{2}}}}}}r^{2}\sin \theta drd\theta }$

Integrando la espresión anterior llógrase la espresión:

${\displaystyle Y_{c}={\frac {3}{2}}m_{0}c^{2}\left({\frac {c}{R\omega }}\right)^{2}\left[1+{\frac {1}{2}}\left({\frac {R\omega }{c}}-{\frac {c}{R\omega }}\right)\ln \left({\frac {c+R\omega }{c-R\omega }}\right)\right]-m_{0}c^{2}}$

Comparanza ente la espresión pa la enerxía cinético d'una esfera acordies cola mecánica clásica y la teoría de la relatividá mecánica relativista (equí R ye'l radiu, ω la velocidá angular y m₀ la masa en reposu de la esfera.

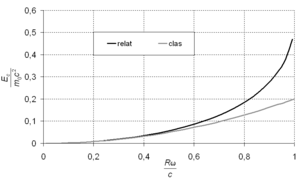
Pa una esfera en rotación los puntos sobre la exa nun tienen velocidá de traslación ente que los puntos más alloñaos de la exa de xiru tienen una velocidá ${\displaystyle \scriptstyle \omega R}$, a midida que esta velocidá averar a la velocidá de la lluz la enerxía cinético de la esfera tiende a crecer ensin llende. Esto oldea cola espresión clásica que se da de siguío:

${\displaystyle Y_{c}={\frac {1}{2}}I\omega ^{2}={\frac {1}{2}}\left({\frac {2}{5}}m_{0}R^{2}\right)\omega ^{2}}$

Paradóxicamente, dientro de la teoría especial de la relatividá, el supuestu de que ye posible construyir un sistema rotar progresivamente más rápidu una esfera sobre la so exa, lleva a que los puntos más alloñaos de la exa de xiru algamen la velocidá de la lluz aplicando al cuerpu una cantidá finita d'enerxía ${\displaystyle (Y_{c}=mR^{2}\omega ^{2}/2)}$. Lo cual revela que'l supuestu nun puede ser correutu cuando dellos puntos de la periferia del sólidu tán moviéndose a velocidaes cercanes a la de la lluz.

Enerxía cinética en mecánica cuántica

Na mecánica cuántica, el valor que s'espera d'enerxía cinético d'un electrón, ${\displaystyle \langle {\hat {T}}\rangle }$, pa un sistema d'electrones describe una función d'onda ${\displaystyle \vert \psi \rangle }$ que ye la suma d'un electrón, l'operador espérase qu'algame'l valor de:

${\displaystyle \langle {\hat {T}}\rangle =-{\frac {\hbar ^{2}}{2m_{y}}}{\bigg \langle }\psi {\bigg \vert }\sum _{i=1}^{N}\nabla _{i}^{2}{\bigg \vert }\psi {\bigg \rangle }}$

onde ${\displaystyle m_{y}}$ ye la masa d'un electrón y ${\displaystyle \nabla _{i}^{2}}$ ye'l operador laplaciano qu'actúa nes coordenaes del electrón i-ésimo y la suma de tolos otros electrones. Note que ye una versión cuantizada d'una espresión non relativista d'enerxía cinético en términos pel momento:

${\displaystyle Y_{c}={\frac {p^{2}}{2m}}}$

El formalismu de la teoría del funcional de la densidá funcional de densidá en mecánica cuántica rique una conocencia sobre la densidá electrónica, pa esto formalmente nun se riquir conocencies de la función d'onda.

Dau una densidá electrónica ${\displaystyle \rho (\mathbf {r} )}$, la funcional exacta de la enerxía cinético del n-ésimo electrón ye incierta; sicasí, nun casu específicu d'un sistema d'un electrón, la enerxía cinético puede escribise asina:

${\displaystyle T[\rho ]={\frac {1}{8}}\int {\frac {\nabla \rho (\mathbf {r} )\cdot \nabla \rho (\mathbf {r} )}{\rho (\mathbf {r} )}}d^{3}r}$

onde ${\displaystyle T[\rho ]}$ ye conocida como la funcional de la enerxía cinético de Von Weizsacker.

Enerxía cinética de partícules na mecánica cuántica

Na teoría cuántica una magnitú física como la enerxía cinético tien de venir representada por un operador autoadjunto nun espaciu de Hilbert fayadizu. Esi operador puede construyise por un procesu de cuantización, que conduz pa una partícula moviéndose pel espaciu euclidianu tridimensional a una representación natural d'esi operador sobre'l espaciu de Hilbert ${\displaystyle L^{2}(\mathbb {R} )}$ dau por:

${\displaystyle {\hat {Y}}_{c}=-\hbar ^{2}\left({\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}\right)}$

que, sobre un dominiu trupu de dichu espaciu formáu clases d'equivalencia representables por funciones C², define un operador autoadjunto con autovalores siempres positivos, lo cual fai que sían interpretables como valores físicamente medibles de la enerxía cinético.

Enerxía cinética del sólidu ríxidu na mecánica cuántica

Un sólidu ríxidu a pesar de tar formáu por un númberu infinitu de partícules, ye un sistema mecánicu con un númberu finito de graos de llibertá lo cual fai que'l so equivalente cuánticu pueda ser representáu por sobre un espaciu de Hilbert de dimensión infinita de tipu L² sobre un espaciu de configuración de dimensión finita. Nesti casu l'espaciu de configuración d'un sólidu ríxidu ye precisamente'l grupu de Lie SO(3) y per tantu l'espaciu de Hilbert pertinente y l'operador enerxía cinético de rotación pueden representase por:

${\displaystyle {\mathcal {H}}=L^{2}({\text{SO}}(3),\mu _{h})\qquad {\hat {Y}}_{rot}=\left({\frac {{\hat {L}}_{x}^{2}}{2I_{1}}}+{\frac {{\hat {L}}_{y}^{2}}{2I_{2}}}+{\frac {{\hat {L}}_{z}^{2}}{2I_{3}}}\right)}$

onde ${\displaystyle \mu _{h}}$ ye la midida de Haar invariante de SO(3), ${\displaystyle {\hat {L}}_{i}}$ son los operadores del momentu angular na representación fayadiza y esguilar ${\displaystyle I_{i}}$ son los momentos d'inercia principales.

Enerxía cinética y temperatura

Artículos principales: Teoría cinética y Baturiciu térmicu

A nivel microscópicu la enerxía cinético permediu de les molécules d'un gas define'l so temperatura. Acordies cola llei de Maxwell-Boltzmann pa un gas ideal clásicu la rellación ente la temperatura absoluto (T) d'un gas y la so enerxía cinético media ye:

${\displaystyle T={\frac {2}{3\kappa _{B}}}\langle Y_{k}\rangle ={\frac {m}{3\kappa _{B}}}\langle v^{2}\rangle }$

onde ${\displaystyle \kappa _{B}}$ ye la constante de Boltzmann, ${\displaystyle m\;}$ ye la masa de caúna de les molécules del gas.

Ver tamién

• Masa inercial
• Enerxía potencial
• Enerxía mecánica
• Movimientu browniano
• Teorema de la enerxía cinético
• Vis viva
• Enerxía eólica

Referencies

1. «Center of Mass Reference Frame». Archiváu dende l'orixinal, el 2007-06-11.
2. Resnick, R.; Halliday, D.; Krane, K. S. (2001). «Trabajo y energía», Física Vol. 1, 4ª edición n'inglés; n'español, 3ª, compañía Editorial Mexicana; John Wiley and Sons Inc, páx. 162. ISBN 968-26-1230-6.

Bibliografía

• Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed., Brooks/Cole. ISBN 0-534-40842-7.
• Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed., W. H. Freeman. ISBN 0-7167-0809-4.
• Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics, 4th ed., W. H. Freeman. ISBN 0-7167-4345-0.

Enllaces esternos