Seición cónica

Seición cónica
curva alxebraica, plane curve ^(en) , llugar xeométricu, seición y quadratic curve ^(en)

Los cuatro exemplos d'interseición d'un planu con un conu: parábola (1), elipse y circunferencia (2) ya hipérbola (3).

Conócense por seición cónica (o a cencielles cónica) a toles curves resultantes de les distintes interseiciones ente un conu y un planu; si dichu planu nun pasa pol vértiz, llógrense les cóniques puramente diches. Clasificar en cuatro tipos: elipse, parábola, hipérbola y circunferencia.

Etimoloxía

La primera definición conocida de seición cónica surde na Antigua Grecia, cerca del añu 340 a.C (Menecmo) onde les definieron como seiciones «d'un conu circular rectu».^[1] Los nomes d'hipérbola, parábola y elipse deber a Apolonio de Perge. Anguaño, les seiciones cóniques pueden definise de delles maneres; estes definiciones provienen de les diverses cañes de la matemática: como la xeometría analítica, la xeometría proyectiva, etc.

Tipos

Ficheru:Cono y seiciones.svg

Perspeutiva de les seiciones cóniques.

Los cuatro seiciones cóniques nel planu.

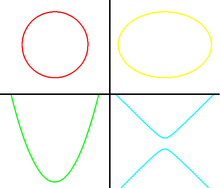
En función de la rellación esistente ente l'ángulu de conicidad (α) y l'enclín del planu respectu de la exa del conu (β), pueden llograse distintes seiciones cóniques, a saber:

• β < α : Hipérbola (naranxa)
• β = α : Parábola (azuláu)
• β > α : Elipse (verde)
• β = 90º: Circunferencia (un casu particular d'elipse) (colloráu)

Y β= 180° : Triangular

Si'l planu pasa pol vértiz del conu, puede comprobase que:

• Cuando β > α la interseición ye un únicu puntu (el vértiz).
• Cuando β = α la interseición ye una recta generatriz del conu (el planu va ser tanxente al conu).
• Cuando β < α la interseición va venir dada por dos rectes que se corten nel vértiz.
• Cuando β = 90º L'ángulu formáu poles rectes va dir aumentando a midida β mengua,cuando'l planu contenga a la exa del conu (β = 0).

Espresión alxebraica

Partiendo d'una circunferencia (y=0), al aumentar la escentricidá llógrense elipses, paráboles ya hipérboles.

En coordenaes cartesianes, les cóniques espresar en forma alxebraica por aciu ecuaciones cuadráticas de dos variables (x,y) de la forma:

${\displaystyle ax^{2}+2hxy+by^{2}+2gx+2fy+c=0\,}$

na que, en función de los valores de los parámetros, va tenese:

h² > ab: hipérbola.

h² = ab: parábola.

h² < ab: elipse.

a = b y h = 0: circunferencia.

a:C y Z:0: triangular

Por aciu un software pueden representase les gráfiques de la ecuación xeneral de les cóniques. De siguío preséntense los trés casos: Parábola, elipse ya hipérbola.

Esta gráfica representa una parábola xirada un determináu ángulu.

Esta gráfica representa una elipse xirada con un ciertu ángulu.

Esta gráfica representa una hipérbola xirada un determináu ángulu.

Carauterístiques

La elipse ye'l llugar xeométricu de los puntos del planu tales que la suma de les distancies a dos puntos fixos llamaos focos ye constante.

Amás de los focos F y F′, nuna elipse destáquense los siguientes elementos:

• Centru, O
• Exa mayor, AA′
• Exa menor, BB′
• Distancia focal, OF

La elipse con centru (0, 0) tien la siguiente espresión alxebraica: ${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$

La hipérbola ye'l llugar xeométricu de los puntos del planu que la so estrema de distancies a dos puntos fixos, llamaos focos, ye constante y menor que la distancia ente los focos.

Tien dos asíntotas (rectes que les sos distancies a la curva tienden a cero cuando la curva alloñar escontra l'infinitu). Les hipérboles que les sos asíntotas son perpendiculares llámense hipérboles equilláteres.

Amás de los focos y de les asíntotas, na hipérbola destáquense los siguientes elementos:

• Centru, O
• Vértices, A y A
• Distancia ente los vértices
• Alloña ente los focos

La ecuación d'una hipérbola horizontal con centru (0, 0), ye: ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$ De la mesma, la d'una hipérbola vertical ye: ${\displaystyle {\frac {y^{2}}{a^{2}}}-{\frac {x^{2}}{b^{2}}}=1}$

La parábola ye'l llugar xeométricu de los puntos del planu que equidistan d'un puntu fixu llamáu focu, y de una recta llamada directriz.

Amás del focu, F, y de la directriz, d'una parábola destáquense los siguientes elementos:

• Exa, y
• Vértiz, V
• Distancia de F a d, p.

Una parábola, que'l so vértiz ta nel orixe y la so exa coincide col d'ordenaes, tien la siguiente ecuación: ${\displaystyle \ y=a{x^{2}}\,}$

Aplicaciones

Les curves cóniques son importantes en astronomía: dos cuerpos masivos que interactúan según la llei de gravitación universal, les sos trayectories describen seiciones cóniques si'l so centru de masa considerar en reposu. Si tán relativamente próximes van describir elipses, si allóñense demasiáu van describir hipérboles o paráboles.

Tamién son importantes en aerodinámica y na so aplicación industrial, yá que dexen ser repitíes per medios mecánicos con gran exactitú, llogrando superficies, formes y curves perfectes.

Ver tamién

Seición cónica dexenerada

Curves cóniques

• Circunferencia
• Elipse
• Parábola
• Hipérbola
• Cuádrica
• Esferes de Dandelin

Aplicaciones

• Aerodinámica
• Astronomía
• Morfoloxía (diseñu)
• Gravitación
• Xeometría proyectiva

Notes y referencies

1. Oswald Veblen, John Wesley Young, Proyective Geometry, vol I, Ginn & Co. Ed. (1910)

Enllaces esternos

• Wikimedia Commons acueye conteníu multimedia sobre seiciones cóniques.
• Curves cóniques en laslaminas.es (14/5/12)
• Cóniques en wmatem.eis.uva.es (enllaz rotu disponible n'Internet Archive; ver l'historial y la última versión).