Parabola

Parabola, onun fokus məsafəsi və direktrisası
Kəsik konus:
Eksentrisitet:	${\displaystyle ~\textstyle e=1}$
Bərabərlik:	${\displaystyle ~\textstyle y^{2}=2px}$
Hiperbola  · Parabola  · Ellips  · Çevrə

Parabola (yun. παραβολή, tətbiq) — kvadratik funksiyanın (y = x²) qrafikinə verilən addır. Parabola Hiperbolanın tərsidir. Parabola dedikdə müstəvinin elə nöqtələrinin həndəsi yeri başa düşülür ki, bu nöqtələrin müstəvinin verilmiş düz xəttindən və verilmiş nöqtəsində olan məsafələri bir-birinə bərabər olsun. Müstəvinin verilmiş bu düz xəttinə parabolanın direktirisi, verilmiş nöqtəsinə isə parabolanın fokusu deyilir. Parabolanın fokusunu adətən ${\displaystyle F}$ ilə işarə edirlər.

Bərabərlik

Düzxətli koordinat sistemi üzərində Parabolanın kanonik şəkli aşağıdakı kimidir:

${\displaystyle ~\textstyle y^{2}=2px,p>0}$ (ya da ${\displaystyle ~\textstyle x^{2}=2py}$, əgər uc nöqtələrinin yernini dəyişdirsək).

Nəticə

Direktrisanın bərabərliyi: ${\displaystyle ~PQ}$: ${\displaystyle ~\textstyle x+{\frac {p}{2}}=0}$, fokus — ${\displaystyle ~\textstyle F\left({\frac {p}{2}};0\right)}$, buna əsasən koordinat başlanğıcı: ${\displaystyle ~O}$ — mərkəzin kəsiyi ${\displaystyle ~CF}$. Parabolanın ${\displaystyle ~M}$ üçün tapılmış müxtəlif nöqtəsində, üzərində yerləşən bərabərlik alınır: ${\displaystyle ~KM=FM}$. ${\displaystyle ~\textstyle KM=KD+DM={\frac {p}{2}}+x}$ və ${\displaystyle ~\textstyle FM={\sqrt {\left(x-{\frac {p}{2}}\right)^{2}+y^{2}}}}$, onda bərabərlik aşğıdakı görünüşünü alır: ${\displaystyle ~{\sqrt {\left(x-{\frac {p}{2}}\right)^{2}+y^{2}}}={\frac {p}{2}}+x}$. Bərabərliyi müxtəlif cür hesabladıqdan sonra eynigüclü bərabərlik alınır: ${\displaystyle ~y^{2}=2px}$.

Kvadrat tənlik: ${\displaystyle ~y=ax^{2}+bx+c}$ при ${\displaystyle ~a\neq 0}$ həmçinin, parabolanın и qrafikini əks etdirir, bu düstur kimi: ${\displaystyle ~y=ax^{2}}$, ancaq birinci bərabərlik ikinci bərabərlikdən ona görə fərqlənir ki, birinci bərabərliyin başlanğıcı koordinat başlanğıcı üzərində deyildir. ${\displaystyle ~A}$-nın müxtəlif nöqtələri üçün koordinat aşağıdakı düsturla hesablanır:

${\displaystyle ~x_{A}=-{\frac {b}{2a}},\;y_{A}=-{\frac {D}{4a}},}$ haradakı: ${\displaystyle D=b^{2}-4ac}$ — Diskriminant. Həmçinin: ${\displaystyle ~y=ax^{2}+bx+c}$ kvadratik tənliyi ${\displaystyle ~y=a(x-x_{A})^{2}+y_{A}}$ bu şəkildə də göstərilə bilər. Əgər ${\displaystyle ~A}$ nöqtəsi koordinat siteminin başlanğıcı üzərində olarsa kanonik şəkildə göstərilə bilər. Bu zaman: ${\displaystyle p={\frac {1}{|2a|}}}$ ifadəsi meydana çıxır.

Kvadrat tənliyinin əmsallarının hesablanması

Əgər ${\displaystyle ~y=ax^{2}+bx+c}$ tənliyi üçün tapılmış üç nöqtə üçün ${\displaystyle ~(x_{1};y_{1})}$, ${\displaystyle ~(x_{2};y_{2})}$, ${\displaystyle ~(x_{3};y_{3})}$ ifadələr alınarsa, onda kvadrat tənliyinin əmsallarını aşağıdakı kimi hesablamaq olar:

${\displaystyle ~a={\frac {y_{3}-{\frac {x_{3}(y_{2}-y_{1})+x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}}{x_{3}(x_{3}-x_{1}-x_{2})+x_{1}x_{2}}},b={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}-a(x_{1}+x_{2}),c={\frac {x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}+ax_{1}x_{2}}$

Digər bərabərliklər

Şaquli simmetriyanın ucları

${\displaystyle (x-h)^{2}=4p(y-k)\,}$

${\displaystyle y={\frac {(x-h)^{2}}{4p}}+k\,}$

${\displaystyle y=ax^{2}+bx+c\,}$

haradakı:

${\displaystyle a={\frac {1}{4p}};\ \ b={\frac {-h}{2p}};\ \ c={\frac {h^{2}}{4p}}+k;\ \ }$

${\displaystyle h={\frac {-b}{2a}};\ \ k={\frac {4ac-b^{2}}{4a}}}$. Parametrik forması:

${\displaystyle x(t)=2pt+h;\ \ y(t)=pt^{2}+k\,}$

Üfüqi simmetriyanın ucları

${\displaystyle (y-k)^{2}=4p(x-h)\,}$

${\displaystyle x={\frac {(y-k)^{2}}{4p}}+h;\ \,}$

${\displaystyle x=ay^{2}+by+c\,}$

haradakı:

${\displaystyle a={\frac {1}{4p}};\ \ b={\frac {-k}{2p}};\ \ c={\frac {k^{2}}{4p}}+h;\ \ }$

${\displaystyle h={\frac {4ac-b^{2}}{4a}};\ \ k={\frac {-b}{2a}}}$. Parametrik forması:

${\displaystyle x(t)=pt^{2}+h;\ \ y(t)=2pt+k\,}$

Baş parabola

Parabola üçün ümumi düstur aşağıdakı kimidir:

${\displaystyle (\alpha x+\beta y)^{2}+\gamma x+\delta y+\epsilon =0\,}$

${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\,}$

və aşağıdakı kimi ifadə üçün doğrudur,

${\displaystyle B^{2}=4AC\,}$.

Baş parabola üçün fokus tənliyi: F(u, v), və a direktriks üçün düstur:

${\displaystyle ax+by+c=0\,}$

is

${\displaystyle {\frac {\left(ax+by+c\right)^{2}}{{a}^{2}+{b}^{2}}}=\left(x-u\right)^{2}+\left(y-v\right)^{2}\,}$

Qauss xəritəsinin forması

Qauss xəritəsinin forması aşağıdakı kimidir: ${\displaystyle (\tan ^{2}\phi ,2\tan \phi )}$ tənliyin ifadəsi aşağıdakı ifadə kimi eynigüclüdür: ${\displaystyle (\cos \phi ,\sin \phi )}$.

Polyar koordinatda parabola

Polyar koordinatda olan parabola üçün aşağıdakı bərabərliklər vardır:

${\displaystyle r(\varphi )=4a{\frac {\cos(\varphi )}{\sin ^{2}(\varphi )}}\quad \ \varphi \in \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]\setminus \{0\}.}$

${\displaystyle (a,0)}$.

${\displaystyle r(\varphi )={\frac {2a}{1-\cos(\varphi )}}\quad \ \varphi \neq 2\pi k.}$

Fəzada Parabola

Bir sıra kosmik cisimlərin trayektoriyası (kometlər, asteroidlər və s.) böyük sürətlə parabolaya oxşayırlar. Parabola konus ailəsinin bir hissəsinə aiddir. Parabolanın formasından bir sıra arxitekturada istifadə edilir.

• 
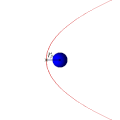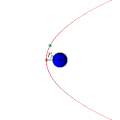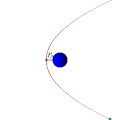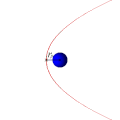
  Parabolik orbit
• 
  Basketbol topunun düşməsi
• 
• 
• 
• 
  Parabolanın konus şəkli

Həmçinin bax

• Hiperbola

Xarici keçidlər

• Animierte Parabel
• Apollonius' Derivation of the Parabola*
• Interactive parabola-drag focus, see axis of symmetry, directrix, standard and vertex forms
• Archimedes Triangle and Squaring of Parabola
• Two Tangents to Parabola
• Parabola As Envelope of Straight Lines
• Parabolic Mirror
• Three Parabola Tangents
• Module for the Tangent Parabola
• Focal Properties of Parabola
• Parabola As Envelope II
• The similarity of parabola
• Dynamic Geometry Sketches, interactive dynamic geometry sketch.
• a method of drawing a parabola with string and tacks Arxivləşdirilib 2010-09-01 at the Wayback Machine