Бишмөйөш

Бишмөйөш
Алдағы	дүртмөйөш
Тәртип буйынса һуңыраҡ килеүсе	алтымөйөш
Имеет вершинную фигуру	киҫек^[d]
Грань политопа	ҡабырға^[d]
Вики-проект	Проект:Математика^[d]
Бишмөйөш Викимилектә

Бишмөйөш — биш мөйөшө булған күпмөйөш. Шулай уҡ шундай формалағы һәр нәмәне бишмөйөш тип атайҙар.

Эргәләш булмаған яҡтары киҫешмәгән бишмөйөштөң майҙаны

Түбәләренең координаталары менән бирелгән, эргәләш булмаған яҡтары киҫешмәгән бишмөйөштөң майҙаны, күпмөйөштәр өсөн дөйөм булған формула буйынса иҫәпләнә.

Ҡабарынҡы бишмөйөш

Ҡабарынҡы бишмөйөш тип, бөтә нөктәләре лә уның ике күрше түбәһе аша үтеүсе теләһә ниндәй тура һыҙыҡтан бер яҡта ятҡан бишмөйөш атала.

Ҡабарынҡы бишмөйөштөң эске мөйөштәренең суммаһы 540°-ҡа тигеҙ.

${\displaystyle \sum _{i=1}^{5}\alpha _{i}=(5-2)\cdot 180^{\circ }=3\cdot 180^{\circ }=540^{\circ }}$

Төҙөк бишмөйөш (пентагон)

Төҙөк бишмөйөш

Төп мәҡәлә: Төҙөк бишмөйөш

Пентагон йәки төҙөк бишмөйөш тип, бөтә яҡтары һәм бөтә мөйөштәре тигеҙ булған бишмөйөш атала.

Әгәр пентагонда диагоналдәрен үткәрһәң, ул^[1]:

• бәләкәйерәк пентагонға (диагоналдәренең киҫешеү нөктәләре менән яһала) — үҙәктә
• бәләкәйерәк пентагон эргәһендә — ике төрҙәге биш тигеҙ эргәле өсмөйөшкә (эргә яғының нигеҙенә сағыштырмаһы алтын пропорцияға тигеҙ булған):
  • 1) тубәһендәге ҡыҫынҡы мөйөштәре 36° һәм нигеҙе эргәһендәге ҡыҫынҡы мөйөштәре 72°
  • 2) түбәһендәге йәйенке мөйөшө 108° һәм нигеҙе эргәһендәге ҡыҫынҡы мөйөштәре 36°

бүленә.

Беренсе ике һәм икенсе ике өсмөйөштәрҙе уларҙың нигеҙҙәре менән тоташтырғанда, ике «алтын» ромб (беренсеһенең ҡыҫынҡы мөйөшө 36° һәм йәйенке мөйөшө 144°) барлыҡҡа килә. Роджер Пенроуз «алтын» ромбтарҙы «алтын» паркет (Пенроуз мозаикаһы) төҙөү өсөн ҡулланған.

Йондоҙ һымаҡ бишмөйөштәр

Төп мәҡәлә: Пентаграмма

Пентаграмманың алтын киҫелештәре

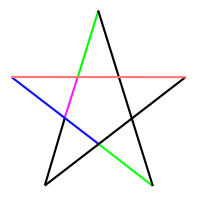
Бөтә яҡтары һәм бөтә мөйөштәре тигеҙ булған, ә түбәләре төҙөк күпмөйөштөң түбәләре менән тап килгән күпмөйөш йондоҙ һымаҡ күпмөйөш тип атала. Төҙөк бишмөйөштән башҡа тағы ла бер йондоҙ һымаҡ бишмөйөш бар — пентаграмма.

Пентаграмма, Пифагор уйлағанса, математик камиллыҡ булып тора, сөнки алтын киҫелеште (φ = (1+√5)/2 = 1,618…) күрһәтә. Әгәр теләһә ҡайһы төҫлө киҫектең оҙонлоғон ҡалған ҡыҫҡараҡ киҫектәрҙең иң оҙононоң оҙонлоғона бүлһәң, алтын киҫелеш φ килеп сыға.

${\displaystyle \varphi ={\frac {\mathrm {\color {red}red} }{\mathrm {\color {Blue}blue} }}={\frac {\mathrm {\color {Blue}blue} }{\mathrm {\color {Green}green} }}={\frac {\mathrm {\color {Green}green} }{\mathrm {\color {Magenta}magenta} }}}$

Шулай уҡ ҡарағыҙ

• Төҙөк бишмөйөш
• Пентагон
• Пентаграмма

Иҫкәрмәләр

1. Плитки Пенроуза

<onlyinclude>

<onlyinclude>