Радыян
| Радыян | |
|---|---|
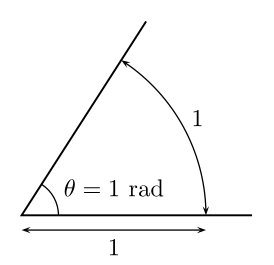 | |
 | |
| Абазначэнне адзінкі | rad[1][2][…], рад, rad, рад, rad, rad, rad і rad |
| Формула, якая апісвае закон або тэарэму | |
| Пазначэнне ў формуле | |
| Пераўтварэнні да асноўнай адзінкі СІ | 1 радыян |
| Фізічная велічыня | angular measure[d][2][3] |
| Subdivision of this unit | deciradian[d] |

Радыя́н[4] (беларускае абазначэнне: рад, міжнароднае: rad;[5] лац.: radius — прамень, радыус) — асноўная адзінка вымярэння плоскіх вуглоў у сучаснай матэматыцы і фізіцы. Радыян вызначаецца як вуглавая велічыня дугі, даўжыня якой роўная яе радыусу. Такім чынам, велічыня поўнага вугла роўная 2π радыян.
Даўжыня дугі акружнасці радыуса R і вуглавой велічыні α, вымеранай ў радыянах, роўная Rα.
Велічыня вугла, выражаная ў радыянах, роўная дзелі даўжыні дугі акружнасці на даўжыню яе радыуса, таму радыян — велічыня безразмерная. Па той жа прычыне абазначэнне радыяна (рад) часта апускаецца.
Сувязь радыяна з іншымі адзінкамі
[правіць | правіць зыходнік]
Суадносіны радыяна з іншымі адзінкамі вымярэння вуглоў апісваюцца формулай:
1 радыян = (1/(2π)) абароту = 180 / π градусаў = 200 / π градаў.
Відавочна, 180° = π радыян. Адсюль выцякае простая формула пераводу з градусаў, хвілін і секунд у радыяны і наадварот.
α [рад] = α [°] × (π / 180);
α [°] = α [рад] × (180 / π),
дзе α [рад] — вугал у радыянах, α [°] — вугал у градусах
1 рад ≈ 57,295779513° ≈ 57°17’44, 806" ≈ 206265".
Радыянная мера ў матэматычным аналізе
[правіць | правіць зыходнік]Пры разглядзе трыганаметрычных функцый у матэматычным аналізе, як правіла, лічаць, што аргумент вымяраецца ў радыянах, гэта спрашчае формулы і запісы разлікаў.
Пры малых вуглах сінус і тангенс вугла, выражанага ў радыянах, прыблізна роўныя самому вуглу, што зручна пры набліжаных вылічэннях:
Гл. таксама
[правіць | правіць зыходнік]Зноскі
- ↑ Logopedia
- ↑ а б 6.5.3 // Quantities and units—Part 1: General — 1 — ISO, 2009. — P. 18. — 41 p.
- ↑ SI A concise summary of the International System of Units, SI — 2019.
- ↑ БелЭн 2001.
- ↑ ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин. Архівавана 10 лістапада 2012.
Літаратура
[правіць | правіць зыходнік]- Радыян // Беларуская энцыклапедыя: У 18 т. Т. 13: Праміле — Рэлаксін / Рэдкал.: Г. П. Пашкоў і інш. — Мн. : БелЭн, 2001. — Т. 13. — С. 240. — 10 000 экз. — ISBN 985-11-0035-8. — ISBN 985-11-0216-4 (т. 13).
Спасылкі
[правіць | правіць зыходнік]- «Углы, градусы и радианы» — пераклад артыкула Intuitive Guide to Angles, Degrees and Radians | BetterExplained (англ.)



