Куб (алгебра)

У паняцця ёсць і іншыя значэнні, гл. Куб (значэнні).

y=x³, пры цэлых значэннях x на адрэзку ад 1 да 25

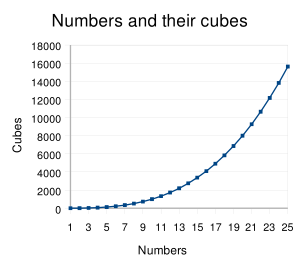
У арыфметыцы і алгебры, куб ліку x — гэта яго трэцяя ступень x³, г.зн. здабытак трох аднолькавых множнікаў, роўных ліку x:

x³ = x × x × x.

Куб ліку роўны здабытку самога ліку і яго квадрата:

x³ = x × x².

Аперацыя ўзвядзення ў куб мае просты геаметрычны сэнс: куб ліку x роўны аб'ёму геаметрычнага куба з рабром x, адкуль і паходзіць назва самой арыфметычнай аперацыі. Адваротная аперацыя знаходжання ліку, чый куб роўны n, называецца здабываннем кубічнага кораня з n і вызначае рабро куба з аб'ёмам n.

І куб, і кубічны корань з'яўляюцца няцотнымі функцыямі:

(−n)³ = −(n³).

Куб ліку ці любога іншага матэматычнага выразу абазначаецца верхнім індэксам 3, напрыклад, 2³ = 8 ці (x + 1)³.

Гісторыя

Вызначэнне кубоў вялікіх лікаў было распаўсюджана ў многіх старажытных цывілізацыях. У старававілонскі перыяд (20 — 16 стст. да н.э.) месапатамскія матэматыкі стварылі клінапісныя таблічкі з табліцамі для вылічэння кубоў і кубічных каранёў^[1][2]. Кубічныя ўраўненні былі вядомы старажытнагрэчаскаму матэматыку Дыяфанту^[3]. У 1-м ст. н.э. Герон Александрыйскі вынайшаў метад вылічэння кубічных каранёў^[4]. Метады рашэння кубічных ураўненняў і здабывання кубічных каранёў сустракаюцца ў «Матэматыцы ў дзевяці кнігах», кітайскім матэматычным тэксце, састаўленым каля 2-га ст. да н.э., з каментарыямі Лю Хуэя (3 ст. н.э.)^[5]. Індыйскі матэматык Арыябхата напісаў тлумачэнне кубоў у сваёй працы Арыябхація. У 2010 годзе Альберта Цаноні знайшоў новы алгарытм^[6] вылічэння кубоў вялікіх цэлых лікаў, які ў пэўным дыяпазоне значэнняў скарэйшы чым узвядзенне ў квадрат і дамнажэнне.

Паслядоўнасць кубоў

Паслядоўнасць кубоў неадмоўных лікаў пачынаецца лікамі^[7]:

1³ = 1	11³ = 1331	21³ = 9261	31³ = 29 791	41³ = 68 921	51³ = 132 651
2³ = 8	12³ = 1728	22³ = 10 648	32³ = 32 768	42³ = 74 088	52³ = 140 608
3³ = 27	13³ = 2197	23³ = 12 167	33³ = 35 937	43³ = 79,507	53³ = 148,877
4³ = 64	14³ = 2744	24³ = 13 824	34³ = 39 304	44³ = 85 184	54³ = 157 464
5³ = 125	15³ = 3375	25³ = 15 625	35³ = 42 875	45³ = 91 125	55³ = 166 375
6³ = 216	16³ = 4096	26³ = 17 576	36³ = 46 656	46³ = 97 336	56³ = 175 616
7³ = 343	17³ = 4913	27³ = 19 683	37³ = 50 653	47³ = 103 823	57³ = 185 193
8³ = 512	18³ = 5832	28³ = 21 952	38³ = 54 872	48³ = 110 592	58³ = 195 112
9³ = 729	19³ = 6859	29³ = 24 389	39³ = 59 319	49³ = 117 649	59³ = 205 379
10³ = 1000	20³ = 8000	30³ = 27 000	40³ = 64 000	50³ = 125 000	60³ = 216 000

Сума кубоў паслядоўных цэлых лікаў

Сума кубоў першых ${\displaystyle n}$ дадатных натуральных лікаў вылічаецца па формуле:

${\displaystyle \sum _{i=1}^{n}i^{3}=1^{3}+2^{3}+3^{3}+...+n^{3}=\left({\frac {n(n+1)}{2}}\right)^{2}.}$

Вывад формулы

Наглядны доказ таго, што 1³ + 2³ + 3³ + 4³ + 5³ = (1 + 2 + 3 + 4 + 5)²

Формулу сумы кубоў можна вывесці з дапамогай табліцы множання і формулы сумы арыфметычнай прагрэсіі^[8]. Разглядаючы ў якасці ілюстрацыі метаду дзве табліцы множання 5×5, правядзём разважанні для табліц памерам n×n.

Табліца множання і кубы лікаў × 1 2 3 4 5 1 1 2 3 4 5 2 2 4 6 8 10 3 3 6 9 12 15 4 4 8 12 16 20 5 5 10 15 20 25

Табліца множання і арыфметычная прагрэсія × 1 2 3 4 5 1 1 2 3 4 5 2 2 4 6 8 10 3 3 6 9 12 15 4 4 8 12 16 20 5 5 10 15 20 25

Сума лікаў у k-ай (k = 1,2, …) выдзеленай вобласці першай табліцы:

${\displaystyle k^{2}+2k\sum _{l=1}^{k-1}l=k^{2}+2k{\frac {k(k-1)}{2}}=k^{3}.}$

А сума лікаў у k-ай (k = 1,2, …) выдзеленай вобласці другой табліцы, якія ўяўляюць сабой арыфметычную прагрэсію:

${\displaystyle k\sum _{l=1}^{n}l=k{\frac {n(n+1)}{2}}.}$

Складваючы па ўсіх выдзеленых абласцях першай табліцы, атрымліваем такі ж лік, як і складваючы па ўсіх выдзеленых абласцях другой табліцы:

${\displaystyle \sum _{k=1}^{n}k^{3}=\sum _{k=1}^{n}k{\frac {n(n+1)}{2}}={\frac {n(n+1)}{2}}\sum _{k=1}^{n}k=\left({\frac {n(n+1)}{2}}\right)^{2}.}$

Геаметрычны сэнс

Куб ліку роўны аб'ёму куба з даўжынёй рабра, роўнай гэтаму ліку.

Дзесятковае разлажэнне

• У дзесятковым запісе куб можа заканчвацца на любую лічбу (у адрозненне ад квадрата)
• У дзесятковым запісе дзве апошнія лічбы куба могуць быць 00, 01, 03, 04, 07, 08, 09, 11, 12, 13, 16, 17, 19, 21, 23, 24, 25, 27, 28, 29, 31, 32, 33, 36, 37, 39, 41, 43, 44, 47, 48, 49, 51, 52, 53, 56, 57, 59, 61, 63, 64, 67, 68, 69, 71, 72, 73, 75, 76, 77, 79, 81, 83, 84, 87, 88, 89, 91, 92, 93, 96, 97, 99. Залежнасць перадапошняй лічбы куба ад апошняй можна прадставіць у выглядзе наступнай табліцы:

апошняя лічба	перадапошняя лічба
0	0
5	2, 7
4, 8	цотная
2, 6	няцотная
1, 3, 7, 9	любая

Гл. таксама

• Кубічны корань — адваротная аперацыя адносна ўзвядзення ў куб.
• Квадрат (алгебра)
• Чацвёртая ступень
• Пятая ступень
• Шостая ступень
• Сёмая ступень
• Восьмая ступень

Зноскі

1. Cooke, Roger (8 November 2012). The History of Mathematics. John Wiley & Sons. p. 63. ISBN 978-1-118-46029-0.
2. Nemet-Nejat, Karen Rhea (1998). Daily Life in Ancient Mesopotamia. Greenwood Publishing Group. p. 306. ISBN 978-0-313-29497-6.
3. Van der Waerden, Geometry and Algebra of Ancient Civilizations, chapter 4, Zurich 1983 ISBN 0-387-12159-5
4. Smyly, J. Gilbart (1920). "Heron's Formula for Cube Root". Hermathena. 19 (42). Trinity College Dublin: 64–67.
5. Crossley, John; W.-C. Lun, Anthony (1999). The Nine Chapters on the Mathematical Art: Companion and Commentary. Oxford University Press. pp. 176, 213. ISBN 978-0-19-853936-0.
6. http://www.springerlink.com/content/q1k57pr4853g1513/(недаступная спасылка)
7. паслядоўнасць A000578 у OEIS
8. Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Матезис, 1923. — С. 68—70.

Спасылкі

• Weisstein, Eric W.. Cubic Number (нявызн.). MathWorld.