Множанне матрыц

Мно́жанне ма́трыц — адна з асноўных аперацый над матрыцамі. Матрыца, атрыманая ў выніку аперацыі множання, называецца здабы́ткам ма́трыц. Элементы новай матрыцы атрымліваюцца з элементаў старых матрыц у адпаведнасці з правіламі, праілюстраванымі ніжэй.

Матрыцы ${\displaystyle A}$ і ${\displaystyle B}$ могуць быць памножаны, калі яны сумяшчальныя ў тым сэнсе, што колькасць слупкоў матрыцы ${\displaystyle A}$ роўная колькасці радкоў ${\displaystyle B}$.

Матрыцы маюць шматлікія алгебраічныя ўласцівасці множання, уласцівыя звычайным лікам, за выключэннем камутатыўнасці.

Для квадратных матрыц, акрамя множання, можа быць уведзена аперацыя ўзвядзення матрыцы ў ступень і адваротная матрыца.

Паколькі матрыцы выкарыстоўваюцца для апісання, у прыватнасці, пераўтварэнняў матэматычных прастораў (паварот, адлюстраванне, расцяжэнне і іншыя), здабытак матрыц будзе апісваць кампазіцыю пераўтварэнняў.

Азначэнне

Няхай дадзены дзве прамавугольныя матрыцы ${\displaystyle A}$ і ${\displaystyle B}$ памеру ${\displaystyle l\times m}$ і ${\displaystyle m\times n}$ адпаведна:

${\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1m}\\a_{21}&a_{22}&\cdots &a_{2m}\\\vdots &\vdots &\ddots &\vdots \\a_{l1}&a_{l2}&\cdots &a_{lm}\end{bmatrix}},\;\;\;B={\begin{bmatrix}b_{11}&b_{12}&\cdots &b_{1n}\\b_{21}&b_{22}&\cdots &b_{2n}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mn}\end{bmatrix}}.}$

Тады матрыца ${\displaystyle C}$ памеру ${\displaystyle l\times n}$:

${\displaystyle C={\begin{bmatrix}c_{11}&c_{12}&\cdots &c_{1n}\\c_{21}&c_{22}&\cdots &c_{2n}\\\vdots &\vdots &\ddots &\vdots \\c_{l1}&c_{l2}&\cdots &c_{ln}\end{bmatrix}},}$

у якой:

${\displaystyle c_{ij}=\sum _{r=1}^{m}a_{ir}b_{rj}\;\;\;\left(i=1,2,\ldots l;\;j=1,2,\ldots n\right).}$

называецца іх здабыткам.

Аперацыя множання двух матрыц магчымая толькі ў тым выпадку, калі колькасць слупкоў у першым множніку роўная колькасці радкоў у другім; у гэтым выпадку кажуць, што матрыцы ўзгодненыя. У прыватнасці, множанне заўсёды магчыма, калі абодва множнікі — квадратныя матрыцы аднаго і таго ж парадку.

Такім чынам, з існавання здабытку ${\displaystyle AB}$ зусім не вынікае існаванне здабытку ${\displaystyle BA}$.

Ілюстрацыя

Здабытак матрыц AB складаецца з усіх магчымых камбінацый скалярных здабыткаў вектар-радкоў матрыцы A і вектар-слупкоў матрыцы B. Элемент матрыцы AB з індэксамі i, j ёсць скалярным здабыткам i-га вектар-радка матрыцы A і j-га вектар-слупка матрыцы B.

Ілюстрацыя справа дэманструе вылічэнне здабытку дзвюх матрыц A і B, яна паказвае, як кожнае перасячэнне ў здабытку матрыц адпавядае радкам матрыцы A і слупкам матрыцы B. Памер выніковай матрыцы заўсёды максімальна магчымы, гэта значыць для кожнага радка матрыцы A і слупка матрыцы B заўсёды ёсць адпаведнае перасячэнне ў здабытку матрыцы.

Значэнні на перасячэннях, пазначаных кружочкамі, будуць:

${\displaystyle {\begin{aligned}{\color {Red}x_{1,2}}&=(a_{1,1},a_{1,2})\cdot (b_{1,2},b_{2,2})\\&=a_{1,1}b_{1,2}+a_{1,2}b_{2,2}\\{\color {Blue}x_{3,3}}&=(a_{3,1},a_{3,2})\cdot (b_{1,3},b_{2,3})\\&=a_{3,1}b_{1,3}+a_{3,2}b_{2,3}\end{aligned}}}$

У агульным выпадку, здабытак матрыц не з’яўляецца камутатыўнай аперацыяй. Напрыклад:

${\displaystyle {\overset {3\times 4{\text{ matrix}}}{\begin{bmatrix}\cdot &\cdot &\cdot &\cdot \\\cdot &\cdot &\cdot &\cdot \\\color {Blue}1&\color {Blue}2&\color {Blue}3&\color {Blue}4\\\end{bmatrix}}}{\overset {4\times 5{\text{ matrix}}}{\begin{bmatrix}\cdot &\cdot &\cdot &\color {Red}a&\cdot \\\cdot &\cdot &\cdot &\color {Red}b&\cdot \\\cdot &\cdot &\cdot &\color {Red}c&\cdot \\\cdot &\cdot &\cdot &\color {Red}d&\cdot \\\end{bmatrix}}}={\overset {3\times 5{\text{ matrix}}}{\begin{bmatrix}\cdot &\cdot &\cdot &\cdot &\cdot \\\cdot &\cdot &\cdot &\cdot &\cdot \\\cdot &\cdot &\cdot &x_{3,4}&\cdot \\\end{bmatrix}}}}$

Элемент ${\displaystyle x_{3,4}}$ здабытку матрыц, прыведзеных вышэй, вылічваецца наступным чынам

${\displaystyle x_{3,4}=({\color {Blue}1},{\color {Blue}2},{\color {Blue}3},{\color {Blue}4})\cdot ({\color {Red}a},{\color {Red}b},{\color {Red}c},{\color {Red}d})={\color {Blue}1}\cdot {\color {Red}a}+{\color {Blue}2}\cdot {\color {Red}b}+{\color {Blue}3}\cdot {\color {Red}c}+{\color {Blue}4}\cdot {\color {Red}d}}$

Першая каардыната ў абазначэнні матрыцы абазначае радок, другая каардыната — слупок; гэты парадак выкарыстоўваецца як пры індэксацыі, так і пры абазначэнні памеру. Элемент ${\displaystyle x_{{\color {Blue}i}{\color {Red}j}}}$ на перасячэнні радка ${\displaystyle i}$ і слупка ${\displaystyle j}$ выніковай матрыцы з’яўляецца скалярным здабыткам ${\displaystyle i}$-га радка першай матрыцы і ${\displaystyle j}$-га слупка другой матрыцы. Гэта тлумачыць чаму шырыня і вышыня множаных матрыц павінны супадаць: у адваротным выпадку скалярны здабытак не вызначаны.

Абмеркаванне

Убачыць прычыны апісанага правіла матрычнага множання прасцей за ўсё, разгледзеўшы множанне вектара на матрыцу.

Апошняе натуральна ўводзіцца зыходзячы з таго, што пры раскладзе вектараў па базісе дзеяння (любога) лінейнага аператара A дае выражэнне кампанентаў вектара v' = Av:

${\displaystyle v'_{i}=\sum \limits _{j}A_{ij}v_{j}}$

То бок лінейны аператар аказваецца прадстаўлены матрыцай, вектары — вектарамі-слупкамі, а дзеянне аператара на вектар — матрычным множаннем вектара-слупка злева на матрыцу аператара (гэта прыватны выпадак матрычнага множання, калі адна з матрыц — вектар-слупок — мае памер ${\displaystyle n\times 1}$).

(Пераход да любога новага базіса пры змене каардынат прадстаўляецца цалкам аналагічным выразам, толькі ${\displaystyle v'_{i}}$ у гэтым выпадку ўжо не кампаненты новага вектара ў старым базісе, а кампаненты старога вектара ў новым базісе; пры гэтым ${\displaystyle A_{ij}}$ — элементы матрыцы пераходу да новага базіса).

Разгледзеўшы паслядоўнае дзеянне на вектар двух аператараў: спачатку A, а потым B (або пераўтварэнне базіса A, а затым пераўтварэнне базіса B), двойчы прымяніўшы нашу формулу, атрымаем:

${\displaystyle v''_{i}=\sum \limits _{j}B_{ij}\sum \limits _{k}A_{jk}v_{k}=\sum \limits _{j}\sum \limits _{k}B_{ij}A_{jk}v_{k}=\sum \limits _{k}\sum \limits _{j}(B_{ij}A_{jk})v_{k},}$

адкуль відаць, што кампазіцыі BA дзеяння лінейных аператараў A і B (або аналагічнай кампазіцыі пераўтварэнняў базіса) адпавядае матрыца, вылічаная па правілу здабытку адпаведных матрыц:

${\displaystyle (BA)_{ik}=\sum \limits _{j}B_{ij}A_{jk}.}$

Вызначаны такім чынам здабытак матрыц аказваецца цалкам натуральным і відавочна карысным (дае просты і універсальны спосаб вылічэння кампазіцый адвольнай колькасці лінейных пераўтварэнняў).

Уласцівасці

Злучальная ўласцівасць, асацыятыўнасць:

${\displaystyle \mathbf {A} (\mathbf {BC} )=(\mathbf {AB} )\mathbf {C} ;}$

${\displaystyle \alpha (\mathbf {AB} )=(\alpha \mathbf {A} )\mathbf {B} =\mathbf {A} (\alpha \mathbf {B} ).}$

Размеркавальная ўласцівасць, дыстрыбутыўнасць адносна складання:

${\displaystyle \mathbf {A} (\mathbf {B} +\mathbf {C} )=\mathbf {AB} +\mathbf {AC} ;}$

${\displaystyle (\mathbf {A} +\mathbf {B} )\mathbf {C} =\mathbf {AC} +\mathbf {BC} .}$.

Здабытак матрыцы на адзінкавую матрыцу ${\displaystyle \mathbf {E} }$ адпаведнага парадку роўны самой матрыцы:

${\displaystyle \mathbf {EA} =\mathbf {A} ;}$

${\displaystyle \mathbf {AE} =\mathbf {A} .}$

Здабытак матрыцы на нулявую матрыцу ${\displaystyle \mathbf {0} }$ адпаведнага памеру роўны нулявой матрыцы:

${\displaystyle \mathbf {0A} =\mathbf {0} ;}$

${\displaystyle \mathbf {A0} =\mathbf {0} .}$

Калі ${\displaystyle \mathbf {A} }$ і ${\displaystyle \mathbf {B} }$ — квадратныя матрыцы аднаго і таго ж парадку, то здабытак матрыц валодае яшчэ шэрагам уласцівасцей.

Множанне матрыц у агульным выпадку некамутатыўна:

${\displaystyle \mathbf {AB} \neq \mathbf {BA} .}$

Калі ${\displaystyle \mathbf {AB} =\mathbf {BA} }$, то матрыцы ${\displaystyle \mathbf {A} }$ і ${\displaystyle \mathbf {B} }$ называюцца камутавальнымі паміж сабой.

Прасцейшыя прыклады камутавальных матрыц:

• любая квадратная матрыца — з самой сабой: ${\displaystyle \mathbf {AA} =\mathbf {AA} =\mathbf {A^{2}} }$ (узвядзенне матрыцы ў квадрат);
• любая квадратная матрыца — з адзінкавай матрыцай таго ж парадку: ${\displaystyle \mathbf {AE} =\mathbf {EA} =\mathbf {A} }$;
• любая квадратная матрыца — з нулявой матрыцай таго ж парадку: ${\displaystyle \mathbf {A0} =\mathbf {0A} =\mathbf {0} }$;
• любая нявыраджаная квадратная матрыца — са сваёй адваротнай матрыцай: ${\displaystyle \mathbf {AA^{-1}} =\mathbf {A^{-1}A} =\mathbf {E} }$.

Вызначнік і след здабытку не залежаць ад парадку множання матрыц:

${\displaystyle \det(\mathbf {AB} )=\det(\mathbf {BA} )=\det \mathbf {A} \cdot \det \mathbf {B} ;}$

${\displaystyle {\mbox{tr}}(\mathbf {AB} )={\mbox{tr}}(\mathbf {BA} ).}$

Адваротная матрыца

Асноўны артыкул: Адваротная матрыца

Квадратная матрыца ${\displaystyle A}$ называецца неасаблівай (нявыраджанай), калі яна мае адзіную адваротную матрыцу ${\displaystyle A^{-1}}$ такую, што выконваецца ўмова:

${\displaystyle AA^{-1}=A^{-1}A=E.}$

У адваротным выпадку матрыца ${\displaystyle A}$ называецца асаблівай (выраджанай).

Матрыца ${\displaystyle A=\left[a_{ik}\right]}$ парадку ${\displaystyle n}$ з’яўляецца нявыраджанай тады і толькі тады, калі ${\displaystyle \det A=\det \left[a_{ik}\right]\neq 0;}$ у гэтым выпадку ${\displaystyle A^{-1}}$ ёсць квадратная матрыца таго ж парадку ${\displaystyle n:}$

${\displaystyle A^{-1}=\left[a_{ik}\right]^{-1}=\left[{\frac {A_{ki}}{\det A}}\right],}$

дзе ${\displaystyle A_{ik}}$ — алгебраічнае дапаўненне элемента ${\displaystyle a_{ik}}$ у вызначніку ${\displaystyle \det \left[a_{ik}\right].}$

Алгарытмы хуткага перамнажэння матрыц

Складанасць вылічэння здабытку матрыц па азначэнні складае ${\displaystyle \ O(n^{3})}$, аднак існуюць больш эфектыўныя алгарытмы^[1], якія прымяняюцца для вялікіх матрыц. Пытанне пра мяжу хуткасці множання вялікіх матрыц, гэтак жа як і пытанне пра стварэнне найбольш хуткіх і ўстойлівых практычных алгарытмаў множання вялікіх матрыц застаецца адной з нераскрытых праблем лінейнай алгебры.

• Алгарытм Штрассена (1969)

Першы алгарытм хуткага множання вялікіх матрыц быў распрацаваны Фолькерам Штрасенам^[2] у 1969 годзе. У аснове алгарытму ляжыць рэкурсіўная разбіўка матрыц на блокі 2×2. Штрасен даказаў, што матрыцы 2×2 можна некамутатыўна перамножыць з дапамогай сямі множанняў, таму на кожным этапе рэкурсіі выконваецца сем множанняў замест васьмі. У выніку асімптатычная складанасць гэтага алгарытму складае ${\displaystyle O(n^{\log _{2}7})\approx O(n^{2.81})}$. Недахопам гэтага метаду з’яўляецца большая складанасць праграмавання ў параўнанні са стандартным алгарытмам, слабая лікавая ўстойлівасць і большы аб’ём выкарыстанай памяці. Распрацаваны шэраг алгарытмаў на аснове метаду Штрасена, якія паляпшаюць лікавую ўстойлівасць, хуткасць па канстанце і іншыя яго характарыстыкі. Тым не менш, з-за прастаты алгарытм Штрасена застаецца адным з практычных алгарытмаў множання вялікіх матрыц. Штрасен таксама вылучыў наступную гіпотэзу Штрасена: для якой заўгодна малой ${\displaystyle \varepsilon >0}$ існуе алгарытм, пры дастаткова вялікіх натуральных n гарантуе перамнажэнне дзвюх матрыц памеру ${\displaystyle n\times n}$ за ${\displaystyle O(n^{2+\varepsilon })}$ аперацый.

• Далейшыя паляпшэнні паказчыка ступені ω для хуткасці матрычнага множання

Храналогія паляпшэння ацэнак паказчыка ступені ω для вылічальнай складанасці матрычнага множання ${\displaystyle O(n^{\omega })}$.

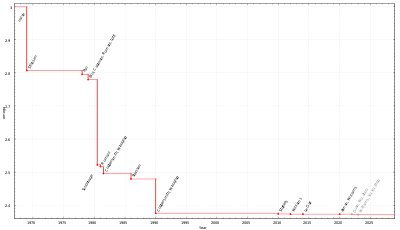
У далейшым ацэнкі хуткасці множання вялікіх матрыц шматразова паляпшаліся. Аднак гэтыя алгарытмы насілі тэарэтычны, галоўным чынам набліжаны характар. З-за неўстойлівасці алгарытмаў набліжанага множання ў цяперашні час яны не выкарыстоўваюцца на практыцы.

• Алгарытм Пана (1978)

У 1978 годзе Пан^[3] прапанаваў свой метад множання матрыц, складанасць якога склала Θ(n^2.78041).

• Алгарытм Біні (1979)

У 1979 годзе група італьянскіх навукоўцаў на чале з Біні^[4] распрацавала алгарытм множання матрыц з выкарыстаннем тэнзараў. Яго складанасць складае Θ(n^2.7799).

• Алгарытмы Шонхаге (1981)

У 1981 годзе Шонхаге^[5] прадставіў метад, які працуе з хуткасцю Θ(n^2.695). Ацэнка атрымана з дапамогай падыходу, названага частковым матрычным множаннем. Пазней яму ўдалося атрымаць ацэнку Θ(n^2.6087).

Затым Шонхаге на базе метаду прамых сум атрымаў ацэнку складанасці Θ(n^2.548). Рамані змог панізіць ацэнку да Θ(n^2.5166), а Пан — да Θ(n^2.5161).

• Алгарытм Каперсміта — Вінаграда (1990)

У 1990 годзе Копперсміт і Вінаград^[6] апублікавалі алгарытм, асімптатычная складанасць якога складала O(n^2.3755). Гэты алгарытм выкарыстоўвае ідэі, падобныя з алгарытмам Штрасена. На сённяшні дзень мадыфікацыі алгарытму Каперсміта—Вінаграда з’яўляюцца найбольш асімптатычна хуткімі. У апошняй мадыфікацыі (2024) складанасць алгарытму складае O(n^2.371552). Вядома, што шырокі клас мадыфікацый гэтага алгарытму ў прынцыпе не можа дасягнуць складанасці лепшай, чым O(n^2.3078)^[7]. Алгарытм Копперсміта—Вінаграда эфектыўны толькі на матрыцах астранамічнага памеру і на практыцы прымяняцца не можа.

• Сувязь з тэорыяй груп (2003)

У 2003 годзе Кох і інш. разгледзелі ў сваіх працах^[8] алгарытмы Штрасена і Каперсміта-Вінаграда ў кантэксце тэорыі груп. Яны паказалі, што гіпотэза Штрасена справядлівая (г. зн. мінімальная складанасць абмежаваная ${\displaystyle O(n^{2+\varepsilon })}$ для любога ${\displaystyle \varepsilon }$), калі выконваецца адна з гіпотэз тэорыі груп^[9].

Ступені матрыц

Квадратныя матрыцы можна шмат разоў множыць самі на сябе гэтак жа, як звычайныя лікі, паколькі ў іх аднолькавая колькасць радкоў і слупкоў. Такое паслядоўнае множанне можна назваць узвядзеннем матрыцы ў ступень — гэта будзе прыватным выпадкам звычайнага множання некалькіх матрыц. У прамавугольных матрыц колькасць радкоў і слупкоў розная, таму іх ніколі нельга ўзводзіць у ступень.

Матрыца A памеру n × n, узведзеная ў ступень, вызначаецца формулай

${\displaystyle \mathbf {A} ^{k}=\underbrace {\mathbf {A} \mathbf {A} \cdots \mathbf {A} } _{k}}$

і валодае наступнымі ўласцівасцямі (λ — некаторы скаляр):

Нулявая ступень:

${\displaystyle \mathbf {A} ^{0}=\mathbf {E} }$

дзе E — адзінкавая матрыца. Гэта аналаг таго факту, што нулявая ступень любога ліку роўная адзінцы.

Множанне на скаляр:

${\displaystyle (\lambda \mathbf {A} )^{k}=\lambda ^{k}\mathbf {A} ^{k}}$

Вызначнік:

${\displaystyle \det(\mathbf {A} ^{k})=\det(\mathbf {A} )^{k}}$

Найбольш просты спосаб вылічэння ступені матрыцы — гэта множыць k разоў матрыцу A на вынік папярэдняга множання, пачынаючы з адзінкавай матрыцы, як гэта часта робяць для скаляраў. Для дыяганалізуемых матрыц існуе лепшы метад, заснаваны на выкарыстанні спектральнага раскладанне матрыцы A. Яшчэ адзін метад, заснаваны на тэарэме Гамільтана — Кэлі, будуе больш эфектыўнае выражэнне для A^k, у якім у патрабаваную ступень узводзіцца скаляр, а не ўся матрыца.

Асобны выпадак складаюць дыяганальныя матрыцы. Паколькі здабытак дыяганальных матрыц зводзіцца да множання адпаведных дыяганальных элементаў, то k-ая ступень дыяганальнай матрыцы A складаецца з элементаў, узведзеных у патрабаваную ступень:

${\displaystyle \mathbf {A} ^{k}={\begin{pmatrix}a_{11}&0&\cdots &0\\0&a_{22}&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &a_{nn}\end{pmatrix}}^{k}={\begin{pmatrix}a_{11}^{k}&0&\cdots &0\\0&a_{22}^{k}&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &a_{nn}^{k}\end{pmatrix}}.}$

Такім чынам, узвесці дыяганальную матрыцу ў ступень нескладана. Пры ўзвядзенні адвольнай матрыцы (не абавязкова дыяганальнай) у ступень часта аказваецца карысным выкарыстоўваць спачатку ўласцівасці дыяганалізуемых матрыц.

Выкарыстоўваючы множанне матрыц і ўзвядзенне матрыц у ступень, можна вызначыць іншыя аперацыі над матрыцамі. Напрыклад, матрычная экспанента можа быць вызначана праз ступеневы рад, матрычны лагарыфм — як адваротная да матрычнай экспаненты функцыя і гэтак далей.

Гл. таксама

• Здабытак Кронекера
• Здабытак Адамара

Літаратура

• Корн Г., Корн Т. Алгебра матриц и матричное исчисление // Справочник по математике (руск.). — 4-е издание. — М: Наука, 1978. — С. 392—394.

Крыніцы

1. Кибернетический сборник. Новая серия. Вып. 25. Сб. статей 1983—1985 гг.: Пер. с англ. — М.: Мир, 1988 — В. Б. Алекссев. Сложность умножения матриц. Обзор.
2. Strassen V. Gaussian Elimination is not Optimal // Numer. Math / F. Brezzi — Springer Science+Business Media, 1969. — Vol. 13, Iss. 4. — P. 354–356. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF02165411
   <a href="https://wikidata.org/wiki/Track:Q65212"></a><a href="https://wikidata.org/wiki/Track:Q1442541"></a><a href="https://wikidata.org/wiki/Track:Q7069670"></a><a href="https://wikidata.org/wiki/Track:Q176916"></a><a href="https://wikidata.org/wiki/Track:Q21694537"></a>
3. Pan V. Ya, Strassen’s algorithm is not optimal — trilinear technique of aggregating uniting and canceling for constructing fast algorithms for matrix operations. — Proc. 19th Annual Symposium on Foundations of Computer Science, Ann Arbor, Mich., 1978
4. Bini D., Capovani M., Lotti G., Romani F. — ${\displaystyle O(n^{2.7799})}$ complexity for approximate matrix multiplication. — Inform. Process. Lett., 1979
5. Schonhage A. Partial and total matrix multiplication. — SIAM J. Comput., 1981
6. Don Coppersmith and Shmuel Winograd. Matrix multiplication via arithmetic progressions. Journal of Symbolic Computation, 9:251-280, 1990.
7. New Breakthrough Brings Matrix Multiplication Closer to Ideal (нявызн.). Quanta Magazine. Праверана 7 сакавіка 2024.
8. Group-theoretic Algorithms for Matrix Multiplication (нявызн.). Архівавана з першакрыніцы 6 жніўня 2011. Праверана 26 верасня 2009.
9. Toward an Optimal Algorithm for Matrix Multiplication (нявызн.)(недаступная спасылка). Архівавана з першакрыніцы 31 сакавіка 2010. Праверана 26 верасня 2009.