Поляризатор

Поляризатор е оптичен филтър, който пропуска светлинни вълни с определена поляризация, като същевременно блокира светлинни вълни с други поляризации. [1] [2] [3] [4] Той може да преобразува лъч светлина с неопределена или смесена поляризация в лъч с добре дефинирана поляризация, тоест използва се за получаване на поляризирана светлина. Често срещаните видове поляризатори са линейни поляризатори и кръгови поляризатори. Поляризаторите се използват в много оптични техники и инструменти, а поляризационните филтри намират приложение във фотографията и LCD технологията. Поляризатори могат да бъдат направени и за други видове електромагнитни вълни освен за видимата светлина, като радиовълни, микровълни и рентгенови лъчи.
Линейни поляризатори
[редактиране | редактиране на кода]Линейните поляризатори могат да бъдат разделени на две основни категории: абсорбиращи поляризатори, при които нежеланите състояния на поляризация се абсорбират от устройството, и поляризатори с разделяне на лъча, при които неполяризираният лъч се разделя на два лъча с противоположни състояния на поляризация. Поляризатори, които поддържат едни и същи оси на поляризация при различни ъгли на падане често се наричат Декартови поляризатори, тъй като поляризационните вектори могат да бъдат описани с прости декартови координати (например хоризонтални спрямо вертикални), независими от ориентацията на повърхността на поляризатора. Когато двете поляризационни състояния се съотнесат към посоката на повърхността (обикновено при отражение), те обикновено се наричат s и p поляризация. Това разграничение между декартова и s – p поляризация може да бъде незначително в много случаи, но става важно за постигане на висок контраст и при широкоъглов обхват на падащата светлина.
Поляризация при отражение
[редактиране | редактиране на кода]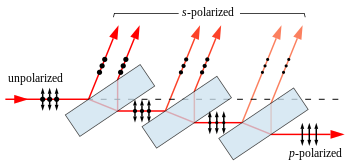
Когато светлината се отразява под ъгъл от границата между два прозрачни материала (описва се с формулите на Френел), отражението е различно за лъч светлина, поляризиран в равнината на падане, и лъч, поляризиран перпендикулярно на нея. Светлината, поляризирана в равнината, се нарича p -поляризирана, докато тази поляризирана перпендикулярно на нея е s -поляризирана. Под специален ъгъл, известен като ъгъл на Брюстер, p-поляризираната светлина не се отразява от повърхността, следователно цялата отразена светлина трябва да бъде s-поляризирана, с електрическо поле, перпендикулярно на равнината на падане.
Поляризатори с двойно лъчепречупване
[редактиране | редактиране на кода]Други линейни поляризатори използват двойнопречупващите свойства на кристали като кварц и калцит. В тези кристали лъч неполяризирана светлина, падащ върху повърхността, се разделя чрез пречупване на два лъча. Законът на Снелиус важи и за двата лъча, обикновения или o-лъч, и необикновения или н-лъч, като всеки лъч има различен показател на пречупване (двойно лъчепречупване). Като цяло двата лъча ще бъдат в различни състояния на поляризация, макар и не линейна, с изключение на определени посоки на разпространение спрямо кристалната ос.

Един от първите такива поляризатори е призмата на Никол. Тя се състои от кристал от калцит, който е бил разцепен и отново съединен с канадски балсам. Кристалът е изрязан под специален ъгъл така, че o- и н- лъчите да са в състояния на ортогонална линейна поляризация. Пълното вътрешно отражение на обикновения лъч възниква на повърхността на балсама, тъй като той има по-голям показател на пречупване в калцита, отколкото в балсама, и лъчът се отклонява към кристала. Необикновеният лъч, който има по-малък показател на пречупване в калцита, се предава през границата без отклонение. Призмите на Никол произвеждат поляризирана светлина с много висока чистота и са широко използвани в микроскопията, въпреки че в съвременната употреба са заменени предимно с алтернативи като призмата на Глан–Томпсън, призмата на Глан–Фуко и призмата на Глан–Тейлър. Тези призми не са истински поляризиращи лъчеделители, тъй като напълно поляризиран е само преминалият лъч.

Призмата на Уоластън е друг двойнопречупващ поляризатор, състоящ се от две триъгълни калцитни призми с ортогонални кристални оси, които са залепени заедно. На вътрешната граница всеки неполяризиран лъч се разделя на два линейно поляризирани лъча, които напускат призмата под ъгъл на отклонение от 15° до 45°. Призмите на Рошон и Сенармон са подобни, но използват различни ориентации на оптичните оси в двете призми. Призмата на Сенармон е с въздушно разстояние, за разлика от призмите на Уоластън и Рошон. Тези призми наистина разделят лъча на два напълно поляризирани лъча с перпендикулярни поляризации. Призмата на Номарски е вариант на призмата на Уоластън, която се използва широко в диференциалната интерференчна контрастна микроскопия.
Закон на Малус и други свойства
[редактиране | редактиране на кода]
Законът на Малус, който е кръстен на Етиен-Луи Малус, гласи, че когато поляризиран лъч светлина преминава през идеален поляризатор, интензитетът I на преминалата светлина, се дава от
където I 0 е началният интензитет и θ i е ъгълът между първоначалната посока на поляризация на светлината и оста на поляризатора.
Лъч неполяризирана светлина може да се разглежда като съдържащ разнородна смес от линейни поляризации под всички възможни ъгли. Тъй като средната стойност на е 1/2, коефициентът на предаване става
На практика в поляризатора има загуби и действителното предаване ще бъде малко по-ниско от това, около 38% за поляризатори тип Полароид, но значително по-високо (>49,9%) за някои типове двойнопречупващи призми.
Ако два поляризатора са поставени един след друг (вторият поляризатор обикновено се нарича анализатор), взаимният ъгъл между техните поляризационни оси дава стойността на θ в закона на Малус. Ако двете оси са ортогонални, поляризаторите са кръстосани и на теория светлината се блокира (погасява). Въпреки това, нито един поляризатор не е перфектен и затова пропускането не е точно нула (например кръстосаните листове Polaroid изглеждат леко сини на цвят, защото погасяват по-добре червеното). Ако прозрачен обект се постави между кръстосани поляризатори, всички поляризационни ефекти, налични в пробата (като двойно пречупване), ще се проявят като увеличение на предаването. Този ефект се използва в поляриметрията за измерване на оптичната активност на пробата.
Кръгови поляризатори
[редактиране | редактиране на кода]Кръговите поляризатори (кръгови поляризиращи филтри) могат да се използват за създаване на кръгова поляризирана светлина или алтернативно за селективно абсорбиране или пропускане на кръгова поляризирана светлина по посока на часовниковата стрелка и обратно на часовниковата стрелка. Те се използват като поляризиращи филтри във фотографията за намаляване на паразитните отражения от неметални повърхности и се използват като лещи в 3D очилата, използвани за гледане на някои стереоскопични филми (по-специално разновидността RealD 3D), където поляризацията се използва за разграничаване на това, кое изображение да се вижда с лявото и дясното око.
Вижте също
[редактиране | редактиране на кода]- Поляриметър
- Микроскоп с поляризирана светлина
Източници
[редактиране | редактиране на кода]- ↑ Wolf, Mark J. P. The Video Game Explosion: A History from PONG to Playstation and Beyond. ABC-CLIO, 2008. ISBN 978-0313338687. с. 315.
- ↑ Johnsen, Sönke. The Optics of Life: A Biologist's Guide to Light in Nature. Princeton Univ. Press, 2012. ISBN 978-0691139913. с. 207 – 208.
- ↑ Basu, Dipak. Dictionary of Pure and Applied Physics. CRC Press, 2000. ISBN 1420050222. с. 142 – 143.
- ↑ Gåsvik, Kjell J. Optical Metrology. 3rd. John Wiley and Sons, 2003. ISBN 0470846704. с. 219 – 221.
| Тази страница частично или изцяло представлява превод на страницата Polarizer в Уикипедия на английски. Оригиналният текст, както и този превод, са защитени от Лиценза „Криейтив Комънс – Признание – Споделяне на споделеното“, а за съдържание, създадено преди юни 2009 година – от Лиценза за свободна документация на ГНУ. Прегледайте историята на редакциите на оригиналната страница, както и на преводната страница, за да видите списъка на съавторите.
ВАЖНО: Този шаблон се отнася единствено до авторските права върху съдържанието на статията. Добавянето му не отменя изискването да се посочват конкретни източници на твърденията, които да бъдат благонадеждни. |


