Хипотрохоида

Конструкция на хипотрохоида при R = 1, r = 0.6, d = 1.2

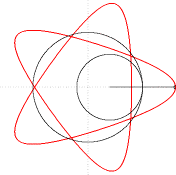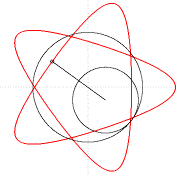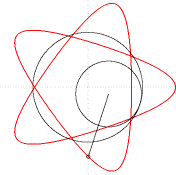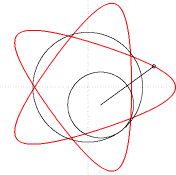
В геометрията хипотрохоида е равнинна трансцендентна крива, описана от точка фиксирана спрямо окръжност, която се търкаля по вътрешната страна на друга, направляваща, окръжност, с радиус равен или по-голям от радиуса на първата.

Класификация и уравнение

Фиксирането на точката спрямо малката окръжност става с прекарване на отсечка, която свързва точката с центъра на окръжността. Взимат се под внимание два параметъра: d – дължината на получената отсечка и r – радиус на малката окръжност. В зависимост от отношението между тях разглеждаме:

• скъсена хипотрохоида – при d < r, т.е. когато точката е вътрешна за окръжността;
• хипоциклоида – при d = r, т.е. когато точката принадлежи на окръжността;
• удължена хипотрохоида – при d > r, т.е. когато точката е външна за окръжността.

Специален случай на хипотрохоида е окръжността, при R = 2r.

Нека използваме горните означения, като добавим само R – радиус на направляващата окръжност. Тогава параметричните уравнения на хипотрохоидата са:

${\displaystyle {\begin{cases}x(\theta )=(R-r)\cos \theta -d\ cos({\frac {R-r}{r}}\theta )\\y(\theta )=(R-r)\sin \theta -d\ sin({\frac {R-r}{r}}\theta )\end{cases}}}$,

където ${\displaystyle \theta }$ е ъгълът, образуван от абсцисната ос и правата свързваща центровете на двете окръжности.

Вижте също

• Епитрохоида
• Трохоида
• Хипоциклоида
• Циклоида

Източници

• „Лексикон Математика“, Георги Симитчиев, Георги Чобанов, Иван Чобанов, ИК Абагар, София, 1995, ISBN 954-584-146-Х
• „Физико-математическа и техническа енциклопедия“, Издателство на БАН, София, 1990
• „Математически енциклопедичен речник“, В. Гелерт, Х. Кестнер, З. Нойбер, ДИ Наука и изкуство, София, 1983

Външни препратки

• Страница за хипотрохоидата на сайта на Система Mathematica
• Java аплет, изобразяващ хипотрохоидата интерактивно Архив на оригинала от 2006-09-16 в Wayback Machine.
• Галерия от хипотрохоиди