Ъглова честота

Ъгловата честота ω (в радиани за секунда) е 2π пъти по-голяма от честотата ν (в периоди за секунда, Hz).

Сфера се върти около ос. Точките по-далече от оста се движат по-бързо, което удовлетворява равенството ω=v/r.

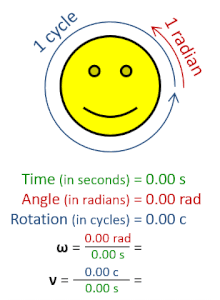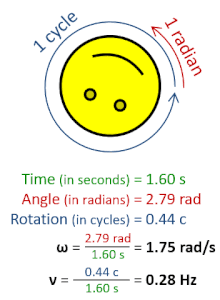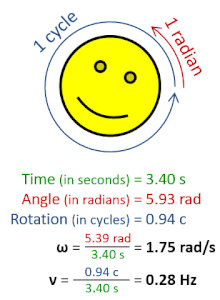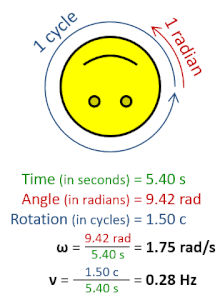
Ъглова честота (ω) е скаларна величина за скорост на въртене. Отнася се за ъгловото отместване за единица време (например при ротация) или за скоростта на промяна на фазата в синусоидална форма на вълната (например при трептения и вълни) или за скоростта на промяна на аргумента на синусоидална функция.

Ъгловата честота представлява големината на вектора на ъглова скорост.^[1] Един оборот е равен на 2π радиана и следователно:^[1][2]

${\displaystyle \omega ={{2\pi } \over T}={2\pi f},}$

където:

ω е ъгловата честота (rad/s),

T е периодът (s),

f е честотата (Hz или ν).

Мерни единици

Мерната единица по SI за ъглова честота обикновено е радиани в секунда (rad/s), дори когато тя не изразява ротационна стойност. От гледна точка на анализа на размерностите, единицата херц (Hz) също е правилна, но на практика се използва само за обикновена честота f и почти никога за ω. Тази конвенция помага да се избягват обърквания.^[3]

В цифровата обработка на сигнали ъгловата честота може да се нормализира чрез дискретизация, което дава нормализирана честота.

Кръгово движение

 Основна статия: Кръгово движение

При въртящ се или орбитиращ обект съществува връзка между разстоянието от оста, тангенциалната скорост и ъгловата честота на въртене:

${\displaystyle \omega =v/r.}$

Трептение на пружина

Обект, закачен за пружина подлежи на трептение. Ако пружината се счита за идеална, незатихваща и без маса, тогава движението е просто и хармонично с ъглова честота, изведена чрез:^[4]

${\displaystyle \omega ={\sqrt {\frac {k}{m}}},}$

където

k е пружинната константа,

m е масата на обекта,

ω е естествената честота (която понякога бива отбелязвана и с ω₀.)

Докато обектът трепти, неговото ускорение се изчислява чрез

${\displaystyle a=-\omega ^{2}x,}$

където x е преместването от точката на равновесие.

Използвайки обикновена честота от обороти в секунда, това уравнение приема вида

${\displaystyle a=-4\pi ^{2}f^{2}x.}$

LC вериги

Резониращата ъглова честота в LC верига с последователно свързване е равна на квадратния корен от реципрочното на произведението на капацитета (C) и индуктивността (L):^[5]

${\displaystyle \omega ={\sqrt {\frac {1}{LC}}}.}$

Свързването последователно на съпротивление (например, поради съпротивление на навивките в намотка) не променя резониращата честота на последователната LC верига. За паралелно свързана верига, горното уравнение често е полезно приближение, но резониращата честота не зависи от загубите на елементите, които са свързани паралелно.

Вижте също

• Ъглова скорост

Източници

1. Cummings, Karen. Understanding physics. New Delhi, John Wiley & Sons Inc., authorized reprint to Wiley – India, 2007. ISBN 978-81-265-0882-2. с. 449, 484, 485, 487.
2. Holzner, Steven. Physics for Dummies. Hoboken, New Jersey, Wiley Publishing Inc, 2006. ISBN 978-0-7645-5433-9. с. 201.
3. Lerner, Lawrence S. Physics for scientists and engineers. 1 януари 1996. ISBN 978-0-86720-479-7. с. 145.
4. Serway, Raymond A. Principles of physics. 4th. Belmont, CA, Brooks / Cole – Thomson Learning, 2006. ISBN 978-0-534-46479-0. с. 375, 376, 385, 397.
5. Nahvi, Mahmood. Schaum's outline of theory and problems of electric circuits. McGraw-Hill Companies (McGraw-Hill Professional), 2003. ISBN 0-07-139307-2. с. 214, 216.(LC1)