কুইক সর্ট
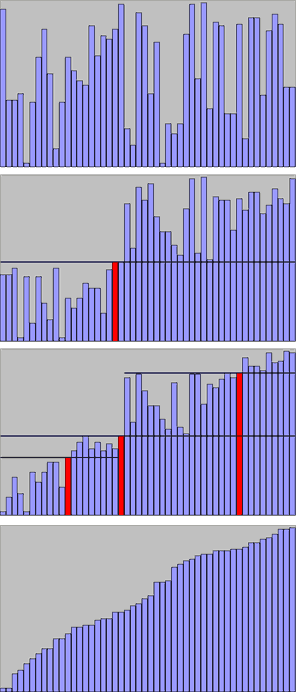
কুইক সর্ট একটি সুপরিচিত সর্টিং অ্যালগোরিদম। টোনি হোর ১৯৬০ সালে এটি উদ্ভাবন করেন। এই সর্টিং অ্যালগোরিদমটি n সংখ্যক জিনিসকে সর্ট করতে বা নির্দিষ্ট ক্রমে সাজাতে গড়ে Θ(n log n) সংখ্যক তুলনা(comparisons) করে থাকে। তবে ওয়ার্স্ট কেসে অরথাত সব থেকে প্রতিকুল অবস্থায় অ্যালগোরিদমটি O(n2) সংখ্যক তুলনা করে থাকে। সাধারণভাবে, কুইক সর্ট অন্যান্য Θ(n log n) সর্টিং অ্যালগোরিদমগুলির চেয়ে উল্লেখযোগ্যপরিমাণ দ্রুততর, কারণ এর ভেতরের লুপটি বেশির ভাগ নির্মাণ-কৌশলে সুবিধাজনকভাবে বাস্তবায়ন করা যায় এবং বাস্তব জীবনে ব্যবহৃত বেশির ভাগ উপাত্তের জন্য নকশাটি এমনভাবে বেছে নেয়া যায় যাতে দ্বি-ঘাত সময় এড়ানো সম্ভবপর হয়। কুইক সর্ট একরকমের তুলনাকেন্দ্রিক সর্ট। সুবিধাজনক বাস্তবায়নে এটা আর সুস্থিত সর্ট থাকে না।
অ্যালগোরিদম
[সম্পাদনা]
কুইক সর্ট বিভক্ত কর এবং জয় কর কৌশলে সর্ট করে থাকে, এজন্য একটা বড় তালিকাকে এটি দুটি ক্ষুদ্রতর তালিকায় বিভক্ত করে।
ধাপগুলি হলোঃ
- তালিকা থেকে পিভট নামক একটি সদস্য বাছাই কর।
- তালিকাটিকে পুনরায় নির্দিষ্ট ক্রমে এমনভাবে সাজাও যাতে পিভট থেকে ছোট তালিকাস্থ সকল সদস্য পিভটের আগে থাকে আর পিভটের চেয়ে বড় সকল সদস্য থাকে পিভটের পরে(পিভটের সমমানের সদস্য আগে বা পরে যেকোন জায়গায় থাকতে পারে)। এই পার্টিশনকরণের শেষে পিভট তার চূড়ান্ত অবস্থানে (সঠিকভাবে ক্রমক্রীত তালিকায় তার যেখানে থাকার কথা সেখানে) থাকবে। এটাকে পার্টিশন ক্রিয়া বলা হয়ে থাকে।
- পুনরাবৃত্তভাবে পিভট অপেক্ষা ক্ষুদ্রতর মানবিশিষ্ট সদস্যদের উপতালিকা এবং বৃহত্তর মানবিশিষ্ট সদস্যদের উপতালিকাকে সর্ট কর।
পুনরাবৃত্তির বেস কেইস বা ভিত্তি অবস্থা হচ্ছে শূন্য বা একক দৈর্ঘ্যের তালিকা যারা আপনা থেকেই সর্টকৃত থাকে। অ্যালগোরিদমটির ইনপুট যদি সসীম একটি তালিকা হয়ে থাকে তাহলে এটি সসীম সময়েই তালিকাটিকে সর্ট করতে পারবে, কারণ প্রতি ইটারেশনে এটি কমপক্ষে একটা সদস্যকে তার চূড়ান্ত অবস্থানে স্থাপন করতে সমর্থ হয়।
সহজ স্যুডোকোডে প্রকাশ করলে অ্যালগরিদমটি হবেঃ
function quicksort(q)
var list less, pivotList, greater
if length(q) ≤ 1
return q
select a pivot value pivot from q
for each x in q except the pivot element
if x < pivot then add x to less
if x ≥ pivot then add x to greater
add pivot to pivotList
return concatenate(quicksort(less), pivotList, quicksort(greater))
উল্লেখ্য যে, কোন একটা সদস্যকে পর্যবেক্ষণে অন্যান্য সদস্যের সাথে এর তুলনাকেই কেবল ব্যবহার করা হয়েছে বলে কুইক সর্ট একধরনের তুলনাকেন্দ্রিক সর্ট।
ফাংশনাল ভাষাগুলোতে সাধারণত অ্যালগোরিদমগুলো হুবহু লেখা যায়, যেমন হ্যাস্কেলে অ্যালগোরিদমটি হলো:
quickSort [] = []
quickSort (x : xs) = quickSort lower ++ equal ++ quickSort higher
where lower = filter (< x) xs
equal = x : (filter (== x) xs)
higher = filter (> x) xs
অন্তর্গত পার্টিশনযুক্ত সংস্করণ
[সম্পাদনা]পারফরমেন্সের পূর্ণ বিবরণ
[সম্পাদনা]উৎকৃষ্টতর পিভট ব্যবহার
[সম্পাদনা]পার্টিশনের বিষয়াবলী
[সম্পাদনা]অন্যান্য মিতব্যয়ীতা
[সম্পাদনা]ছোট তালিকার জন্যে ভিন্ন অ্যালগোরিদম ব্যবহার
[সম্পাদনা]ওয়ার্স্ট-কেইস স্মৃতি-ব্যবহার কমানো
[সম্পাদনা]সমান্তরাল-করণ
[সম্পাদনা]"ভাগ করে জয় কর " এই পদ্ধতির জন্য মার্জ শর্ট এর মত কুইক শর্টকেও সমান্তরাল-করণ করা যায় |
প্রতিদ্বন্দী সর্টিং অ্যালগোরিদম
[সম্পাদনা]গাণিতিক বিশ্লষণ
[সম্পাদনা]এলোমেলোকৃত কুইক সর্টের প্রত্যাশিত জটিলতা
[সম্পাদনা]গড় জটিলতা
[সম্পাদনা]স্থানিক জটিলতা
[সম্পাদনা]বাছাইকরণের সাথে সম্পর্ক
[সম্পাদনা]বহিঃসংযোগ
[সম্পাদনা]উৎসপঞ্জী
[সম্পাদনা]পাদটীকা
[সম্পাদনা]| এই নিবন্ধটি অসম্পূর্ণ। আপনি চাইলে এটিকে সম্প্রসারিত করে উইকিপিডিয়াকে সাহায্য করতে পারেন। |