কেপলার ত্রিভুজ

কেপলার ত্রিভুজ হলো এমন একটি সমকোণী ত্রিভুজ যা সোনালি অনুপাতভিত্তিক একটি গুণোত্তর প্রগমনের অন্তর্ভুক্ত তিনটি বর্গের মাধ্যমে গঠিত হয়।

কেপলার ত্রিভুজ হলো এমন একটি বিশেষ সমকোণী ত্রিভুজ যার বাহু তিনটির দৈর্ঘ্য একটি গুণোত্তর প্রগমন গঠন করে, যেখানে এই প্রগমনের সাধারণ অনুপাত হলো ${\displaystyle {\sqrt {\varphi }}}$ এবং ${\displaystyle \varphi =(1+{\sqrt {5}})/2}$ হলো সোনালি অনুপাত। কেপলার ত্রিভুজের অনন্য বৈশিষ্ট এই প্রগমনটিকে ${\displaystyle 1:{\sqrt {\varphi }}:\varphi }$ আকারে অথবা, আনুমানিকভাবে 1 : 1.272 : 1.618 আকারেও লেখা যায়। কেপলার ত্রিভুজের বাহুগুলোর ওপর অঙ্কিত বর্গ তিনটির ক্ষেত্রফল পৃথক আরেকটি গুণোত্তর প্রগমন গঠন করে। এটি হচ্ছে ${\displaystyle 1:\varphi :\varphi ^{2}}$। একই ত্রিভুজের বিকল্প সংজ্ঞার ক্ষেত্রে, দুটি সংখ্যার তিনটি পিথাগোরাসীয় গড়ের শর্তালোকে অথবা, সমদ্বিবাহু ত্রিভুজের অন্তর্ব্যাসার্ধের মাধ্যমে এই ত্রিভুজের বৈশিষ্ট্য নির্ধারণ করা হয়।

জ্যোতির্বিদ জোহানেস কেপলারের নামানুসারে এই ত্রিভুজের নামকরণ করা হলেও তার পূর্বেকার নথি বা সূত্রগুলোতেও এর অস্তিত্ব পাওয়া যায়। কিছু সূত্র মোতাবেক প্রাচীন মিশরীয় পিরামিডগুলোতে কেপলার ত্রিভুজভিত্তিক অনুপাত থাকার দাবি করা হলেও, মিশরীয় গণিত ও স্থাপত্যবিদ্যায় সোনালি অনুপাত অজানা ছিল বলেই অধিকাংশ পণ্ডিতের বিশ্বাস।

ইতিহাস

জার্মান গণিতবিদ ও জ্যোতির্বিজ্ঞানী জোহানেস কেপলারের (১৫৭১-১৬৩০) নাম অনুসারে এই ত্রিভুজটির নাম কেপলার ত্রিভুজ রাখা হয়েছে। কেপলার ১৬৯৭ সালে একটি চিঠিতে এই জ্যামিতিক কাঠামোটি নিয়ে লেখেন।^[১] যে দুটি ধারণার আলোকে এই ত্রিভুজটি বিশ্লেষণ করা যেতে পারে সেগুলোর উভয়েই ছিল কেপলারের আগ্রহের বিষয়। এই ধারণা দুটি হলো পিথাগোরাসের উপপাদ্য ও সোনালি অনুপাত। তারই ভিন্ন আরেকটি লেখা থেকে তার এই আগ্রহের অনুমান পাওয়া যায়:

জ্যামিতির দুটি বিশাল ধন-ভাণ্ডার রয়েছে: একটি হল পিথাগোরাসের উপপাদ্য, অন্যটি হলো পরম ও গড় অনুপাতে একটি রেখার বণ্টন। প্রথমটিকে আমরা তুলনা করতে পারি বিশাল স্বর্ণ খণ্ডের সাথে, আর দ্বিতীয়টিকে বলা যেতে পারে মূল্যবান রত্ন।^[২]

সে যাই হোক, কেপলারই যে প্রথম এই ত্রিভুজের বিবরণ দিয়েছিলেন তা কিন্তু নয়।^[৩] স্বয়ং কেপলার এটার কৃতিত্ব দিয়েছেন ম্যাগিরাস নাম্নী (সঙ্গীতের) এক অধ্যাপককে।^[১] আবু বকরের লেখা আরবি গণিতের একটি বইয়ের ল্যাটিন অনুবাদ হলো Liber mensurationum, যা ১২শ শতকে ইটালীয় অনুবাদক জেরার্ড অব ক্রেমোনা কর্তৃক অনুদিত হয়। এই বইয়েও একই ত্রিভুজের উল্লেখ পাওয়া যায়।^[৩][৪] উপরন্তু, ১২২০-২১ সালে ফিবোনাচ্চির প্রকাশিত প্রাকতিকা জিওমেত্রিয়াতেও (Practica geometriae [it]) এই ত্রিভুজের বিবরণ পাওয়া যায়। কেপলার যেভাবে এই ত্রিভুজকে সংজ্ঞায়িত করেছেন ফিবোনাচ্চিও সেইভাবে একে সংজ্ঞায়িত করেছেন।^[৩][৫] কেপলারের কিছু আগে প্রায় ১৫৬৭ সালের দিকে পর্তুগিজ গণিতবিদ পেড্রো নুনেসও এটি নিয়ে লিখেছিলেন। এই বিষয়টা "শেষ মধ্যযুগ এবং রেনেসাঁ সংশ্লিষ্ট পাণ্ডুলিপি ঐতিহ্যে ব্যাপকহারে ছড়িয়ে পড়েছিল" বলা যায়।^[৩] এছাড়া, কেপলারের পরেও বেশ কয়েকবার স্বতন্ত্রভাবে এই ত্রিভুজের পুনঃআবিষ্কার ঘটেছে।^[১]

একটি একটি বর্গাকার পিরামিডের শীর্ষবিন্দু, এর ভূমির কেন্দ্রবিন্দু এবং এর একটি বাহুর মধ্যবিন্দু নিয়ে গঠিত সমকোণী ত্রিভুজ। গিজার গ্রেট পিরামিডটি যেভাবে একটি কেপলার ত্রিভুজ বলে অভিপ্রেত হয়, সেভাবেই এই ত্রিভুজটি গঠিত বলে কিছু পিরামিডতত্ত্ববিদ তত্ত্ব দিয়েছেন।

কিছু লেখকের মতে, একটি দ্বৈত কেপলার ত্রিভুজযুক্ত সোনালি পিরামিড থেকে এর প্রস্থচ্ছেদের মতোই মিশরীয় পিরামিডগুলোর (যেমন: গিজার গ্রেট পিরামিড) নকশার সঠিক ব্যাখ্যা পাওয়া যায়। যেসব বিষয়ের ওপর ভিত্তি করে এই তত্ত্ব গড়ে উঠেছে সেসবের মধ্যে ১৯শ শতকের পিরামিড-তত্ত্ববিদ জন টেইলর কর্তৃক প্রাচীন গ্রিক ইতিহাসবিদ হিরোডোটাসের ভুল পাঠও রয়েছে।^[৬][৭] কেপলার ত্রিভুজের সাথে সম্পর্ক নেই এমন অন্যান্য অনেক অনুপাত-তত্ত্বেরও প্রস্তাব করা হয়েছিল এই একই পিরামিডের জন্য।^{[১][৬][৮]} Because these different theories are very similar in the numeric values they obtain, and because of inaccuracies in measurement, in part caused by the destruction of the outer surface of the pyramid, such theories are difficult to resolve based purely on physical evidence.

^[৬][৯] কেপলার ত্রিভুজের অনুপাতের এই মিলটি বরং একটি সাংখ্যিক সমাপতনই হওয়া উচিত: কারণ এই সম্পর্কটি নিয়ে অনুসন্ধান চালিয়েছেন এমন পণ্ডিতদের মতে, খুব সম্ভবত প্রাচীন মিশরীয়রা সোনালি অনুপাত সম্পর্কে জানত না কিংবা তারা এটি তাদের গণিত বা স্থাপত্যে ব্যবহারও করত না।^{[১][৮][১০][১১]} এর পরিবর্তে, ১১ ও ১৪ একক বাহুযুক্ত একটি সমকোণী ত্রিভুজের ভিত্তিতে পূর্ণসংখ্যা অনুপাত ব্যবহার করে পিরামিডের অনুপাতকে সর্বাঙ্গরূপে ব্যাখ্যা করা যেতে পারে।^[১][৬]

১৯৭৯-এর শুরুর দিকে রজার হার্জ-ফিশলার কেপলারের ১৫৯৭ সালের চিঠির ভিত্তিতে এই জ্যামিতিক কাঠামোর জন্য "কেপলার ত্রিভুজ" নামটি ব্যবহার করেন। ১৯৪৬ সালে সোনালি অনুপাতের ওপর রোমানীয় গণিতবিদ ও দার্শনিক মাটিলা ঘিকার লেখা দ্য জিওমেট্রি অব আর্ট অ্যান্ড লাইফ নামের এক বইয়ে এই ত্রিভুজের জন্য আরেকটি নাম ব্যবহার করা হয়েছিল। এই বইয়ে পিরামিড-তত্ত্ববিদ "ডব্লিউ এ প্রাইস"-এর নামানুসারে একে "প্রাইসের ত্রিভুজ" নাম দেওয়া হয়েছে।

সংজ্ঞা

দুটি কেপলার ত্রিভুজ মিলে যখন একটি সমদ্বিবাহু ত্রিভুজ গঠিত হয়, তখন এই ত্রিভুজ দুটি এদের ক্ষুদ্র বাহুটির সাপেক্ষে একে অপরের প্রতিফলিত ত্রিভুজ হবে। দুটি কেপলার ত্রিভুজের সমন্বয়ে গঠিত এমন একটি সমদ্বিবাহু ত্রিভুজের সমান বাহু দুটির দৈর্ঘ্যের সমান দুটি বাহু নিয়ে আরও অসংখ্য সমদ্বিবাহু ত্রিভুজ গঠন করা সম্ভব (তৃতীয় বাহুর দৈর্ঘ্য ইচ্ছামত বাড়িয়ে-কমিয়ে)। তবে এই সব সমদ্বিবাহু ত্রিভুজের মধ্যে কেবল কেপলার ত্রিভুজের সমন্বয়ে গঠিত সমদ্বিবাহু ত্রিভুজেই সর্বোচ্চ দৈর্ঘ্যের অন্তর্ব্যাসার্ধ পাওয়া যাবে।

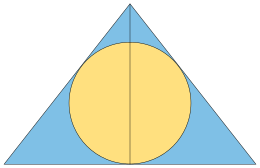
কেপলার ত্রিভুজের একটি সমকোণী ত্রিভুজ হওয়ার এবং এর বাহু তিনটি একটি গুণোত্তর প্রগমনে থাকার অথবা সমতুল্যভাবে এর বাহুগুলোর বর্গও একটি গুণোত্তর প্রগমনভুক্ত হওয়ার যে ধর্ম সেই ধর্মের মাধ্যমে কেপলার ত্রিভুজকে অনন্যভাবে সংজ্ঞায়িত করা হয়। কেপলার ত্রিভুজের বাহুগুলোর দৈর্ঘ্য যে প্রগমন গঠন করে তার সাধারণ অনুপাত হলো ${\displaystyle {\sqrt {\varphi }}}$ যেখানে, ${\displaystyle \varphi =(1+{\sqrt {5}})/2}$ হলো সোনালি অনুপাত। কেপলার ত্রিভুজের অনন্য বৈশিষ্ট এই প্রগমনটিকে ${\displaystyle 1:{\sqrt {\varphi }}:\varphi }$ আকারে অথবা, আনুমানিকভাবে 1 : 1.272 : 1.618 আকারেও লেখা যায়। প্রকৃত ঘটনা এই যে, যে ত্রিভুজে এই অনুপাতগুলো থাকে সেই ত্রিভুজটি একটি সমকোণী ত্রিভুজ হবে, যা আবার অনুসরণ করবে এই সত্যকেই যে, একটি সমকোণী ত্রিভুজের বাহুগুলোর (দৈর্ঘ্যের) বর্গ এই অনুপাতগুলো মেনে চললে, এই সমকোণী ত্রিভুজটির বাহুগুলোর বর্গের ক্ষেত্রে পিথাগোরাসের উপপাদ্যটি থেকে যে সূত্রটি (${\displaystyle \varphi ^{2}=\varphi +1}$) পাওয়া যাবে, সোনালি অনুপাতের সংজ্ঞা নির্ধারণী বহুপদীটিও হবে সেই সূত্রেরই অনুরূপ। কারণ হলো, এই সমীকরণটি সোনালি অনুপাতের জন্য সত্য, আর এই দৈর্ঘ্য তিনটি পিথাগোরাসের উপপাদ্য মেনে চলে এবং একটি সমকোণী ত্রিভুজ গঠন করে। বিপরীতভাবে বলা যায়, সমকোণী ত্রিভুজের বাহুগুলোর বর্গ সাধারণ অনুপাত ${\displaystyle \rho }$-যুক্ত একটি গুণোত্তর প্রগমন তৈরি করে এমন যেকোনো সমকোণী ত্রিভুজের ক্ষেত্রে, পিথাগোরাসের উপপাদ্যটি এই ইঙ্গিত দেয় যে, এই অনুপাতটি (${\displaystyle \rho ^{2}=\rho +1}$) অভেদকে মেনে চলে। ফলে, এই অনুপাতটি অবশ্যই উক্ত সমীকরণের অনন্য ধনাত্মক সমাধান হবে, তথা এটি হবে সোনালি অনুপাত এবং এই ত্রিভুজটি আবশ্যিকভাবেই একটি কেপলার ত্রিভুজ হবে।^[১]

A third, equivalent way of defining this triangle comes from a problem of maximizing the inradius of isosceles triangles. সমান দৈর্ঘ্যের দুটি নির্দিষ্ট বাহু নিয়ে এবং তৃতীয় বাহু বা ভূমির দৈর্ঘ্য স্বেচ্ছাধীন রেখে যতগুলো সমদ্বিবাহু ত্রিভুজ গঠন করা যাবে, সেগুলোর মধ্যে যে একটি সমদ্বিবাহু ত্রিভুজে সবচেয়ে বৃহত্তম দৈর্ঘ্যের অন্তর্ব্যাসার্ধটি পাওয়া যাবে, সেই সমদ্বিবাহু ত্রিভুজটি দুটি কেপলার ত্রিভুজের সমন্বয়ে গঠিত হবে, যেখানে এই কেপলার ত্রিভুজ দুটি হবে একে অপরের অনুলিপি এবং এরা হবে এদেরই ক্ষুদ্রতম বাহুর সাপেক্ষে পরস্পরের প্রতিফলিত ত্রিভুজ। এইকারণে, কেপলার ত্রিভুজকে সংজ্ঞায়িত করা যায় সেই সমকোণী ত্রিভুজরূপে, যে সমকোণী ত্রিভুজটি হবে, একই দৈর্ঘ্যের অতিভুজযুক্ত সকল সমকোণী ত্রিভুজের মধ্যে, এমন একটি সমকোণী ত্রিভুজ, যা গঠিত হবে এরই প্রতিফলিত রূপ নিয়ে তথা সর্ববৃহৎ অন্তর্ব্যাসার্ধযুক্ত সমদ্বিবাহু ত্রিভুজটি নিয়ে।^[১২] পক্ষান্তরে, কেপলার ত্রিভুজটি যখন এর লম্ব বাহু দুটির মধ্যে বৃহত্তর বাহুটির সাপেক্ষে প্রতিফলিত হয়, তখন একটি নির্দিষ্ট পরিসীমার জন্য এটি সম্ভাব্য সর্ববৃহৎ অর্ধবৃত্তটিকে ধারণ করে।^[১৩]

ধর্মাবলী

কক্সেটারের লোক্সোড্রোমিক অনুক্রম মেনে চলে এমন স্পর্শকীয় বৃত্তের ক্ষেত্রে প্রতি তিনটি ধারাবাহিক বৃত্তের কেন্দ্র এমন একটি কোণ গঠন করে যা কেপলার ত্রিভুজ কোণগুলোর একটির অনুরূপ।

যদি কেপলার ত্রিভুজের ক্ষুদ্রতম বাহুর দৈর্ঘ্য ${\displaystyle s}$ হয়, তাহলে এর অপর বাহু দুটির দৈর্ঘ্য হবে ${\displaystyle s{\sqrt {\varphi }}}$ এবং ${\displaystyle s\varphi }$। সমকোণী ত্রিভুজের ক্ষেত্রফল সমকোণ সংলগ্ন বাহু দুটির গুণফলের অর্ধেক। ফলে কেপলার ত্রিভুজটির ক্ষেত্রফল হবে ${\displaystyle {\tfrac {s^{2}}{2}}{\sqrt {\varphi }}}$। সমকোণ ব্যতীত অপর কোণ দুটির মধ্যে বৃহত্তর কোণটির কোসাইন হবে বৃহত্তর কোণ সংলগ্ন বাহু (সমকোণ সংলগ্ন বাহু দুটির মধ্যে ক্ষুদ্রতর বাহু ${\displaystyle s}$) এবং অতিভুজের (${\displaystyle s\varphi }$) অনুপাতের সমান। আবার, সমকোণ ব্যতীত অপর কোণ দুটির মধ্যে ক্ষুদ্রতর কোণটির সাইন হবে ক্ষুদ্রতর কোণের বিপরীত বাহু (অর্থাৎ এক্ষেত্রেও সমকোণ সংলগ্ন বাহু দুটির মধ্যে ক্ষুদ্রতর বাহু ${\displaystyle s}$) এবং অতিভুজের (${\displaystyle s\varphi }$) অনুপাতের সমান। অতএব, কেপলার ত্রিভুজটির সমকোণ ব্যতিত অপর কোণ দুটি হবে:^[১]

${\displaystyle \theta }$₂ ${\displaystyle =}$ ${\displaystyle \cos ^{-1}{\frac {1}{\varphi }}\approx 51.8273^{\circ }}$ এবং

${\displaystyle \theta }$₁ ${\displaystyle =}$ ${\displaystyle \sin ^{-1}{\frac {1}{\varphi }}\approx 38.1727^{\circ }}$

অবশ্য, প্রতিটি বাহুর মান জানা থাকায় অন্যান্য ত্রিকোণমিতিক অনুপাত ব্যবহার করেও এই কোণ দুটি বের করা সম্ভব।

স্পর্শকীয় বৃত্তে কক্সেটারের লোক্সোড্রোমিক অনুক্রমের ক্ষেত্রে ধারাবাহিক ত্রিভুজের ত্রয়ীগুলো তাদের কেন্দ্রে যে কোণটি উৎপন্ন করে, সেই কোণটি যে উপরোক্ত কেপলার কোণ দুটির মধ্যে বৃহত্তরটি, তা জার্জি কোচিক পর্যবেক্ষণ করেন।^[১৪]

তথ্যসূত্র

1. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; herz নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
2. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; fink নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
3. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; hoyrup নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
4. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; busard নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
5. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; fibonacci নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
6. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; bartlett নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
7. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; fischler নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
8. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; rossi নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
9. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; anglin নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
10. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; tout নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
11. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; markowsky নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
12. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; cow নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
13. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; detemple নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি
14. উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; kocik নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি

উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "anglin" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "bartlett" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "bruce" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "busard" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "cow" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "detemple" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "didom" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "fibonacci" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "fink" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "fischler" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "ghyka" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "herz" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "hoyrup" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "huffman" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "kocik" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "markowsky" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।
উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "rossi" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।

উদ্ধৃতি ত্রুটি: <references>-এ সংজ্ঞায়িত "tout" নামসহ <ref> ট্যাগ পূর্ববর্তী লেখায় ব্যবহৃত হয়নি।