স্পর্শক
এই নিবন্ধটি ইংরেজি থেকে আনাড়িভাবে অনুবাদ করা হয়েছে। এটি কোনও কম্পিউটার কর্তৃক অথবা দ্বিভাষিক দক্ষতাহীন কোনো অনুবাদক কর্তৃক অনূদিত হয়ে থাকতে পারে। |


জ্যামিতিতে, স্পর্শক রেখা (অথবা কেবল স্পর্শক) একটি সমতল থেকে বক্ররেখা একটি প্রদত্ত এ বিন্দু হয় সরল রেখা যে, "শুধু স্পর্শ" যে সময়ে বক্ররেখা। লেবনিজ এটি বক্ররেখা উপর অসীম বন্ধ পয়েন্ট একটি জোড়া মাধ্যমে লাইন হিসাবে সংজ্ঞায়িত । [1] আরো অবিকল, লাইনটি বিন্দু ( c , f ( c , c ( c , f ( c) এর মধ্য দিয়ে পাস করলে বক্ররেখা একটি বিন্দু x = c ( x ) এ একটি বক্ররেখা y = f ( x ) বক্ররেখা এবং ঢাল হয়েছে চ ' ( গ ) , যেখানে চ ' হয় ব্যুৎপন্ন এর চ । একই রকম সংজ্ঞা স্থান-বক্ররেখা এবং এন- ডাইমেনশনাল ইউক্লিডান স্পেসে কার্ভগুলিতে প্রযোজ্য ।
যেমনটি টানেন্ট লাইন এবং বক্ররেখা পূরণ করে, বিন্দুটিকে টেনেন্সি বলে অভিহিত করে , ত্যাঞ্চেন্ট লাইনটি বক্ররেখা হিসাবে "একই দিকের দিকে যাচ্ছে" এবং এভাবে বক্ররেখাটির সর্বোত্তম সোজা লাইনের আনুমানিকতা বিন্দু।
একইভাবে, প্রদত্ত বিন্দুতে পৃষ্ঠের ট্যানজেন্ট সমতল একটি সমতল যা সেই সময়ে পৃষ্ঠটিকে "শুধু স্পর্শ করে"। একটি টানেন্ট ধারণাটি ডিফারেনশিয়াল জ্যামিতিগুলির মধ্যে সবচেয়ে মৌলিক ধারণাগুলির মধ্যে একটি এবং ব্যাপকভাবে সাধারণকরণ করা হয়েছে; দেখতে ট্যানজেন্ট স্থান ।
"টাংজেন্ট" শব্দটি " টাচ" শব্দটি ল্যাটিন টঙ্গী থেকে এসেছে ।
ইতিহাস
[সম্পাদনা]ইউক্লিড স্পর্শক (বিভিন্ন রেফারেন্স তোলে ἐφαπτομένη ephaptoménē পুস্তক তৃতীয় মধ্যে একটি চেনাশোনাতে) উপাদানসমূহ (গ। 300 বিসি)। [২] এর মধ্যে অ্যাপোলোনিয়াস কাজ Conics (গ। 225 বিসি) তিনি হচ্ছে একটি স্পর্শক সংজ্ঞায়িত একটি লাইন যেমন যে অন্য কোন সরল রেখা পারে এটি এবং বক্ররেখা মধ্যে পড়ে । [3]
Archimedes (c। 287 - c। 212 BC) বক্ররেখা বরাবর সরানো একটি বিন্দু পথ বিবেচনা করে একটি আর্কিমিডিয়ান সর্পিল টানেন্ট পাওয়া । [3]
1630-এর দশকে Fermat বিশ্লেষণে টাঙ্গেন্ট এবং অন্যান্য সমস্যাগুলি গণনা করার জন্য পর্যাপ্ততার কৌশল বিকশিত করেন এবং প্যারাবোলাতে টাঙ্গেন্টগুলির গণনা করার জন্য এটি ব্যবহার করেন। Adeqality কৌশল মধ্যে পার্থক্য অনুরূপ এবং এবং একটি শক্তি দ্বারা বিভাজক । স্বাধীনভাবে Descartes পর্যবেক্ষণের উপর ভিত্তি করে আদর্শের তার পদ্ধতি ব্যবহার করে যে একটি বৃত্ত এর ব্যাসার্ধ বৃত্ত নিজেই স্বাভাবিক। [4]
এই পদ্ধতি 17 শতকের মধ্যে ডিফারেনশিয়াল ক্যালকুলাস বিকাশ নেতৃত্বে । অনেক মানুষ অবদান। রবার্ভাল একটি চলমান বিন্দু দ্বারা বর্ণিত একটি বক্ররেখা বিবেচনা করে টানেন্ট আঁকার একটি সাধারণ পদ্ধতি আবিষ্কার করেন, যার গতি অনেক সহজ গতির ফলাফল। [5] রেন-ফ্রাঙ্কো ডি স্লুস এবং জোহানেস হুড্ড টাঙ্গেন্ট খুঁজে বের করার জন্য বীজগণিত অ্যালগরিদম খুঁজে পেয়েছেন। [6] আরও বিকাশে জন ওয়ালিস এবং আইজাক ব্যারোর অন্তর্ভুক্ত ছিল , যার ফলে আইজাক নিউটন এবং গোটফ্রেড লিবনিজ তত্ত্বের সূচনা ঘটে ।
188২ সালের একটি টানেন্টের সংজ্ঞাটি "একটি সঠিক লাইন যা একটি বক্ররেখা স্পর্শ করে, কিন্তু যা উৎপাদিত হয় তা কাটা হয় না"। [7] এই পুরনো সংজ্ঞাটি কোন টানেন্ট থাকার পরিবর্তে বিন্দু বিন্দুকে বাধা দেয় । এটি বরখাস্ত করা হয়েছে এবং আধুনিক সংজ্ঞাগুলি লিবনিজের সমতুল্য, যারা বক্ররেখাটির সীমাহীন বন্ধকগুলির একটি জোড়ার মাধ্যমে লাইনের মতো লম্বা লাইন সংজ্ঞায়িত করেছেন ।
Tangent line to a curve
[সম্পাদনা]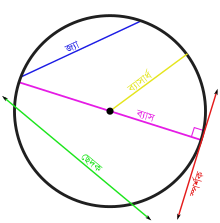
স্বতঃস্ফূর্ত ধারণা যে একটি টানেন্ট লাইনটি "ছোঁয়া" একটি বক্ররেখা সোজা বিন্দু ( সেকেন্ড লাইন গুলি) দুটি বিন্দু,এ এবং বি , যা ফাংশন বক্ররেখা থেকে থাকে, মাধ্যমে ক্রমানুসারে আরো স্পষ্ট করে তুলতে পারে । A এ টানেন্টটি সীমা যখন বি বি অনুমান করে বা A তে থাকে । ট্যানজেন্ট লাইনের অস্তিত্ব এবং অনন্যতা একটি নির্দিষ্ট ধরনের গাণিতিক মসৃণতা উপর নির্ভর করে, যা "ভিন্নতা" হিসাবে পরিচিত। উদাহরণস্বরূপ, যদি দুটি বৃত্তাকার arcs একটি তীক্ষ্ণ বিন্দু (একটি শূন্যস্থান) এ মিলিত হয় তবে শিরোনামের কোনও নির্দিষ্ট সংজ্ঞায়িত টানেন্ট নেই কারণ সেকেন্ড লাইনের অগ্রগতির সীমাটি সেই দিকের উপর নির্ভর করে যা "বিন্দু বি ""vertex পন্থা।
বেশিরভাগ পয়েন্টে, টানেন্টটি বক্ররেখাটি ছাড়াই বক্ররেখা স্পর্শ করে (যদিও এটি অব্যাহত থাকে তবে টেন্যান্টের বিন্দু থেকে দূরে অন্যান্য স্থানে বক্ররেখা অতিক্রম করে)। একটি বিন্দু যেখানে টানেন্ট (এই বিন্দুতে) বক্ররেখা অতিক্রম করে একটি বিন্দু বিন্দু বলা হয় । Circle s, parabola s, hyperbola s এবং ellipse গুলি এর কোনও বিন্দু বিন্দু নেই, তবে আরও জটিল কার্ভগুলি আছে, যেমন একটি ঘনক ফাংশনের গ্রাফের মতো , যার একটি ঠিক বিন্দু বিন্দু রয়েছে, বা একটি সিনাসয়েড, যার প্রতি দুইটি পরিবর্তনের পয়েন্ট রয়েছে প্রতিটি সময়ের এর সাইন ।
বিপরীতভাবে, এটি এমন হতে পারে যে বক্ররেখটি সোজা বিন্দুটির একপাশে একটি বিন্দুতে গিয়ে এটির একটি বিন্দুতে অবস্থিত, এবং তবুও এই সোজা লাইনটি টানেন্ট লাইন নয়। উদাহরণস্বরূপ, উদাহরণস্বরূপ, একটি ত্রিভুজের সারির মধ্য দিয়ে অতিক্রমকারী একটি লাইনের জন্য এবং অন্যথায় এটি ছেদ করে না-যেখানে উপরে বর্ণিত কারণগুলির জন্য টানেন্ট লাইন বিদ্যমান নেই। ইন উত্তল জ্যামিতি , এই ধরনের লাইন বলা হয় লাইন সমর্থনকারী ।

Analytical approach
[সম্পাদনা]টেকসেন্ট লাইনের সীমা লাইন সীমা লাইনের জ্যামিতিক ধারণা বিশ্লেষণাত্মক পদ্ধতিগুলির প্রেরণা হিসাবে কাজ করে যা স্পর্শকাতর টানেন্ট লাইনগুলি খুঁজে পেতে ব্যবহৃত হয়। 17 ই শতকের ক্যালকুলাসের বিকাশের দিকে পরিচালিত কেন্দ্রীয় প্রশ্নগুলির মধ্যে একটি গ্রাফে ট্যানজেন্ট লাইন বা ট্যানজেন্ট লাইন সমস্যাটি খোঁজার প্রশ্নটি ছিল। তার জ্যামিতি এর দ্বিতীয় বইয়ের মধ্যে , রেনি ডিসকার্টেস [8]একটি বক্ররেখা টানেন্ট তৈরির সমস্যা সম্পর্কে বলেন , "এবং আমি সাহস করে বলছি যে এই জ্যামিতি যা আমি জানি তা শুধুমাত্র সবচেয়ে দরকারী এবং সর্বাধিক সাধারণ সমস্যা নয়, এমনকি যে আমি কখনও জানতে চেয়েছিলেন।
Surfaces and higher-dimensional manifolds
[সম্পাদনা]স্পর্শক সমতল একটি থেকে পৃষ্ঠ একটি প্রদত্ত সময়ে পি রেখাচিত্র ক্ষেত্রে স্পর্শক রেখা একটি অনুরূপ ভাবে সংজ্ঞায়িত করা হয়। এটা ভাল একটি প্লেনে পৃষ্ঠের পড়তা হয় পি , আর প্লেন পৃষ্ঠ পাসে 3 স্বতন্ত্র পয়েন্ট মাধ্যমে ক্ষণস্থায়ী সীমিত অবস্থান যেমন প্রাপ্ত করা যাবে পি এই পয়েন্ট মিলিত যেমন পি । আরো সাধারণভাবে, একটি হল ট -dimensional স্পর্শক স্থান একটি প্রতিটি বিন্দুতে ট -dimensional নানাবিধ মধ্যে এন -dimensional ইউক্লিডিয় স্থান ।
আরও দেখুন
[সম্পাদনা]- নিউটন এর পদ্ধতি
- সাধারণ (জ্যামিতি)
- বৃত্তাকার অনুমান
- অনুভুত বক্ররেখা
- খাড়া
- উপস্পর্শক
- সাপোর্টিং লাইন
- টানেন্ট শঙ্কু
- টেনশিয়াল কোণ
- টেনশিয়াল উপাদান
- চেনাশোনা লম্বা লাইন
- বহুবচন (গণিত) # একটি বহুমূল্য ফাংশন কাছাকাছি একটি বহুবচন ফাংশন বহিষ্কার
- বীজগণিত বক্ররেখা # একটি বিন্দুতে টানেন্ট
তথ্যসূত্র
[সম্পাদনা]সূত্র
[সম্পাদনা]- J. Edwards (১৮৯২)। Differential Calculus। London: MacMillan and Co.। পৃষ্ঠা 143 ff.।
বহিঃসংযোগ
[সম্পাদনা]- Hazewinkel, Michiel, সম্পাদক (২০০১), "Tangent line", Encyclopedia of Mathematics, Springer Science+Business Media, আইএসবিএন 978-1-55608-010-4
- এরিক ডব্লিউ. ওয়াইস্টাইন সম্পাদিত ম্যাথওয়ার্ল্ড থেকে "Tangent Line"।
- Tangent to a circle With interactive animation
- Tangent and first derivative — An interactive simulation