Curtosi

Una distribució normal amb curtosi 3 (excés de curtosi 0)

En la teoria de la probabilitat i estadística, la curtosi, del grec: κυρτός, kirtós; (corba) convexa, és la mesura de la forma i el grau d'apuntament d'una distribució de probabilitat. En altres paraules, la curtosi mesura si la distribució és apuntada o és aplanada posant el focus en la forma de les cues laterals.^[1][2] Per una mateixa variància, com més alta sigui la curtosi d'una distribució significarà que una part més gran dels successos s'esdevenen prop la mitjana i a les cues (cues més gruixudes).

La curtosi és el quart moment estandarditzat, definit com:

${\textstyle \operatorname {Kurt} [X]=\operatorname {E} \left[\left({\frac {X-\mu }{\sigma }}\right)^{4}\right]}$

on μ és la mitjana i σ és la desviació estàndard.^[3]

Sovint es fa servir, en comptes de la curtosi, l'excés de curtosi, que és la diferència entre la curtosi d'una distribució i la de la distribució normal, que és 3.^[4][5] En alguns contextos s'anomena curtosi l'excés de curtosi, cosa que pot portar a situacions ambigües.

Un distribució amb coeficient de curtosi al voltant del de la normal (excés de curtosi proper a 0) s'anomena mesocúrtica; una amb un excés de curtosi negatiu indica un pic baix i unes cues amples que aviat s'aprimen als costats, s'anomena platicúrtica; una amb excés de curtosi positiu indica un apuntament del pic i unes cues llargues i gruixudes i s'anomena leptocúrtica.^[6]

En finances s'utilitza com a indicador de la volatilitat que presenta la cotització d'un valor financer.

Excés de curtosi en distribucions ben conegudes

Excés de curtosi en diferents distribucions amb mitjana 0 i variància 1

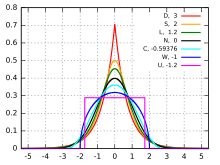
En aquest exemple, comparem diverses distribucions ben conegudes de diferents famílies paramètriques. Totes les densitats considerades aquí són unimodals i simètriques, amb una mitjana i l'asimetria de zero.

• D: distribució de Laplace, corba vermella, excés de curtosi = 3
• S: distribució secant hiperbòlica, corba taronja, excés de curtosi = 2
• L: distribució logística, corba verda, excés de curtosi = 1.2
• N: distribució normal, corba negra, excés de curtosi = 0
• C: distribució cosinus elevada, corba cian, excés de curtosi = -0.593762.
• W: distribució en semicercle de Wigner, corba blava, excés de curtosi = -1
• U: distribució uniforme, corba magenta, excés de curtosi = -1,2.

Referències

1. «kurtosis | statistics | Britannica» (en anglès). [Consulta: 25 gener 2022].
2. «Kurtosis Definition - What is Kurtosis?», 21-10-2011. Arxivat de l'original el 2011-10-21. [Consulta: 10 març 2022].
3. Aroca, Josep M. «Estadística. Notes de classe.». UPC.
4. Kurtosis. MathWorld (anglès)
5. Kurtosis Excess. MathWorld (anglès)
6. «Excess coefficient - Encyclopedia of Mathematics». [Consulta: 2 febrer 2022].