Distribució de Gumbel

Distribució de Gumbel

Funció de distribució de probabilitat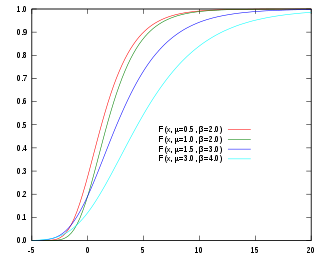
Tipus	Distribució generalitzada de valors extrems i distribució de probabilitat contínua
Epònim	Emil Julius Gumbel
Paràmetres	${\displaystyle \mu ,}$ location (real) ${\displaystyle \beta >0,}$ scale (real)

En teoria i estadística de probabilitats, la distribució de Gumbel (també coneguda com a distribució de valors extrems generalitzats de tipus I) s'utilitza per modelar la distribució del màxim (o del mínim) d'un nombre de mostres de diverses distribucions.^[1]

Aquesta distribució es pot utilitzar per representar la distribució del nivell màxim d'un riu en un any determinat si hi hagués una llista de valors màxims durant els darrers deu anys. És útil per predir la possibilitat que es produeixi un terratrèmol extrem, una inundació o un altre desastre natural. La possible aplicabilitat de la distribució de Gumbel per representar la distribució de màxims es relaciona amb la teoria del valor extrem, que indica que és probable que sigui útil si la distribució de les dades de la mostra subjacent és del tipus normal o exponencial. Aquest article utilitza la distribució de Gumbel per modelar la distribució del valor màxim. Per modelar el valor mínim, utilitzeu el negatiu dels valors originals. ^[2]

La distribució de Gumbel és un cas particular de la distribució de valors extrems generalitzada (també coneguda com a distribució de Fisher-Tippett). També es coneix com a distribució log-Weibull i distribució doble exponencial (un terme que de vegades s'utilitza alternativament per referir-se a la distribució de Laplace). Està relacionat amb la distribució de Gompertz: quan la seva densitat es reflecteix primer sobre l'origen i després es limita a la mitja línia positiva, s'obté una funció de Gompertz.

En la formulació de variables latents del model logit multinomial, comú en la teoria de l'elecció discreta, els errors de les variables latents segueixen una distribució de Gumbel. Això és útil perquè la diferència de dues variables aleatòries distribuïdes per Gumbel té una distribució logística.

La distribució de Gumbel porta el nom d'Emil Julius Gumbel (1891–1966), basat en els seus documents originals que descriuen la distribució.

Definicions ^[3]

La funció de distribució acumulada de la distribució de Gumbel és

${\displaystyle F(x;\mu ,\beta )=e^{-e^{-(x-\mu )/\beta }}.\,}$

Distribució estàndard de Gumbel

La distribució estàndard de Gumbel és el cas on ${\displaystyle \mu =0}$ i ${\displaystyle \beta =1}$ amb funció de distribució acumulada

${\displaystyle F(x)=e^{-e^{(-x)}}\,}$

i funció de densitat de probabilitat

${\displaystyle f(x)=e^{-(x+e^{-x})}.}$

En aquest cas el mode és 0, la mediana és ${\displaystyle -\ln(\ln(2))\approx 0.3665}$, la mitjana és ${\displaystyle \gamma \approx 0.5772}$ (la constant d'Euler-Mascheroni) i la desviació estàndard és ${\displaystyle \pi /{\sqrt {6}}\approx 1.2825.}$

Els cumulants, per n>1, estan donats per

${\displaystyle \kappa _{n}=(n-1)!\zeta (n).}$ ^[4]

Referències

1. «Gumbel Distribution | Real Statistics Using Excel» (en anglès). https://real-statistics.com.+[Consulta: 19 juny 2023].
2. «Gumbel Distribution - an overview | ScienceDirect Topics» (en anglès). https://www.sciencedirect.com.+[Consulta: 10 juny 2023].
3. Weisstein, Eric W. «Gumbel Distribution» (en anglès). https://mathworld.wolfram.com/.+[Consulta: 19 juny 2023].
4. «Gumbel Distribution: Definition, Examples» (en anglès). https://www.statisticshowto.com.+[Consulta: 19 juny 2023].