Distribució de Pareto generalitzada

Distribució de Pareto generalitzada

Funció de densitat de probabilitat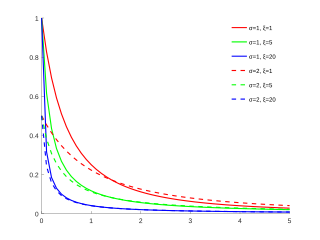
Funció de distribució de probabilitat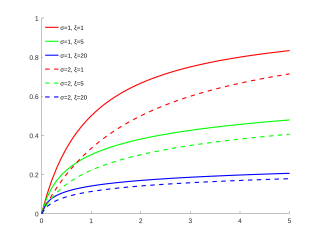
Tipus	distribució de probabilitat contínua
Paràmetres	${\displaystyle \mu \in (-\infty ,\infty )\,}$ ubicació (real) ${\displaystyle \sigma \in (0,\infty )\,}$ escala (real) ${\displaystyle \xi \in (-\infty ,\infty )\,}$ forma (real)
Suport	${\displaystyle x\geqslant \mu \,\;(\xi \geqslant 0)}$ ${\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi \,\;(\xi <0)}$
fdp	${\displaystyle {\frac {1}{\sigma }}(1+\xi z)^{-(1/\xi +1)}}$ on ${\displaystyle z={\frac {x-\mu }{\sigma }}}$
FD	${\displaystyle 1-(1+\xi z)^{-1/\xi }\,}$
Esperança matemàtica	${\displaystyle \mu +{\frac {\sigma }{1-\xi }}\,\;(\xi <1)}$
Mediana	${\displaystyle \mu +{\frac {\sigma (2^{\xi }-1)}{\xi }}}$
Moda	${\displaystyle \mu }$
Variància	${\displaystyle {\frac {\sigma ^{2}}{(1-\xi )^{2}(1-2\xi )}}\,\;(\xi <1/2)}$
Coeficient de simetria	${\displaystyle {\frac {2(1+\xi ){\sqrt {1-2\xi }}}{(1-3\xi )}}\,\;(\xi <1/3)}$
Curtosi	${\displaystyle {\frac {3(1-2\xi )(2\xi ^{2}+\xi +3)}{(1-3\xi )(1-4\xi )}}-3\,\;(\xi <1/4)}$
Entropia	${\displaystyle \log(\sigma )+\xi +1}$
FGM	${\displaystyle e^{\theta \mu }\,\sum _{j=0}^{\infty }\left[{\frac {(\theta \sigma )^{j}}{\prod _{k=0}^{j}(1-k\xi )}}\right],\;(k\xi <1)}$
FC	${\displaystyle e^{it\mu }\,\sum _{j=0}^{\infty }\left[{\frac {(it\sigma )^{j}}{\prod _{k=0}^{j}(1-k\xi )}}\right],\;(k\xi <1)}$

En estadística, la distribució de Pareto generalitzada (GPD) és una família de distribucions de probabilitat contínues. Sovint s'utilitza per modelar les cues d'una altra distribució. S'especifica per tres paràmetres: ubicació ${\displaystyle \mu }$, escala ${\displaystyle \sigma }$, i forma ${\displaystyle \xi }$.^[1][2] De vegades només s'especifica per l'escala i la forma^[3] i de vegades només pel seu paràmetre de forma. Algunes referències donen el paràmetre de forma com ${\displaystyle \kappa =-\xi \,}$.^[4]

Definició

La funció de distribució acumulada estàndard (cdf) de la GPD es defineix per ^[5]

${\displaystyle F_{\xi }(z)={\begin{cases}1-\left(1+\xi z\right)^{-1/\xi }&{\text{per a }}\xi \neq 0,\\1-e^{-z}&{\text{per a }}\xi =0.\end{cases}}}$

on hi ha el suport ${\displaystyle z\geq 0}$ per ${\displaystyle \xi \geq 0}$ i ${\displaystyle 0\leq z\leq -1/\xi }$ per ${\displaystyle \xi <0}$ . La funció de densitat de probabilitat corresponent (fdp) és

${\displaystyle f_{\xi }(z)={\begin{cases}(1+\xi z)^{-{\frac {\xi +1}{\xi }}}&{\text{per a }}\xi \neq 0,\\e^{-z}&{\text{per a }}\xi =0.\end{cases}}}$

Caracterització

La família de distribucions a escala de localització relacionada s'obté substituint l'argument z per ${\displaystyle {\frac {x-\mu }{\sigma }}}$ i ajustant el suport en conseqüència.

La funció de distribució acumulada de ${\displaystyle X\sim GPD(\mu ,\sigma ,\xi )}$ (${\displaystyle \mu \in \mathbb {R} }$, ${\displaystyle \sigma >0}$, i ${\displaystyle \xi \in \mathbb {R} }$) és

${\displaystyle F_{(\mu ,\sigma ,\xi )}(x)={\begin{cases}1-\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{-1/\xi }&{\text{per a }}\xi \neq 0,\\1-\exp \left(-{\frac {x-\mu }{\sigma }}\right)&{\text{per a }}\xi =0,\end{cases}}}$

on el suport de ${\displaystyle X}$ és ${\displaystyle x\geqslant \mu }$ Quan ${\displaystyle \xi \geqslant 0\,}$, i ${\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi }$ Quan ${\displaystyle \xi <0}$.

La funció de densitat de probabilitat (fdp) de ${\displaystyle X\sim GPD(\mu ,\sigma ,\xi )}$ és

${\displaystyle f_{(\mu ,\sigma ,\xi )}(x)={\frac {1}{\sigma }}\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{\left(-{\frac {1}{\xi }}-1\right)}}$

de nou, per ${\displaystyle x\geqslant \mu }$ Quan ${\displaystyle \xi \geqslant 0}$, i ${\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi }$ Quan ${\displaystyle \xi <0}$.

La fdp és una solució de l'equació diferencial següent:

${\displaystyle \left\{{\begin{array}{l}f'(x)(-\mu \xi +\sigma +\xi x)+(\xi +1)f(x)=0,\\f(0)={\frac {\left(1-{\frac {\mu \xi }{\sigma }}\right)^{-{\frac {1}{\xi }}-1}}{\sigma }}\end{array}}\right\}}$

Referències

1. Coles, Stuart. An Introduction to Statistical Modeling of Extreme Values (en anglès). Springer, 12-12-2001, p. 75. ISBN 9781852334598. 
2. Dargahi-Noubary, G. R. «. An Introduction to Statistical Modeling of Extreme Values». Mathematical Geology, 21, 8, 1989, pàg. 829–842. DOI: 10.1007/BF00894450.
3. Hosking, J. R. M.; Wallis, J. R. «"Parameter and Quantile Estimation for the Generalized Pareto Distribution"». Technometrics, 29, 3, 1987, pàg. 339–349. DOI: 10.2307/1269343. JSTOR: 1269343.
4. Davison, A. C.. «Modelling Excesses over High Thresholds, with an Application». A: de Oliveira. Statistical Extremes and Applications (en anglès). Kluwer, 30-9-1984, p. 462. ISBN 9789027718044. 
5. Embrechts, Paul. Modelling extremal events for insurance and finance (en anglès), 1-1-1997, p. 162. ISBN 9783540609315.