Factor atípic local

En la detecció d'anomalies, el factor local atípic ("outlier") (amb acrònim LOF) és un algorisme proposat per Markus M. Breunig, Hans-Peter Kriegel, Raymond T. Ng i Jörg Sander l'any 2000 per trobar punts de dades anòmals mitjançant la mesura de la desviació local d'un punt de dades donat. respecte als seus veïns.
LOF comparteix alguns conceptes amb DBSCAN i OPTICS, com ara els conceptes de "distància central" i "distància d'abast", que s'utilitzen per a l'estimació de la densitat local.[1]
Idea bàsica
[modifica]El factor atípic local es basa en un concepte de densitat local, on la localitat ve donada per k veïns més propers, la distància dels quals s'utilitza per estimar la densitat. En comparar la densitat local d'un objecte amb les densitats locals dels seus veïns, es poden identificar regions de densitat similar i punts que tenen una densitat substancialment menor que els seus veïns. Aquests es consideren atípics.
La densitat local s'estima per la distància típica a la qual es pot "arribar" a un punt des dels seus veïns. La definició de "distància d'abast" utilitzada a LOF és una mesura addicional per produir resultats més estables dins dels clústers. La "distància d'abast" utilitzada per LOF té alguns detalls subtils que sovint es troben incorrectes en fonts secundàries, per exemple, al llibre de text d'Ethem Alpaydin.[2]

Sigui k-distance(A) la distància de l'objecte A al k-è veí més proper. Tingueu en compte que el conjunt dels k veïns més propers inclou tots els objectes a aquesta distància, que en el cas d'un "empat" pot ser més de k objectes. Denotem el conjunt de k veïns més propers com Nk(A).
Aquesta distància s'utilitza per definir el que s'anomena distància d'accessibilitat.
En paraules, la distància d'accessibilitat d'un objecte A des de B és la distància real dels dos objectes, però almenys la k-distance de B. Els objectes que pertanyen als k veïns més propers de B (el "nucli" de B, vegeu l'anàlisi de clúster DBSCAN) es consideren igualment distants. La raó d'això és reduir les fluctuacions estadístiques entre tots els punts A propers a B, on augmentar el valor de k augmenta l'efecte de suavització. Tingueu en compte que aquesta no és una distància en la definició matemàtica, ja que no és simètrica. (Tot i que és un error comú [3] utilitzar sempre la k-distance(A), això produeix un mètode lleugerament diferent, conegut com Simplified-LOF [3])
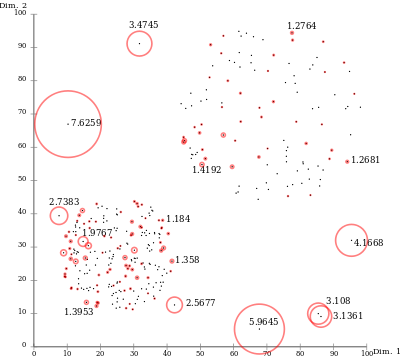
Advantages
[modifica]A causa de l'enfocament local, LOF és capaç d'identificar valors atípics en un conjunt de dades que no serien valors atípics en una altra àrea del conjunt de dades. Per exemple, un punt a una distància "petita" a un cúmul molt dens és un valor atípic, mentre que un punt dins d'un cúmul escàs pot mostrar distàncies similars als seus veïns. The LOF family of methods can be easily generalized and then applied to various other problems, such as detecting outliers in geographic data, video streams or authorship networks.[4]
La família de mètodes LOF es pot generalitzar fàcilment i després aplicar-se a diversos altres problemes, com ara la detecció de valors atípics en dades geogràfiques, fluxos de vídeo o xarxes d'autoria.[4]
Desadvantages
[modifica]Els valors resultants són valors quocients i difícils d'interpretar. Un valor d'1 o fins i tot menys indica un inlier clar, però no hi ha una regla clara per quan un punt sigui un valor atípic. En un conjunt de dades, un valor d'1,1 ja pot ser un valor atípic, en un altre conjunt de dades i parametrització (amb fortes fluctuacions locals) un valor de 2 encara podria ser un valor atípic. Aquestes diferències també es poden produir dins d'un conjunt de dades a causa de la localitat del mètode.
Referències
[modifica]- ↑ Breunig, M. M.. «OPTICS-OF: Identifying Local Outliers». A: Principles of Data Mining and Knowledge Discovery (en anglès). 1704, 1999, p. 262–270 (Lecture Notes in Computer Science). DOI 10.1007/978-3-540-48247-5_28. ISBN 978-3-540-66490-1.
- ↑ Alpaydin, Ethem. Introduction to machine learning (en anglès). Fourth, 2020. ISBN 978-0-262-04379-3. OCLC 1108782604.
- ↑ 3,0 3,1 Schubert, E.; Zimek, A.; Kriegel, H. -P. Data Mining and Knowledge Discovery, 28, 2012, pàg. 190–237. DOI: 10.1007/s10618-012-0300-z.
- ↑ 4,0 4,1 Schubert, E.; Zimek, A.; Kriegel, H. -P. Data Mining and Knowledge Discovery, 28, 2012, pàg. 190–237. DOI: 10.1007/s10618-012-0300-z.