Mapa autoorganitzat
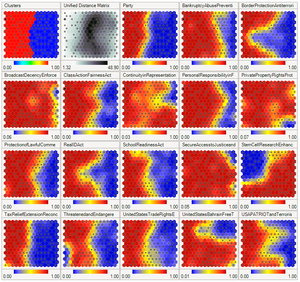
Un mapa autoorganitzat (SOM) o un mapa de característiques autoorganitzats (SOFM) és una tècnica d'aprenentatge automàtic no supervisat que s'utilitza per produir una representació de dimensions baixes (normalment bidimensional) d'un conjunt de dades de dimensions superiors mentre es preserva l'estructura topològica del dades. Per exemple, un conjunt de dades amb variables mesurades en les observacions es podrien representar com a grups d'observacions amb valors similars per a les variables. Aleshores, aquests cúmuls es podrien visualitzar com un "mapa" bidimensional de manera que les observacions en cúmuls proximals tinguin valors més similars que les observacions en cúmuls distals. Això pot fer que les dades d'alta dimensió siguin més fàcils de visualitzar i analitzar.
Un SOM és un tipus de xarxa neuronal artificial però s'entrena utilitzant l'aprenentatge competitiu en lloc de l'aprenentatge de correcció d'errors (p. ex., retropropagació amb descens de gradient) utilitzat per altres xarxes neuronals artificials. El SOM va ser introduït pel professor finlandès Teuvo Kohonen a la dècada de 1980 i, per tant, de vegades s'anomena mapa de Kohonen o xarxa de Kohonen.[1][2] El mapa o xarxa de Kohonen és una abstracció computacionalment convenient que es basa en models biològics de sistemes neuronals de la dècada de 1970 [3] i models de morfogènesi que es remunten a Alan Turing a la dècada de 1950.[4] Els SOM creen representacions internes que recorden l'homuncle cortical,[5] una representació distorsionada del cos humà, basada en un "mapa" neurològic de les àrees i proporcions del cervell humà dedicades a processar les funcions sensorials, per a diferents parts del cos.
Visió general
[modifica]Els mapes autoorganitzats, com la majoria de xarxes neuronals artificials, funcionen de dues maneres: entrenament i mapeig. En primer lloc, l'entrenament utilitza un conjunt de dades d'entrada (l'"espai d'entrada") per generar una representació de dimensions inferiors de les dades d'entrada (l'"espai del mapa"). En segon lloc, el mapping classifica les dades d'entrada addicionals mitjançant el mapa generat.
En la majoria dels casos, l'objectiu de l'entrenament és representar un espai d'entrada amb p dimensions com un espai de mapa amb dues dimensions. Concretament, es diu que un espai d'entrada amb p variables té p dimensions. Un espai de mapa està format per components anomenats "nodes" o "neurones", que estan disposats com una quadrícula hexagonal o rectangular amb dues dimensions.[6] El nombre de nodes i la seva disposició s'especifiquen prèviament en funció dels objectius més grans de l'anàlisi i exploració de les dades.
Cada node de l'espai del mapa està associat amb un vector "pes", que és la posició del node a l'espai d'entrada. Mentre que els nodes de l'espai del mapa es mantenen fixos, l'entrenament consisteix a moure vectors de pes cap a les dades d'entrada (reduint una mètrica de distància com la distància euclidiana) sense fer malbé la topologia induïda des de l'espai del mapa. Després de l'entrenament, el mapa es pot utilitzar per classificar observacions addicionals per a l'espai d'entrada trobant el node amb el vector de pes més proper (mètrica de distància més petita) al vector d'espai d'entrada.

Algorisme d'aprenentatge
[modifica]L'objectiu de l'aprenentatge en el mapa d'autoorganització és fer que diferents parts de la xarxa responguin de manera similar a determinats patrons d'entrada. Això està motivat en part per com es gestiona la informació visual, auditiva o sensorial en parts separades de l'escorça cerebral del cervell humà.
Els pesos de les neurones s'inicien a petits valors aleatoris o es mostren uniformement des del subespai abastat pels dos vectors propis de components principals més grans. Amb aquesta darrera alternativa, l'aprenentatge és molt més ràpid perquè els pesos inicials ja donen una bona aproximació dels pesos SOM.[7]
La xarxa ha de ser alimentada amb un gran nombre de vectors d'exemple que representin, el més proper possible, els tipus de vectors esperats durant el mapeig. Els exemples solen administrar-se diverses vegades com a iteracions.
La formació utilitza l'aprenentatge competitiu. Quan un exemple d'entrenament s'alimenta a la xarxa, es calcula la seva distància euclidiana a tots els vectors de pes. La neurona el vector de pes de la qual és més semblant a l'entrada s'anomena la millor unitat de concordança (BMU). Els pesos de la BMU i les neurones properes a la quadrícula SOM s'ajusten cap al vector d'entrada. La magnitud del canvi disminueix amb el temps i amb la distància de la xarxa des de la BMU. La fórmula d'actualització per a una neurona v amb el vector de pes W v (s) és
on s és l'índex de pas, t és un índex de la mostra d'entrenament, u és l'índex de la BMU per al vector d'entrada D(t), α(s) és un coeficient d'aprenentatge decreixent monòtonament; θ(u, v, s) és la funció de proximitat que dona la distància entre la neurona u i la neurona v al pas s.[8] Depenent de les implementacions, t pot escanejar el conjunt de dades d'entrenament sistemàticament (t és 0, 1, 2. . . T -1 i, a continuació, repetiu, sent T la mida de la mostra d'entrenament), extreu-vos aleatòriament del conjunt de dades (mostreig d'arrencada) o implementeu algun altre mètode de mostreig (com ara jackknifing).
Referències
[modifica]- ↑ Kohonen, Teuvo; Honkela, Timo Scholarpedia, 2, 1, 2007, pàg. 1568. Bibcode: 2007SchpJ...2.1568K. DOI: 10.4249/scholarpedia.1568 [Consulta: lliure].
- ↑ Kohonen, Teuvo Biological Cybernetics, 43, 1982, pàg. 59–69. DOI: 10.1007/bf00337288.
- ↑ Von der Malsburg, C Kybernetik, 14, 2, 1973, pàg. 85–100. DOI: 10.1007/bf00288907. PMID: 4786750.
- ↑ Turing, Alan Phil. Trans. R. Soc., 237, 641, 1952, pàg. 37–72. Bibcode: 1952RSPTB.237...37T. DOI: 10.1098/rstb.1952.0012 [Consulta: free].
- ↑ «Homunculus | Meaning & Definition in UK English | Lexico.com» (en anglès). Lexico Dictionaries | English. Arxivat de l'original el 18 maig 2021. [Consulta: 6 febrer 2022].
- ↑ Jaakko Hollmen. «Self-Organizing Map (SOM)» (en anglès). Aalto University, 09-03-1996.
- ↑ Kohonen, Teuvo. «Intro to SOM» (en anglès). SOM Toolbox. [Consulta: 18 juny 2006].
- ↑ Kohonen, Teuvo; Honkela, Timo Scholarpedia, 2, 1, 2011, pàg. 1568. Bibcode: 2007SchpJ...2.1568K. DOI: 10.4249/scholarpedia.1568 [Consulta: free].


