Massa mínima
Dreta: En aquest cas, cap moviment de l'estrella es troba al llarg de la línia de visió de l'espectador i el mètode d'espectroscòpia Doppler no detectarà el planeta en absolut.
En astronomia, massa mínima és el càlcul del límit inferior de la massa dels objectes observats, com ara planetes, estrelles, sistemes binaris,[1] nebuloses,[2] i forats negres.
La massa mínima és una estadística àmpliament citada per als planetes extrasolars detectats pel mètode de velocitat radial o espectroscòpia Doppler, i es determina mitjançant la funció de massa binària. Aquest mètode revela planetes mesurant els canvis en el moviment de les estrelles en la línia de visió, de manera que les inclinacions orbitals reals i les masses reals dels planetes són generalment desconegudes.[3] Això és el resultat del pecat i la degeneració.
Si es pot determinar la inclinació i, la massa real es pot obtenir a partir de la massa mínima calculada utilitzant la relació següent:
(On i indica l'angle d'inclinació).
Planetes extrasolars
[modifica]Orientació del trànsit a la Terra
[modifica]
La majoria de les estrelles no tindran els seus planetes alineats i orientats de manera que s'eclipsin sobre el centre de l'estrella i donin a l'espectador a la Terra un trànsit perfecte. És per aquest motiu que quan sovint només som capaços d'extrapolar una massa mínima en veure la vacil·lació d'una estrella perquè no coneixem la inclinació i, per tant, només podem calcular la part que estira l'estrella en el pla de l'esfera celeste.
Per als cossos orbitants en sistemes planetaris extrasolars, una inclinació de 0° o 180° correspon a una òrbita de cara (que no es pot observar amb la velocitat radial), mentre que una inclinació de 90° correspon a una òrbita de vora. òrbita (per a la qual la massa real és igual a la massa mínima).[4]
Els planetes amb òrbites molt inclinades a la línia de visió des de la Terra produeixen oscil·lacions visibles més petites i, per tant, són més difícils de detectar. Un dels avantatges del mètode de la velocitat radial és que l'excentricitat de l'òrbita del planeta es pot mesurar directament. Un dels principals desavantatges del mètode de velocitat radial és que només pot estimar la massa mínima d'un planeta (). Això s'anomena Sin i degeneració. La distribució posterior de l'angle d'inclinació i depèn de la distribució de massa real dels planetes.[5]
Mètode de velocitat radial
[modifica]Tanmateix, quan hi ha diversos planetes al sistema que orbiten relativament a prop els uns dels altres i tenen massa suficient, l'anàlisi d'estabilitat orbital permet limitar la massa màxima d'aquests planetes. El mètode de velocitat radial es pot utilitzar per confirmar les troballes fetes pel mètode de trànsit. Quan s'utilitzen tots dos mètodes en combinació, es pot estimar la massa real del planeta..
Encara que la velocitat radial de l'estrella només dona la massa mínima d'un planeta, si es poden distingir les línies espectrals del planeta de les línies espectrals de l'estrella, es pot trobar la velocitat radial del mateix planeta, i això dona la inclinació de la l'òrbita del planeta. Això permet mesurar la massa real del planeta. Això també descarta falsos positius i també proporciona dades sobre la composició del planeta. El problema principal és que aquesta detecció només és possible si el planeta orbita al voltant d'una estrella relativament brillant i si el planeta reflecteix o emet molta llum.[6]
El terme massa veritable és sinònim del terme massa, però s'empra en astronomia per diferenciar la massa mesurada d'un planeta de la massa mínima que s'obté normalment a partir de tècniques de velocitat radial.[7] Els mètodes utilitzats per determinar la massa real d'un planeta inclouen mesurar la distància i el període d'un dels seus satèl·lits,[8] tècniques avançades d'astrometria que utilitzen els moviments d'altres planetes del mateix sistema estel·lar,[7] combinant tècniques de velocitat radial amb observacions de trànsit (que indiquen inclinacions orbitals molt baixes),[9] i combinant tècniques de velocitat radial amb mesures de paral·laxi estel·lar (que també determinen les inclinacions orbitals).[10]
Ús de la funció sinus
[modifica]
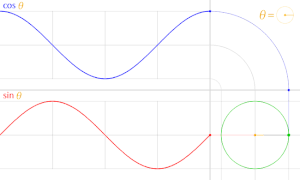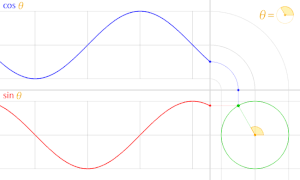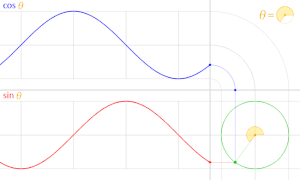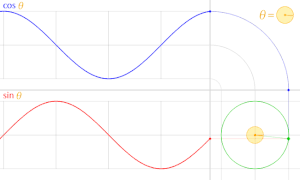
En trigonometria, un cercle unitari és el cercle de radi un centrat a l'origen (0, 0) en el sistema de coordenades cartesianes.
Deixeu que una línia passant per l'origen, fent un angle de θ amb la meitat positiva de l'eix x, talli el cercle unitari. Les coordenades x- i y-d'aquest punt d'intersecció són iguals a cos(θ) i sin(θ) , respectivament. La distància del punt des de l'origen és sempre 1.
Estrelles
[modifica]Amb una massa de només 93 vegades la de Júpiter (MJ), o .09 M☉, AB Doradus C, un company d'AB Doradus A, és l'estrella més petita coneguda que pateix fusió nuclear al seu nucli.[11] Per a les estrelles amb una metal·licitat similar a la del Sol, s'estima que la massa mínima teòrica que pot tenir l'estrella, i encara experimentar una fusió al nucli, és d'aproximadament de 75 MJ.[12][13] Quan la metal·licitat és molt baixa, però, un estudi recent de les estrelles més febles va trobar que la mida mínima de l'estrella sembla ser al voltant del 8,3% de la massa solar, o aproximadament de 87 MJ.[13][14] Els cossos més petits s'anomenen nanes marrons, que ocupen una zona grisa poc definida entre les estrelles i les gegants gasoses.
Referències
[modifica]- ↑ Kuchner, Marc J. «A Minimum-Mass Extrasolar Nebula» (en anglès). The Astrophysical Journal. The American Astronomical Society, 612, 2, setembre 2004, pàg. 1147–1151. arXiv: astro-ph/0405536. Bibcode: 2004ApJ...612.1147K. DOI: 10.1086/422577.
- ↑ Arbutina, B. «The minimum mass ratio of W UMa-type binary systems» (en anglès). Monthly Notices of the Royal Astronomical Society, 377, 4, juny 2007, pàg. 1635–1637. Bibcode: 2007MNRAS.377.1635A. DOI: 10.1111/j.1365-2966.2007.11723.x.
- ↑ Rothery, David A.; Gilmour, Iain; Sephton, Mark A. An Introduction to Astrobiology (en anglès), març 2018, p. 234–236. ISBN 9781108430838.
- ↑ Fleisch, Daniel; Kregenow, Julia. A Student's Guide to the Mathematics of Astronomy (en anglès), 29 d'agost de 2013, p. 97–101. ISBN 9781107610217.
- ↑ Stevens, Daniel J.; Gaudi, B. Scott «A Posteriori Transit Probabilities» (en anglès). Publications of the Astronomical Society of the Pacific, 125, 930, 2013, pàg. 933–950. arXiv: 1305.1298. Bibcode: 2013PASP..125..933S. DOI: 10.1086/672572.
- ↑ Rodler, Florian; Lopez-Morales, Mercedes; Ribas, Ignasi «Weighing the Non-Transiting Hot Jupiter Tau BOO b» (en anglès). The Astrophysical Journal, 753, 1, 2012, pàg. L25. arXiv: 1206.6197. Bibcode: 2012ApJ...753L..25R. DOI: 10.1088/2041-8205/753/1/L25.
- ↑ 7,0 7,1 «McDonald Observatory astronomers discover Neptune-sized planet with Hobby-Eberly Telescope» (en anglès). Universitat de Texas a Austin, 31-08-2004. Arxivat de l'original el 13 de febrer de 2007. [Consulta: 13 juliol 2023].
- ↑ Brown, Michael E.; Schaller, Emily L. «The Mass of Dwarf Planet Eris». Science, 316, 5831, 15-06-2007, pàg. 1585. Bibcode: 2007Sci...316.1585B. DOI: 10.1126/science.1139415. PMID: 17569855.
- ↑ «How do we know the density of some extrasolar planets?» (en anglès). Curious About Astronomy?. Arxivat de l'original el 12 d'octubre de 2007. [Consulta: 13 juliol 2023].
- ↑ Han, Inwoo; Black, David C.; Gatewood, George «Preliminary Astrometric Masses for Proposed Extrasolar Planetary Companions» (en anglès). The Astrophysical Journal Letters, 548, 1, 12-02-2001, pàg. L57–L60. Bibcode: 2001ApJ...548L..57H. DOI: 10.1086/318927.
- ↑ «Weighing the Smallest Stars» (en anglès). European Southern Observatory Press Release. ESO, 01-01-2005, pàg. 2. Bibcode: 2005eso..pres....2. [Consulta: 13 juliol 2023].
- ↑ Boss, Alan «Are They Planets or What?» (en anglès). Carnegie Institution of Washington, 03-04-2001 [Consulta: 13 juliol 2023].
- ↑ 13,0 13,1 Shiga, David «Mass cut-off between stars and brown dwarfs revealed» (en anglès). New Scientist, 17-08-2006. Arxivat de l'original el 14 de novembre de 2006 [Consulta: 13 juliol 2023].
- ↑ «Hubble glimpses faintest stars» (en anglès). BBC, 18-08-2006 [Consulta: 13 juliol 2023].




