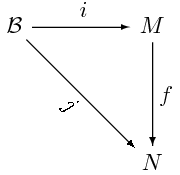
Si a l'estructura d'espai vectorial hom substitueix el cos d'escalars per un anell, l'estructura obtinguda és la de mòdul. Naturalment, moltes de les propietats es perden en aquest canvi i l'estructura de mòdul lliure és la que més s'acosta a la d'espai vectorial. Resulta significatiu que, per definir-la, només calgui reproduir el fet que qualsevol homomorfisme d'espais vectorials queda determinat quan se'n coneixen les imatges dels elements d'una base.
Posem això en una notació adequada: si  i
i  són espais vectorials i
són espais vectorials i  és una base de
és una base de  , una aplicació
, una aplicació  informa quant a quina és la imatge de cada element de la base
informa quant a quina és la imatge de cada element de la base  de
de  i només d'això. Però aleshores, ha quedat perfectament determinat un homomorfisme
i només d'això. Però aleshores, ha quedat perfectament determinat un homomorfisme  de manera que si
de manera que si  és la injecció natural, el següent diagrama
és la injecció natural, el següent diagrama
és commutatiu. La definició del  -mòdul lliure sobre el conjunt de generadors explota aquest fet exhaustivament.
-mòdul lliure sobre el conjunt de generadors explota aquest fet exhaustivament.
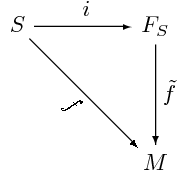
Siguin  un anell commutatiu amb unitat i
un anell commutatiu amb unitat i  un conjunt. El
un conjunt. El  -mòdul lliure sobre el conjunt de generadors
-mòdul lliure sobre el conjunt de generadors  , denotat
, denotat  , és l'únic
, és l'únic  -mòdul proveït d'una aplicació
-mòdul proveït d'una aplicació  que compleix que, per qualsevol altre
que compleix que, per qualsevol altre  -mòdul
-mòdul  i qualsevol aplicació
i qualsevol aplicació  , hi ha un únic homomorfisme de mòduls,
, hi ha un únic homomorfisme de mòduls,  que fa que el següent diagrama
que fa que el següent diagrama
sigui commutatiu, això és, que  .
.
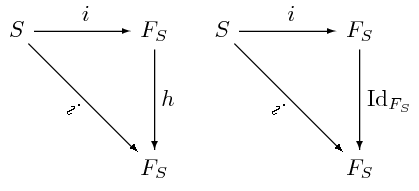
Comencem per veure que, si  és un homomorfisme de mòduls que fa
és un homomorfisme de mòduls que fa  , aleshores
, aleshores  és la identitat. En efecte, en el diagrama de la dreta
és la identitat. En efecte, en el diagrama de la dreta
la commutativitat és òbvia i la unicitat establerta per la definició per a  del diagrama de l'esquerra obliga que
del diagrama de l'esquerra obliga que  .
.
Sigui ara  un altre mòdul lliure sobre el conjunt de generadors
un altre mòdul lliure sobre el conjunt de generadors  . Tenim els següents diagrames commutatius:
. Tenim els següents diagrames commutatius:
o sigui,

|
que, per substitució, dona

|
Ara bé, segons l'observació inicial, ha de ser

|
i, per tant,  i
i  són inverses l'una de l'altra i, en conseqüència, els dos mòduls lliures,
són inverses l'una de l'altra i, en conseqüència, els dos mòduls lliures,  i
i  són isomorfs. A més, per la condició d'unicitat, no hi ha cap altre isomorfisme que respecti les aplicacions
són isomorfs. A més, per la condició d'unicitat, no hi ha cap altre isomorfisme que respecti les aplicacions  i
i  : tenim, doncs, que aquest isomorfisme és únic.
: tenim, doncs, que aquest isomorfisme és únic.
El conjunt  genera el mòdul lliure
genera el mòdul lliure  , això és, qualsevol submòdul
, això és, qualsevol submòdul  que contingui
que contingui  és exactament igual a
és exactament igual a  . A més, el conjunt
. A més, el conjunt  és lliure, és a dir, els seus elements són linealment independents.
és lliure, és a dir, els seus elements són linealment independents.
Per veure-ho, considerem les aplicacions
|

|
i la projecció canònica  . Aleshores, els dos diagrames
. Aleshores, els dos diagrames
són òbviament commutatius i, de la unicitat, en resulta  , és a dir, que la projecció canònica és nul·la i, per tant, que
, és a dir, que la projecció canònica és nul·la i, per tant, que  .
.
La independència lineal dels elements de  es pot establir així: per a un element determinat
es pot establir així: per a un element determinat  , considerem l'aplicació
, considerem l'aplicació
|

|
|

|
En considerar l'anell  com a
com a  -mòdul, hi ha el morfisme induït al mòdul lliure
-mòdul, hi ha el morfisme induït al mòdul lliure  que fa
que fa  . Prenem ara qualsevol suma finita
. Prenem ara qualsevol suma finita
|

|
Tenim:
|

|
i, com que això s'esdevé per qualsevol índex  , resulta que
, resulta que  i la independència lineal queda demostrada. Aleshores,
i la independència lineal queda demostrada. Aleshores,  és una base del mòdul lliure
és una base del mòdul lliure  .
.
Inversament, tot  -mòdul
-mòdul  proveït d'una base
proveït d'una base  , és a dir, d'un conjunt de generadors lliure, és un mòdul lliure sobre aquest conjunt de generadors. En efecte, primer definim l'aplicació
, és a dir, d'un conjunt de generadors lliure, és un mòdul lliure sobre aquest conjunt de generadors. En efecte, primer definim l'aplicació
|

|
|

|
i ara, si  és un altre
és un altre  -mòdul i
-mòdul i  és una aplicació qualsevol de
és una aplicació qualsevol de  a
a  , l'aplicació
, l'aplicació
|

|
|

|
és, trivialment, un homomorfisme de  a
a  i el següent diagrama
i el següent diagrama
és commutatiu.
En particular, si l'anell  és un cos, aleshores
és un cos, aleshores  és un espai vectorial sobre
és un espai vectorial sobre  i, com a tal, té almenys una base. En conseqüència, tots els espais vectorials són lliures sobre cadascuna de les seves bases.
i, com a tal, té almenys una base. En conseqüència, tots els espais vectorials són lliures sobre cadascuna de les seves bases.
En realitat, allò que descriu aquest apartat és que un homomorfisme entre  -mòduls, el domini del qual és lliure, queda determinat per les imatges dels elements d'una base qualsevol del domini.
-mòduls, el domini del qual és lliure, queda determinat per les imatges dels elements d'una base qualsevol del domini.
A-mòduls lliures de generació finita
[modifica]Si  és un conjunt finit, el
és un conjunt finit, el  -mòdul lliure
-mòdul lliure  es diu de generació finita o finitament generat. Hom pot considerar, sense inconvenient, substituir el conjunt
es diu de generació finita o finitament generat. Hom pot considerar, sense inconvenient, substituir el conjunt  , de
, de  elements, pel conjunt finit
elements, pel conjunt finit
|

|
Aleshores,  se sol denotar per
se sol denotar per  , tot expressant que el mòdul lliure sobre el conjunt
, tot expressant que el mòdul lliure sobre el conjunt  no és altra cosa que el producte directe de
no és altra cosa que el producte directe de  exemplars de l'anell
exemplars de l'anell  , els elements en són
, els elements en són  -tuples d'elements de l'anell, amb la suma de
-tuples d'elements de l'anell, amb la suma de  -tuples i la multiplicació per elements de l'anell en la forma usual.
-tuples i la multiplicació per elements de l'anell en la forma usual.
Si  és l'
és l' -mòdul lliure amb generadors
-mòdul lliure amb generadors  , i
, i  és un altre mòdul lliure, una aplicació
és un altre mòdul lliure, una aplicació  determina un únic homomorfisme
determina un únic homomorfisme  entre ambdós mòduls. La descripció de l'aplicació
entre ambdós mòduls. La descripció de l'aplicació  se sol fer mitjançant una matriu de
se sol fer mitjançant una matriu de  files i
files i  columnes,
columnes,
|

|
d'elements de l'anell  de manera que la columna
de manera que la columna  conté l'expressió de
conté l'expressió de  en alguna base d'aquest últim mòdul. La matriu, doncs, determina l'homomorfime
en alguna base d'aquest últim mòdul. La matriu, doncs, determina l'homomorfime  de manera unívoca.
de manera unívoca.
En conseqüència, l'àlgebra de les matrius  d'elements de l'anell
d'elements de l'anell  és isomorfa a l'àlgebra dels homomorfismes de
és isomorfa a l'àlgebra dels homomorfismes de  a
a  .
.
Construirem ara efectivament el  -mòdul lliure sobre un conjunt de generadors
-mòdul lliure sobre un conjunt de generadors  . El conjunt
. El conjunt  és el conjunt de totes les funcions
és el conjunt de totes les funcions  que prenen el valor
que prenen el valor  excepte en un nombre finit d'elements de
excepte en un nombre finit d'elements de  . Clarament, les operacions
. Clarament, les operacions
|

|
fan de  un
un  -mòdul.
-mòdul.
Però l'aplicació  definida per
definida per
|

|
fa de  el
el  -mòdul lliure sobre un conjunt de generadors
-mòdul lliure sobre un conjunt de generadors  . En efecte, sigui
. En efecte, sigui  una aplicació del conjunt
una aplicació del conjunt  sobre un cert
sobre un cert  -mòdul
-mòdul  . L'aplicació
. L'aplicació
|

|
|

|
és un morfisme d' -mòduls perquè
-mòduls perquè
|

|
|

|
i, si  és un altre morfisme que fa
és un altre morfisme que fa  , aleshores, per a
, aleshores, per a  , com que
, com que  genera
genera  ,
,
|

|
i
|

|
i, per tant,  . En conseqüència, el
. En conseqüència, el  -mòdul
-mòdul  així construït és el
així construït és el  -mòdul lliure generat pel conjunt
-mòdul lliure generat pel conjunt  .
.
|
|---|
| Espais dimensionals | | |
|---|
| Altres dimensions | |
|---|
| Polítops i formes | |
|---|
| Dimensions per nombre | |
|---|
|