Processament digital d'imatges
El processament digital d'imatges és l'ús d'un computador digital per processar imatges mitjançant un algorisme. Al ser una subcategoria del processament digital de senyals, el processament digital d'imatges té molts avantatges en comparació amb el processament analògic d'imatges. Això permet tenir un rang més ample d'algorismes que poden ser aplicats a les dades d'entrada i es poden evitar problemes com la creació de soroll i distorsió durant aquest processament digital. Des que les imatges poden ser definides en dos dimensions (encara que poden ser més), el processament digital d'imatges pot ser modelats en la forma de sistemes multidimensionals. La generació i desenvolupament del processament digital d'imatges estan afectats principalment per tres factors: el primer, el desenvolupament de computadors; el segon, el desenvolupament de les matemàtiques (especialment en la creació i millora de la teoria de matemàtica discreta); i el tercer, la demanda per un ampli rang d'aplicacions en la ciència medioambiental, de l'agricultura, militar, industrial i mèdica ha augmentat.
Transformació digital d'imatges
[modifica]La transformació digital d'imatges permet millorar la qualitat o resaltar detalls que no es veuen a simple vista amb claredat. Quan es transforma una imatge, s'obté una imatge B a partir d'una imatge A, encara que poden ser més d'una imatge, i la forma que es modifica A per convertir-se en B determina el tipus de transformació.[1]
Transformacions puntuals
[modifica]En el cas de les transformacions puntuals, cada píxel de la imatge transformada s'obtenen a partir del píxel de la imatge original amb les mateixes coordenades, sense tenir en compte els píxels veïns d'aquest. És a dir, aquestes transformacions es realitzen punt a punt de la imatge.
Existeixen diversos tipus de transformacions puntuals:
- Transformacions puntuals simples
- Umbralització
- LUT
- Transformacions lineals
- Imatge negativa
- Maximització del contrast
- Transformacions no lineals
- Logaritme
- Exponencial
- Operacions lògiques
- Equalització
Transformacions puntuals simples
[modifica]Aquest tipus de transformacions treballen només amb una imatge original, on cada píxel es considera un element individual, sense mirar els veïns. S'aplica una funció que depèn exclusivament del valor del píxel.[2]
La transformació puntual transforma la imatge en funció del nivell de grisos dels seus píxels.
Umbralització
[modifica]La umbralització, també conegut com binarització o threshold, consisteix en convertir la imatge digital en una imatge en blanc i negre, de tal manera que es preservin les propietats escencials de la imatge.
Existeixen dos tipus de umbralitzacions:
- Umbral simple. Els punts amb un nivell d'intensitat major o igual a un cert umbral t reben el nivell màxim i la resta, el nivell mínim.

Umbral simple 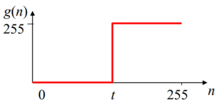
Representació umbral simple - Umbral doble. S'escull un interval [t1, t2] que es porta al màxim.

Umbral doble 
Representació umbral doble
LUT
[modifica]La LUT defineix un vector, el qual els seus valors indiquen la sortida esperada per cada nivell d'entrada. Els valors dels píxels de la imatge original indexen els nous valors. És a dir, els valors dels píxels de la imatge original corresponen a un índex d'un vector, de manera que els valors dels píxels de la imatge transformada seran els valors d'aquests índexs.
Transformacions lineals
[modifica]Es transforma una imatge I amb un rang de valors determinat en una nova imatge I' = g(I) amb un rang, on g és una funció lineal.
Hi ha dos transformacions lineals:
- Negatiu. Consisteix en invertir el valor dels nivells de grisos de la imatge original, de forma que, en els extrems, el blanc passarà a ser negre i el negre, blanc. La seva funció de transformació és: , on I és la imatge original i x i y són les coordenades del píxel.
- Maximització del contrast. Consisteix en aplicar una transformació lineal de tal manera que els valors ocupin tot el rang possible, produint-se un "estirament" de l'histograma. La seva funció de transformació és: .

Exemple de maximització del contrast
Transformacions no lineals
[modifica]Les transformacions lineals modifiquen el rang de la imatge. En canvi, les transformacions no lineals modifiquen els valors dins del rang de la imatge.
Existeixen dos tipus de transformacions no lineals:
- Logarítmiques. Realça els píxels foscos sense saturar els píxels brillants. La seva transformació és: .

Representació logaritme - Exponencials. Realça els píxels brillants sense saturar els píxels foscos. La seva transformació és: .

Representació exponencial
Operacions lògiques
[modifica]Es realitza un tipus d'operació lògica entre els bits de cada píxel i els d'una certa màscara binària. Els diferents tipus d'operacions lògiques que es troben són: AND, OR, NOT, XOR. Per exemple, l'AND lògic entre una imatge i la constant 11110000 realitza una recuantització uniforme d'una imatge de 256 nivells a únicament 16 nivells.[2]

D'altres operacions lògiques amb bits són els desplaçaments a l'esquerra i a la dreta de bits, que és equivalent al producte i divisió, respectivament, pel producte de 2.
Equalització
[modifica]L'equalització persegueix que tots els nivells de grisos tinguin la mateixa freqüència d'aparició. La manera d'aconseguir-ho és amb una LUT que ajusti l'histograma acumulat de la imatge original al rang de nivells que hi ha. La transformació és: .[2]

Existeixen variacions de l'equalització:
- Equalització local. Es realitza la mateixa operació en una finestra centrada en cada píxel.
- Equalització logarítmica. S'eleva l'histograma acumulat a una constant, canviant la forma de l'histograma final.
Transformacions aritmètiques
[modifica]En les transformades puntuals es realitza una transformació píxel a píxel d'una imatge. Aleshores, en el cas de les transformacions aritmètiques, la imatge transformada és el resultat d'aplicar, punt a punt, un operador, que pot ser una operació lògica o aritmètica, entre dues imatges.
,
on ○ és qualsevol operació lògica o aritmètica, com pot ser:
- Suma
- Resta
- Producte
- Divisió
- AND, OR, XOR
Filtres
[modifica]Els filtres digitals són utilitzats per:
- Suavitzar una imatge, és a dir, reduir les variacions d'intensitat entre els píxels veïns.
- L'eliminació del soroll, modificant els píxels amb un nivell d'intensitat molt diferent al del seus veïns. D'aquesta manera es redueix la informació no desitjada que contamina la imatge.
- Relaçar una imatge amb l'augment de les variacions d'intensitat.
- La detecció de les vores, de manera que es detecta aquells píxels on es produeixen un canvi brusc d'intensitat.[3]
Per tant, els filtres són operacions que s'apliquen als píxels d'una imatge digital per tal d'optimitzar-la, emfatitzar certa informació o aconseguir un efecte especial.
Els filtres digitals poden ser classificats en:
- Filtres en el domini de l'espai.
- Filtres en el domini de freqüències.
Filtres en el domini de l'espai
[modifica]Els filtres en el domini de l'espai són aquells filtres que treballen directament sobre els píxels d'una imatge. Les operacions dels filtres espacials es definieixen en un entorn dels píxels veïns del punt a transformar. És a dir, per aplicar una operació sobre un punt (x,y), s'ha de tenir en compte l'entorn d'aquest, que seran els veïns.[4]
Els filtres en el domini espacial es poden classificar en:
Els filtres lineals consisteixen en passar per cada un dels píxels d'una imatge amb una màscara i per cada un dels píxels es realitza una suma ponderada dels valors dels píxels veïns pels pesos de la màscara. L'operació que es realitza donada un a imatge f(x,y) i una màscara w(x,y) és la següent:
El procés de passar per cada un dels píxels i realitzar aquestes sumes ponderades rep el nom de convolució.
Existeixen diferents filtres lineals, com poden ser:
| Filtres lineals | Utilitat | Implementació Matlab | Exemple |
|---|---|---|---|
| Suavitzat | Redueix les variacions locals d'intensitat, encara que es pot adquirir soroll. | h = ones(2*M+1, 2*N+1)/((2*M+1, 2*N+1));
im2 = imfilter(im, h, 'conv'); %M i N són paràmetres que són assignats per l'usuari. %im és la imatge original. |
  |
| Vores | Senyala les variacions locals d'intesitat, quan aquestes són deguts als contorns dels objectes. | h = 0.5*[1 0 -1];
h = h'; im2 = conv2(double(im), h); %im és la imatge original. |
  |
| Filtre gaussià | S'utilitza per emborronar imatges i eliminar el soroll. | im2 = imgaussfilt(im);
%im és la imatge original. |
  |
Els filtres no lineals no poden ser expressats amb convolucions ni amb manipulacions del contingut freqüencial, és a dir, els valors d'entrada produeixen valors de sortida que no són translacions lineals.
Els diferents filtres no lineals que hi ha són, entre altres:
- Els filtres d'ordre de prioritat, els quals hi ha de tres tipus:
- Filtre de mediana: Selecciona el valor que queda al mig dels valors dels píxels veïns ordenats que estan dins d'una màscara. Per tal d'eliminar el soroll salt-and-pepper (el soroll salt-and-pepper és que alguns píxels s'apaguen de manera aleatòria i d'altres s'encenen).
- Filtre de màxim: Selecciona el valor més gran dels diferents veïns, els quals estan ordenats dins d'una màscara. Aquest filtre és molt útil per l'eliminació del soroll pepper, que són els píxels que estan apagats.
- Filtre de mínim: És el mateix procediment que en el cas del filtre de màxim, però seleccionant el valor mínim. Per tant, elimina el soroll salt, que són els píxels que s'encenen.
- Punt mitjà de l'entorn de veïnatge: La imatge es genera a base de trobar la mitjana dels píxels màxim i mínim del conjunt formats pels píxels veïns d'un punt, reduint la nitidesa i eliminant el soroll uniforme.
- Alpha-Media de l'entorn de veïnatge: La nova imatge es genera trobant la mitjana dels píxels veïns sense tenir en compte ni el màxim ni el mínim. S'utilitza per tractar imatges amb soroll gaussià i aleatori.
- Mitjana geomètrica de l'entorn de veïnatge: Es realitza el producte dels valors dels píxels elevats a . Aquest filtre treballa també molt bé el soroll gaussià.
Filtres en el domini de freqüències
[modifica]En el cas de filtres en el domini de freqüències, el processament de la imatge es fa a partir d'una transformada de la imatge, el qual la més utilitzada és la transformada de Fourier. Un cop s'ha tractat aquesta imatge, es realitza la transformada inversa per tal d'obtenir els resultats.[5]
Els filtres en el domini de la freqüència s'utilitzen principalment per eliminar altes o baixes freqüències d'una imatge, de tal manera que es suavitzaria la imatges o realçar o detectar vores.
Els pasos que es segueixen per tal d'eliminar aquestes freqüències són:

- Es multiplica la imatge d'entrada per .
- Es transforma la imatge en el seu domini de freqüència.
- Es multiplica aquest domini per un filtre de freqüència. Això és el que es coneix com a Teorema de la Convolució, on F(u,v) és el domini de freqüència i H(u,v), el filtre a aplicar.
- Es calcula la transformada inversa del resultat.
Existeixen diversos tipus de filtres en el domini de la freqüència, que el que es fa és deixar passar més o menys components freqüencials. Aleshores, els diferents filtres són:

- Filtres passa baix: Atenuen o eliminen els components d'alta freqüència en el domini de Fourier sense alterar les baixes freqüències, és a dir, "deixa passar" les freqüències baixes.
- Filtres passa alt: Atenuen o eliminen els components de baixa freqüència en el domini de Fourier sense alterar les altes freqüències, és a dir, "deixa passar" les freqüències altes.
- Filtres passa banda: S'eliminen els components d'unes freqüències intermedies, és a dir, atenuen freqüències molt altes o molt baixes mantenint un rang intermedi.
Reducció de soroll d'una imatge amb Morfologia
[modifica]La morfologia matemàtica es va establir en els anys 70 a partir de Jean Serra i Georges Mathéron a partir d'estudis d'imatges de microscopia de materials, petrografia, entre d'altres. En si mateixa, és un marc de processat de senyal i imatges autocontingut.
Es poden distingir dos tipus de morfologia matemàtica, els que s'apliquen a imatges binàries (aquelles imatges, les quals els píxels tenen valors 0 o 1, és a dir, blanc o negre) i els que s'apliquen a imatges en nivell de grisos.
Aquestes imatges seran manipulades per uns conjunts anomenats elements estructurants. Aquests elements estructurants sean l'equivalent de les finestres lliscants, filtres, màscares... El centre de l'element estructural és el valor del punt que es vol modificar.[6]
Respecte la morfologia matemàtica binària, les diferents operacions que hi ha són:
- Dilatació: Es recorre tota la imatge amb l'element estructurant i s'afegeix a la imatge el resultat del píxel central de l'element estructurant si l'element estructurant intersecta amb la imatge. L'efecte que s'obté és l'agregació de material, és a dir, es produeix una expansió. S'aconsegueix amb un AND lògic. L'operació és: , on X representa la imatge i B, l'element estructurant.

- Erosió: Es mou l'element estructurant per tota la imatge i el resultat de l'erosió serà aquelles posicions del centre de l'element estructurant en la que tot l'element estructurant estigui en el conjunt inicial. S'aconsegueix amb un OR lògic. L'operació és: , on X representa la imatge i B, l'element estructurant.

- Opening: En aquesta operació, primer es fa una erosió, per tal de treure material, i després s'aplicarà una dilatació. Això fa que s'intenti emplenar el que ha estat eliminat per l'erosió, però eliminat elements petits i prims. Aquest procés elimina petites illes, ismes i caps. L'operació és: = () .

- Closing: En aquest cas, primer es dilata per tal d'agregar material i després s'erosiona per intentar tenir les proporcions anteriors, però de manera que s'hagi tancat forats, eliminant petits llacs, canals i badies. L'operació és: = () .

Aquestes operacions poden ser utilitzades per la suavització de la forma, filtrat del soroll, segmentació de microestructures, entre d'altres.
Respecte la morfologia matemàtica en nivell de grisos, es defineix l'element estructurant i si es vol fer una dilatació s'hauria de quedar amb el valor màxim d'aquest element estructurant. En canvi, si es vol fer una erosió, es queda amb el valor mínim.
A més, també es pot fer el gradient en el nivell de grisos, per tal d'obtenir els contorns. Aquesta operació es realitza amb la resta entre la dilatació i l'erosió, encara que també es pot obtenir amb la resta entre la imatge en escala de grisos i l'erosió o amb la resta entre la dilatació i la imatge en escala de grisos. Les operacions que es poden realitzar són:
L'opening residue és una altra operació que es pot realitzar amb una imatge en escala de grisos. L'operació que es realitza és una resta entre la imatges en escala de grisos i el opening. D'aquesta manera, s'obté les part de dalt de les funcions, és a dir, es pot detectar crestes i pics, per exemple, d'un relleu. L'operació és:
Transformacions geomètriques
[modifica]Les transformacions geomètriques modifiquen la relació espacial entre píxels.[7] En terme del processament digital d'imatges, una transformació geomètrica consisteix en dos passos:
- Computation of Mapping. Es troba l'equació que relaciona els sistemes de coordenades de la imatge original i de la resultant.
- Resampling o interpolació. Assignar valors d'intesitat dels píxles en la imatge resultant.
Aquest tipus de transformacions serveixen per:
- Eliminar distorsions a causa de l'òptica, el tipus de sensor, el punt de vista...
- Introduir distorsions per registrar imatges, estimar moviment, crear imatges panoràmiques, etc.
- Reconeixement de formes invariant a certes transformacions.[8]
Les principals transformacions que hi ha són:
| Transformació | Matriu | Exemple |
|---|---|---|
| Translació | Aquesta transformació no requereix de matriu, ja que es realitza un desplaçament de la imatge |  |
| Rotació | , on θ és l'angle amb què es vol rodar la imatge |  |
| Escalat uniforme o isotròpic | , s és el valor per ampliar o reduir la imatge |  |
| Escalat no uniforme o anisotròpic | , on és un valor per modificar la coordenada x del píxel i és un valor diferent per modificar la coordenada y |  |
| Reflexió | , per a realitzar una reflexió horitzontal
, per a realitzar una reflexió vertical Com es pot veure, aquests casos són particulars de l'escalat no uniforme. |
 |
| Inclinació | , on a és un valor introduït per indicar la inclinació |  |
Existeixen més transformacions, encara que les altres és una combinació de les ja mencionades. Com pot ser les transformacions afins, que són les més utilitzades per la seva representació i maneig matricial, que són una combinació de translació, rotació, escalat uniforme, escalat no uniforme i inclinació.
Una transformació afí és aquella en la que les coordenades del punt de la imatge transformada són expressades linealment en termes de les del punt original. És a dir, la transformació ve donada per:
que la seva representació matricial és:

Aquesta transformació conserva les línies rectes i paral·leles i els ratios de longituds al llarg de les rectes.
Transformacions
[modifica]Vegeu també
[modifica]- Visió artificial
- Detecció de tall
- Detecció de característiques
- Matlab, programari matemàtic que permet realitzar processament digital d'imatges
Referències
[modifica]- ↑ «Tema 1. Histogramas y transformaciones puntuales - Histogramas y transformaciones puntuales PID_». [Consulta: 18 juny 2022].
- ↑ 2,0 2,1 2,2 «Processat d'imatges». Universitat Autònoma de Barcelona. [Consulta: 18 juny 2022].[Enllaç no actiu]
- ↑ 3,0 3,1 «Tema 3:Filtros». Arxivat de l'original el 12 d’agost 2022. [Consulta: 28 maig 2022].
- ↑ «Sistemes lineals (Filtrat lineal)». Universitat Autònoma de Barcelona. [Consulta: 28 maig 2022].[Enllaç no actiu]
- ↑ «Tema 3: Procesamiento en el dominio de la frecuencia» (en castellà). [Consulta: 28 maig 2022].
- ↑ «Filtratge no lineal». Universitat Autònoma de Barcelona. [Consulta: 29 maig 2022].[Enllaç no actiu]
- ↑ «TRANSFORMACIONES GEOMÉTRICAS SOBRE IMÁGENES DIGITALES» (en castellà). Universidad Distrital Francisco José de Caldas. [Consulta: 17 juny 2022].
- ↑ «T10. Transformaciones geométricas» (en castellà). Universitat Jaume-I. [Consulta: 17 juny 2022].





![{\displaystyle g(n)=255\left[{\frac {I(x,y)-min(I(x,y))}{max(I(x,y))-min(I(x,y))}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a486c9f3576b8914e7105fb91f24ebe7f3668018)





![{\displaystyle g(n)={\frac {\sharp levels}{\sharp pic}}\sum {H[i]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b94cc7ce4d72fff627273b8276f50a5b6b5725e2)























