Punt de l'infinit

Fig. 1: la recta projectiva real (ℝP¹), amb el punt de l'infinit ${\displaystyle \textstyle \infty }$, genera una corba tancada

El punt de l'infinit, punt a l'infinit o punt impropi és una entitat topològica i geomètrica que s'introdueix a manera de tancament o frontera infinita del conjunt dels nombres reals. Quan s'afegeix a la recta real, genera una corba tancada (vegeu fig. 1) coneguda com a recta projectiva real, ${\displaystyle \mathbb {R} P^{1}}$, que no és equivalent a la recta real ampliada, que té dos punts diferents en l'infinit:

${\displaystyle {\overline {\mathbb {R} }}=\mathbb {R} \cup \{\infty \}}$

Topologia T

Perquè el punt de l'infinit representi efectivament l'infinit real es defineix en ${\displaystyle {\overline {\mathbb {R} }}}$ la topologia ${\displaystyle {\overline {T}}}$ formada per tots els conjunts:

• A, que són oberts de ${\displaystyle \mathbb {R} }$
• B, que són complementaris de conjunts compactes (tancats i fitats) de ${\displaystyle \mathbb {R} }$

Els conjunts A són els oberts de ${\displaystyle {\overline {\mathbb {R} }}}$ que no contenen el ${\displaystyle \infty }$, mentre que els conjunts B són els que sí el contenen.

Sigui ${\displaystyle x_{n}\in \mathbb {R} }$ una successió de nombres reals tals que ${\displaystyle \lim _{n\to \infty }x_{n}=\infty }$. Dins del conjunt dels nombres reals, això vol dir únicament que:

${\displaystyle \forall K>0\ \exists m\in \mathbb {N} |si\ n>m\Rightarrow x_{n}\notin [-K,K]}$

Però aquesta mateixa condició implica en ${\displaystyle {\overline {\mathbb {R} }}}$ que:

${\displaystyle \forall B|\infty \in B\ \exists m\in N|si\ n>m\Rightarrow x_{n}\in B}$

És a dir, que en ${\displaystyle {\overline {\mathbb {R} }}}$ s'escriu també ${\displaystyle \lim _{n\to \infty }x_{n}=\infty }$. No obstant això, només en ${\displaystyle {\overline {\mathbb {R} }}}$ es pot dir que la successió ${\displaystyle x_{n}\,}$ convergeix, ja que ${\displaystyle \infty \notin \mathbb {R} }$ .

En el pla complex

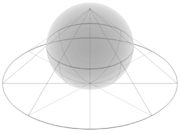
	Fig. cp1: projecció estereogràfica del pla complex estès sobre l'esfera de Riemann
	Fig. cp2: l'esfera de Riemann pot ser visualitzada com el pla complex embolicat al voltant d'una esfera

El punt de l'infinit també pot afegir-se al pla complex, ${\displaystyle \mathbb {C} ^{1}}$, de manera que es transformi en una superfície tancada (vegeu fig. cp1 i fig. cp2), la recta projectiva complexa ${\displaystyle \mathbb {C} P^{1}}$, també anomenada esfera de Riemann, una esfera sobre el pla complex i des del pol superior del qual es projecta la resta de punts de l'esfera sobre el pla complex D'aquesta manera, s'estableix una bijectivitat en la qual a cada punt de l'esfera en correspon un del pla complex. L'homòleg del punt des del qual projectem estereogràficament es converteix en el punt de l'infinit.

Rectes paral·leles en ℝ²

Igual que dues rectes assecants comparteixen un punt, dues rectes paral·leles comparteixen una direcció, per la qual cosa aquestes direccions també són conegudes com a punts impropis d'aquestes rectes en les quals es troben. Per exemple, en ${\displaystyle \mathbb {R} ^{2}}$ no és possible determinar amb exactitud la posició del punt de l'infinit mitjançant unes coordenades absolutes ${\displaystyle (x,y)\,}$. Per aconseguir-ho, s'acudeix a les coordenades homogènies ${\displaystyle (x',y',w)\,}$, en què ${\displaystyle x'\,}$ i ${\displaystyle y'\,}$ representen la direcció del vector director de la recta. Les anteriors coordenades absolutes ${\displaystyle (x,y)\,}$ venen donades per:

${\displaystyle (x,y)=({x' \over w},{y' \over w})}$

El punt ${\displaystyle (4,6)\,}$ podria representar-se, per exemple, com ${\displaystyle (8,12,2)\,}$ o com ${\displaystyle (2,3,{\tfrac {1}{2}})}$. La representació del punt de l'infinit s'obté igualant ${\displaystyle w=0\,}$, així:

${\displaystyle (x',y',0)\,}$

El punt de l'infinit de l'eix OX seria el ${\displaystyle (1,0,0)\,}$, el ${\displaystyle (2,0,0)\,}$, etc.

Vegeu també

• Coordenades homogènies.
• Esfera de Riemann.
• Punt de fuga.