Retropropagació en el temps

La retropropagació a través del temps (BPTT) és una tècnica basada en gradients per entrenar certs tipus de xarxes neuronals recurrents, com les xarxes Elman. L'algorisme va ser derivat de manera independent per nombrosos investigadors.^[1][2]

Algorisme

BPTT desplega una xarxa neuronal recurrent a través del temps.

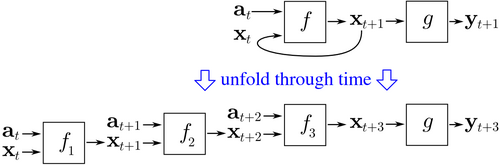
Les dades d'entrenament per a una xarxa neuronal recurrent són una seqüència ordenada de ${\displaystyle k}$ parells entrada-sortida, ${\displaystyle \langle \mathbf {a} _{0},\mathbf {y} _{0}\rangle ,\langle \mathbf {a} _{1},\mathbf {y} _{1}\rangle ,\langle \mathbf {a} _{2},\mathbf {y} _{2}\rangle ,...,\langle \mathbf {a} _{k-1},\mathbf {y} _{k-1}\rangle }$. S'ha d'especificar un valor inicial per a l'estat ocult ${\displaystyle \mathbf {x} _{0}}$, normalment escollit per ser un vector zero.^[3]

BPTT comença desplegant una xarxa neuronal recurrent en el temps. La xarxa desplegada conté ${\displaystyle k}$ entrades i sortides, però cada còpia de la xarxa comparteix els mateixos paràmetres. Aleshores, s'utilitza l'algoritme de retropropagació per trobar el gradient de la funció de pèrdua respecte a tots els paràmetres de la xarxa.

Considereu un exemple de xarxa neuronal que conté una capa recurrent ${\displaystyle f}$ i una capa d'alimentació anticipada ${\displaystyle g}$. Hi ha diferents maneres de definir el cost de la formació, però el cost agregat és sempre la mitjana dels costos de cadascun dels passos de temps. El cost de cada pas de temps es pot calcular per separat. La figura anterior mostra com és el cost en el moment ${\displaystyle t+3}$ es pot calcular, desplegant la capa recurrent ${\displaystyle f}$ durant tres passos de temps i afegint la capa de feedforward ${\displaystyle g}$. Cada instància de ${\displaystyle f}$ a la xarxa desplegada comparteix els mateixos paràmetres. Així, el pes s'actualitza en cada cas ( ${\displaystyle f_{1},f_{2},f_{3}}$ ) es sumen.^[4]

Pseudocodi

A continuació es mostra el pseudocodi d'una versió truncada de BPTT, on conté les dades d'entrenament ${\displaystyle n}$ parells d'entrada-sortida, i la xarxa es desplega per ${\displaystyle k}$ passos de temps:

Back_Propagation_Through_Time(a, y) // a[t] és l'entrada en el temps t. y[t] és la sortida

Desplegueu la xarxa per contenir k instàncies de f

fer fins que es compleixi el criteri d'aturada: x := el vector de magnitud zero // x és el context actual

per a t de 0 a n − k do // t és temps. n és la durada de la seqüència d'entrenament Estableix les entrades de xarxa a x, a[t], a[t+1],... , a[t+k−1]

p := propagar cap endavant les entrades a tota la xarxa desplegada

e := y[t+k] − p; // error = objectiu − predicció Propaga l'error, e, enrere a tota la xarxa desplegada Suma els canvis de pes en les k instàncies de f. Actualitzeu tots els pesos en f i g.

x := f(x, a[t]); // calcula el context per al següent pas de temps

Avantatges

El BPTT acostuma a ser significativament més ràpid per entrenar xarxes neuronals recurrents que les tècniques d'optimització de propòsit general com l'optimització evolutiva.^[5]

Inconvenients

BPTT té dificultats amb els òptims locals. Amb les xarxes neuronals recurrents, els òptims locals són un problema molt més significatiu que amb les xarxes neuronals feed-forward.^[6] La retroalimentació recurrent en aquestes xarxes tendeix a crear respostes caòtiques a la superfície d'error que fan que els òptims locals es produeixin amb freqüència i en llocs pobres de la superfície d'error.

Referències

1. Mozer, M. C.. «A Focused Backpropagation Algorithm for Temporal Pattern Recognition». A: Chauvin. Backpropagation: Theory, architectures, and applications (en anglès). Hillsdale, NJ: Lawrence Erlbaum Associates, 1995, p. 137–169. 
2. Werbos, Paul J. Neural Networks, 1, 4, 1988, pàg. 339–356. DOI: 10.1016/0893-6080(88)90007-x.
3. «9.7. Backpropagation Through Time — Dive into Deep Learning 1.0.3 documentation» (en anglès). [Consulta: 1r febrer 2025].
4. «Backpropagation through time (BPTT)» (en anglès). [Consulta: 1r febrer 2025].
5. Sjöberg, Jonas; Zhang, Qinghua; Ljung, Lennart; Benveniste, Albert; Delyon, Bernard Automatica, 31, 12, 1995, pàg. 1691–1724. DOI: 10.1016/0005-1098(95)00120-8.
6. M.P. Cuéllar and M. Delgado and M.C. Pegalajar. «An Application of Non-Linear Programming to Train Recurrent Neural Networks in Time Series Prediction Problems». A: Enterprise Information Systems VII (en anglès). Springer Netherlands, 2006, p. 95–102. DOI 10.1007/978-1-4020-5347-4_11. ISBN 978-1-4020-5323-8.