Selecció de característiques

La selecció de característiques és el procés de selecció d'un subconjunt de característiques rellevants (variables, predictors) per utilitzar-les en la construcció de models. La estilometria i l'anàlisi de microarrays d'ADN són dos casos en què s'utilitza la selecció de característiques. S'ha de distingir de l'extracció de característiques.[1]

Les tècniques de selecció de característiques s'utilitzen per diversos motius:

  • simplificació dels models per fer-los més fàcils d'interpretar pels investigadors/usuaris,[2]
  • temps d'entrenament més curts,
  • per evitar la maledicció de la dimensionalitat,[3]
  • millorar la compatibilitat de les dades amb una classe de model d'aprenentatge,[4]
  • codifica les simetries inherents presents a l'espai d'entrada.[5][6][7][8]
    Mètode de filtre per a la selecció de funcions

La premissa central quan s'utilitza una tècnica de selecció de característiques és que les dades contenen algunes característiques que són redundants o irrellevants i, per tant, es poden eliminar sense incórrer en molta pèrdua d'informació.[9] Redundant i irrellevant són dues nocions diferents, ja que

Mètode d'embolcall per a la selecció de funcions

una característica rellevant pot ser redundant en presència d'una altra característica rellevant amb la qual està fortament correlacionada.

L'extracció de característiques crea noves característiques a partir de les funcions de les característiques originals, mentre que la selecció de característiques retorna un subconjunt de les característiques. Les tècniques de selecció de característiques s'utilitzen sovint en dominis on hi ha moltes característiques i comparativament poques mostres (o punts de dades).

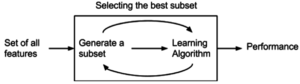
Un algorisme de selecció de característiques es pot veure com la combinació d'una tècnica de cerca per proposar nous subconjunts de característiques, juntament amb una mesura d'avaluació que puntua els diferents subconjunts de

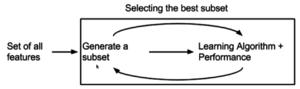
Mètode incrustat per a la selecció de funcions

característiques. L'algorisme més senzill és provar cada possible subconjunt de característiques trobant la que minimitzi la taxa d'error. Es tracta d'una cerca exhaustiva de l'espai i és insoluble computacionalment per a tots els conjunts de característiques menys el més petit. L'elecció de la mètrica d'avaluació influeix molt en l'algorisme, i són aquestes mètriques d'avaluació les que distingeixen entre les tres categories principals d'algoritmes de selecció de característiques: embolcalls, filtres i mètodes incrustats.

Referències

[modifica]
  1. ↑ Sarangi, Susanta; Sahidullah, Md; Saha, Goutam Digital Signal Processing, 104, 9-2020, pàg. 102795. arXiv: 2007.10729. DOI: 10.1016/j.dsp.2020.102795.
  2. ↑ Gareth James. An Introduction to Statistical Learning (en anglès). Springer, 2013, p. 204.  Arxivat 2019-06-23 a Wayback Machine.
  3. ↑ Kramer, Mark A. (en anglès) AIChE Journal, 37, 2, 1991, pàg. 233–243. DOI: 10.1002/aic.690370209. ISSN: 1547-5905.
  4. ↑ Kratsios, Anastasis; Hyndman, Cody Journal of Machine Learning Research, 22, 92, 2021, pàg. 1–51. ISSN: 1533-7928.
  5. ↑ Persello, Claudio. «Relevant and invariant feature selection of hyperspectral images for domain generalization». A: 2014 IEEE Geoscience and Remote Sensing Symposium (en anglès). IEEE, juliol 2014, p. 3562–3565. DOI 10.1109/igarss.2014.6947252. ISBN 978-1-4799-5775-0. 
  6. ↑ Hinkle, Jacob; Muralidharan, Prasanna; Fletcher, P. Thomas; Joshi, Sarang (en anglès) Computer Vision – ECCV 2012 [Berlin, Heidelberg], 7574, 2012, pàg. 1–14. arXiv: 1201.2395. DOI: 10.1007/978-3-642-33712-3_1.
  7. ↑ Yarotsky, Dmitry (en anglès) Constructive Approximation, 55, 30-04-2021, pàg. 407–474. arXiv: 1804.10306. DOI: 10.1007/s00365-021-09546-1. ISSN: 1432-0940.
  8. ↑ Hauberg, Søren; Lauze, François; Pedersen, Kim Steenstrup (en anglès) Journal of Mathematical Imaging and Vision, 46, 1, 01-05-2013, pàg. 103–120. DOI: 10.1007/s10851-012-0372-9. ISSN: 1573-7683.
  9. ↑ Kratsios, Anastasis; Hyndman, Cody Journal of Machine Learning Research, 22, 08-06-2021, pàg. 10312. Bibcode: 2015NatSR...510312B. DOI: 10.1038/srep10312. PMC: 4437376. PMID: 25988841.