Cikcak lemma

Cikcak lemma v matematice, zvláště v homologické algebře, postuluje existenci určité dlouhé exaktní posloupnosti v grupách homologií určitých řetězcových komplexů. Výsledek platí v každé Abelova kategorie.

Tvrzení

V abelovské kategorii (např. v kategorii abelovských grup nebo v kategorii vektorových prostorů nad daným tělesem), nechť ${\displaystyle ({\mathcal {A}},\partial _{\bullet }),({\mathcal {B}},\partial _{\bullet }')}$ a ${\displaystyle ({\mathcal {C}},\partial _{\bullet }'')}$ jsou řetězcové komplexy, které vyhovují následující krátké exaktní posloupnosti:

${\displaystyle 0\longrightarrow {\mathcal {A}}\mathrel {\stackrel {\alpha }{\longrightarrow }} {\mathcal {B}}\mathrel {\stackrel {\beta }{\longrightarrow }} {\mathcal {C}}\longrightarrow 0}$

Tato posloupnost je zkratkou následujícího komutativního diagramu:

kde řádky jsou exaktní posloupnosti a každý sloupec je řetězcový komplex.

Cikcak lemma říká, že existuje kolekce hraničních zobrazení

${\displaystyle \delta _{n}:H_{n}({\mathcal {C}})\longrightarrow H_{n-1}({\mathcal {A}}),}$

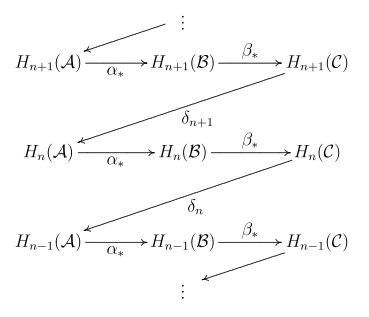
díky níž je následující posloupnost exaktní:

Zobrazení ${\displaystyle \alpha _{*}^{}}$ a ${\displaystyle \beta _{*}^{}}$ jsou obvyklá zobrazení indukovaná homologií. Hraniční zobrazení ${\displaystyle \delta _{n}^{}}$ jsou vysvětlený níže. Jméno lemmatu vychází z „cikcak“ chování zobrazení v posloupnosti. Jiná verze cikcak lemmatu je známa jako „hadí lemma“ (ta vytahuje podstatu důkazu cikcak lemmatu uvedeného níže).

Konstrukce hraničních zobrazení

Zobrazení ${\displaystyle \delta _{n}^{}}$ jsou definovány pomocí standardních argumentů diagramatického nahánění. Nechť ${\displaystyle c\in C_{n}}$ reprezentuje třída v ${\displaystyle H_{n}({\mathcal {C}})}$, tak ${\displaystyle \partial _{n}''(c)=0}$. Z exaktnosti řádku vyplývá, že ${\displaystyle \beta _{n}^{}}$ je surjektivní, takže musí existovat nějaké ${\displaystyle b\in B_{n}}$ s ${\displaystyle \beta _{n}^{}(b)=c}$. Díky komutativitě digramu

${\displaystyle \beta _{n-1}\partial _{n}'(b)=\partial _{n}''\beta _{n}(b)=\partial _{n}''(c)=0.}$

z exaktnosti

${\displaystyle \partial _{n}'(b)\in \ker \beta _{n-1}=\mathrm {im} \;\alpha _{n-1}.}$

Díky tomu, protože ${\displaystyle \alpha _{n-1}^{}}$ je injektivní, existuje jediný prvek ${\displaystyle a\in A_{n-1}}$ takový, že ${\displaystyle \alpha _{n-1}(a)=\partial _{n}'(b)}$. To je cyklus, protože ${\displaystyle \alpha _{n-2}^{}}$ je injektivní a

${\displaystyle \alpha _{n-2}\partial _{n-1}(a)=\partial _{n-1}'\alpha _{n-1}(a)=\partial _{n-1}'\partial _{n}'(b)=0,}$

protože ${\displaystyle \partial ^{2}=0}$. Tj. ${\displaystyle \partial _{n-1}(a)\in \ker \alpha _{n-2}=\{0\}}$. To znamená, že ${\displaystyle a}$ je cyklus, který reprezentuje nějakou třídu v ${\displaystyle H_{n-1}({\mathcal {A}})}$. Nyní můžeme definovat

${\displaystyle \delta _{}^{}[c]=[a].}$

Jsou-li definována hraniční zobrazení, můžeme ukázat, že jsou dobře definovaná (tj. nezávislá na volbě c a b). Důkaz používá podobné argumenty při diagramatickém nahánění jako výše. Tyto argumenty se také používají, pro důkaz, že posloupnost v homologii je exaktní na každé grupě.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Zig-zag lemma na anglické Wikipedii.

• HATCHER, Allen, 2002. Algebraic Topology. [s.l.]: Cambridge University Press. Dostupné online. ISBN 0-521-79540-0. 
• LANG, Serge, 2002. Algebra. 3., revidované vyd. Svazek 211. New York: Springer-Verlag. (Graduate Texts in Mathematics). ISBN 978-0-387-95385-4. 
• MUNKRES, James R., 1993. Elements of Algebraic Topology. New York: Westview Press. ISBN 0-201-62728-0. 

Související články

• Mayerova–Vietorisova posloupnost