Gaussova funkce

Grafy normalizovaných gaussovských funkcí s různými parametry

Gaussova funkce pojmenovaná po matematikovi Carlu Friedrichu Gaussovi je reálná funkce jedné reálné proměnné ${\displaystyle x}$ se třemi parametry ${\displaystyle a,\mu ,\sigma }$ ve tvaru

${\displaystyle f\left(x\right)=ae^{-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}}\,.}$

Čísla ${\displaystyle a}$ a ${\displaystyle \sigma }$ musí být kladná, ${\displaystyle \mu }$ je libovolné reálné, ${\displaystyle e}$ je Eulerovo číslo (2,71828...). Graf funkce má v bodě ${\displaystyle x=\mu }$ vrchol o výšce ${\displaystyle a}$, který graf dělí na dvě vzájemně souměrné části – levou rostoucí z 0 a pravou klesající asymptoticky zpět k 0. Parametr ${\displaystyle \sigma }$ určuje šířku „kopce“ ve výšce ${\displaystyle ae^{-1/8}\approx 0{,}8825\,a}$. V polovině výšky má graf šířku ${\displaystyle 2\sigma {\sqrt {2\ln 2}}\approx 2{,}3548\,\sigma }$.

Normalizované funkce

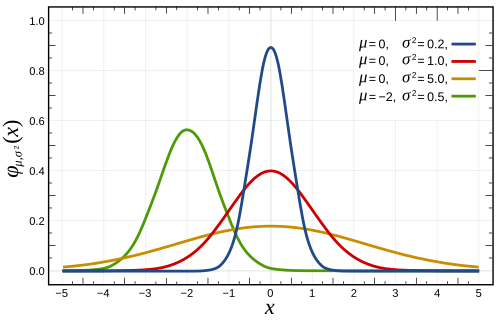
Gaussova funkce se velmi často používá ve významu hustoty pravděpodobnosti. V takovém případě musí být její integrál (plocha pod grafem) přes celý definiční obor roven 1, což představuje pravděpodobnost jistého jevu.

${\displaystyle \int _{-\infty }^{\infty }f\left(x\right)\,{\mathrm {d} }x=1}$

Tuto normalizační podmínku lze splnit vhodnou volbou konstanty ${\displaystyle a}$. Nejjednodušší gaussovskou funkcí je ${\displaystyle g(x)=e^{-x^{2}}}$, jejíž integrál je roven ${\displaystyle {\sqrt {\pi }}}$ (viz Gaussův integrál), takže její normalizovaná verze musí mít tvar

${\displaystyle g_{\mathrm {n} }(x)={\frac {1}{\sqrt {\pi }}}e^{-x^{2}}\,.}$

Parametr ${\displaystyle \mu }$ pouze posouvá graf podél osy ${\displaystyle x}$, takže nemá vliv na hodnotu integrálu. Parametr ${\displaystyle \sigma }$ graf rozšiřuje a integrál se přitom násobí číslem ${\displaystyle \sigma {\sqrt {2}}}$. Obecná normalizovaná Gaussova funkce tedy musí mít tvar

${\displaystyle f_{\mathrm {n} }(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}}\,.}$

Parametr ${\displaystyle \mu }$ má v tomto případě význam střední hodnoty náhodné veličiny a parametr ${\displaystyle \sigma }$ je směrodatná odchylka.

Fourierova transformace

Z matematického a fyzikálního hlediska jsou Gaussovy funkce významné také tím, že při ${\displaystyle \mu =0}$ je Fourierovým obrazem funkce opět Gaussova funkce, obecně s jinými parametry.

${\displaystyle {\hat {f}}(\xi )={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{\infty }f(x)e^{-i\xi x}\,{\mathrm {d} }x=a\sigma e^{-\sigma ^{2}\xi ^{2}/2}}$

Je-li navíc ${\displaystyle \sigma =1}$, je Gaussova funkce obrazem sama sebe (${\displaystyle {\hat {f}}=f}$), takže představuje pevný bod Fourierovy transformace. Ze všech normalizovaných funkcí má tuto vlastnost pouze jediná:

${\displaystyle f_{\mathrm {n} }(x)={\frac {1}{\sqrt {2\pi }}}e^{-x^{2}/2}\,.}$

Odkazy

Související články

• Normální rozdělení

Externí odkazy

• Gaussian Function – Wolfram MathWorld

Portály: Matematika