Halda (datová struktura)

Tento článek je o haldě jako stromové datové struktuře. O haldě jako paměťovém prostoru v počítačových programech pojednává článek Dynamická alokace paměti.

Halda (anglicky heap) je v informatice stromová datová struktura splňující tzv. vlastnost haldy: pokud je B potomek A, pak x(A) >= x(B). To znamená, že v kořenu stromu je vždy prvek s nejvyšším klíčem (klíč udává funkce x). Taková halda se pak někdy označuje jako max heap, halda s reverzním pořadím prvků se analogicky nazývá min heap. Díky této vlastnosti se haldy často používají na implementaci prioritní fronty. Efektivita operací s haldou je klíčová pro mnoho algoritmů.

Operace s haldou

• INSERT - přidání nového prvku do haldy
• DELETE MAX nebo DELETE MIN - vyjmutí kořenu v max heap nebo v min heap
• DELETE(v) - smaže uzel „v“
• MIN, MAX - vrátí minimální resp. maximální klíč v haldě
• DECREASE KEY(v, okolik) - zmenšení klíče uzlu „v“ o hodnotu „okolik“
• INCREASE KEY(v, okolik) - zvětšení klíče uzlu „v“ o hodnotu „okolik“
• MERGE - spojení dvou hald do jedné nové validní haldy obsahující všechny prvky obou původních
• MAKE - dostane pole N prvků a vytvoří z nich haldu

Popis haldy

Haldu bychom mohli tedy definovat jako datovou strukturu splňující dvě základní podmínky:

• lokální podmínku na uspořádání - prvek reprezentující otce je menší než prvek reprezentovaný synem apod.
• strukturální podmínku na stromy, ze kterých jsou vytvořené

Právě podle těchto podmínek se haldy rozdělují na d-regulární, Fibonacciho, Leftist a další (mohou se lišit jak lokální, tak strukturální podmínkou).

Jak již bylo naznačeno, rozlišujeme haldy Min-Heap a Max-Heap.

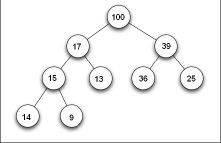
• U Min-Heap jsou klíče dětí jednoho uzlu vždy větší než klíče svého otce. To způsobuje, že na kořenech stromu lze nalézt pouze prvek s minimálním klíčem.
• Opačně je pro Max-Heap stanovena podmínka, že klíče dětí jednoho uzlu musí být vždy menší než klíče jejich otce. Zde se na kořeni stromu vždy nachází prvek s maximálním klíčem.

Příklady Min-Heap a Max-Heap

Min heap

Max heap

Matematicky se u obou variant jedná pouze o rozdíl v jejich opačném pořadí prvků. Protože je definice vzestupně i sestupně libovolná, je pouze otázkou interpretace, zda se v konkrétní implementaci jedná o Min-Heap nebo o Max-Heap.

Obousměrné haldy (Double heaps)

Často se stává, že halda má zobrazit podmínku v obou směrech. V tomto případě se jednoduše vytvoří haldy dvě a uspořádají se podle větší a menší relace. Taková struktura je pak označována jako Double heap nebo krátce Deap.

Při použití Double heaps je třeba dávat pozor na to, že ne každá implementace haldy si pro jednotlivé operace zachová svůj průběh. Například Fibonacciho haldy s konstantním amortizovaným průběhem podporují pouze decreaseKey pro snížení klíčů. Všeobecný changeKey pro změnu klíče, který je vyžadován v případě Double heap, potřebuje ale amortizovaně minimálně logaritmický čas.

Variantou hald, které splňují podmínku haldy pouze částečně, nebo odchylně jsou tzv. Min-Max-Heap. Jedná se o Double heap, které díky odchylné formě podmínky haldy mohou udržovat data pouze v jednom stromu.

Varianty haldy

Existuje mnoho druhů hald s rozdílným průběhem pro různé operace. Příklady hald:

• d-regulární halda, d=2 binární
• Binomiální halda
• Fibonacciho halda
• Leftist halda
• Pairing
• Soft halda
• 2-3 Halda
• Treap
• Beap
• Skew halda
• Q-Halda

Porovnání teoretických hranic složitostí pro jednotlivé varianty

U Pairing, binární a binomiální haldy jde o složitosti v nejhorším případě^[1]. O amortizované složitosti u Fibonacciho a Leftist haldy. O(f) dává asymptotickou horní hranici a Θ(f) je asymptoticky přesná (až na multiplikativní konstantu) složitost. V tabulce předpokládáme použití Min Heap.

Operace	Binární	Binomiální	Fibonacciho	Pairing	Leftist	2-3	Treap	Beap
createHeap	Θ${\displaystyle (1)}$	Θ${\displaystyle (1)}$	Θ${\displaystyle (1)}$	Θ${\displaystyle (1)}$
findMin	Θ${\displaystyle (1)}$	Θ${\displaystyle (\log n)}$ nebo Θ${\displaystyle (1)}$	Θ${\displaystyle (1)}$	Θ${\displaystyle (1)}$	Θ${\displaystyle (1)}$			Θ${\displaystyle (1)}$
deleteMin	Θ${\displaystyle (\log n)}$	Θ${\displaystyle (\log n)}$	Θ${\displaystyle (\log n)}$	Θ${\displaystyle (n)}$	Θ${\displaystyle (\log n)}$	Θ${\displaystyle (\log n)}$	Θ${\displaystyle (\log n)}$	Θ${\displaystyle (\log n)}$
insert	Θ${\displaystyle (\log n)}$	Θ${\displaystyle (\log n)}$	Θ${\displaystyle (1)}$	Θ${\displaystyle (1)}$	Θ${\displaystyle (1)}$ nebo Θ${\displaystyle (\log n)}$	Θ${\displaystyle (1)}$	Θ${\displaystyle (\log n)}$	Θ${\displaystyle (\log n)}$
decrease-key	Θ${\displaystyle (\log n)}$	Θ${\displaystyle (\log n)}$	Θ${\displaystyle (1)}$	Θ${\displaystyle (1)}$	Θ${\displaystyle (1)}$ nebo Θ${\displaystyle (\log n)}$	Θ${\displaystyle (1)}$
merge	Θ${\displaystyle (n)}$	Θ${\displaystyle (\log n)}$	Θ${\displaystyle (1)}$	Θ${\displaystyle (1)}$	Θ${\displaystyle (\log n)}$

Využití haldy

Halda má široké spektrum využití a patří mezi oblíbené datové struktury pro mnoho aplikací.

• Heapsort: řadicí algoritmus.
• Výběrový algoritmus: Hledání minima, maxima nebo obou, mediánu nebo dokonce jakéhokoli k-prvku (to sice lze, ale je to pomalé) a může být prováděno dynamicky.
• implementace Dijkstrova algoritmu - využití jakékoli haldy, ale využití Fibonacciho haldy dává pro řídké grafy lepší časovou složitost.
• implementace Jarníkova algoritmu
• Prioritní fronty: využití haldy pro stanovení front úkolů například u serverů nebo provozních systémů
• Hladové algoritmy: halda představuje ideální datovou strukturu pro tzv. hladové algoritmy, které se řídí lokálními optimalizovanými rozhodnutími.

Implementace haldy

Standard Template Library jazyka C++ poskytuje algoritmy make_heap, push_heap a pop_heap pro binární haldy, které pracují na iterátorech s náhodným přístupem.

Implementace binární haldy

Binární haldy mohou být implementovány jednoduše pomocí pole.

První nebo poslední prvek bude obsahovat kořen. Následující dva prvky pole obsahují jeho potomky. Následující čtyři obsahují další čtyři potomky předchozích dvou potomků, atd. A tak potomci uzlu na pozici n budou na pozici 2n a 2n+1 v polích indexovaných od jedničky nebo 2n+1 a 2n+2 v polích indexovaných od nuly. Vyvažování haldy je prováděno záměnou prvků, které nejsou umístěny ve správném pořadí. Tak, jako můžeme sestavit haldu z pole bez využití další paměti (například pro uzly), heapsort může být také použít pro třídění pole na místě. Další výhoda haldy v některých aplikacích je, že sestavení hald může být prováděno v lineárním čase použitím Tarjanova algoritmu.

Poznámky

1. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest (1990): Introduction to algorithms. MIT Press / McGraw-Hill.

Externí odkazy

• Vizualizace haldy
• [1] (Soubor na stažení)
• [2] Archivováno 7. 2. 2007 na Wayback Machine. (Soubor na stažení)
• Skripta z grafových algoritmů obsahující popis Q-Hald