Impedance

Impedance je komplexní veličina elektrického obvodu vyjádřená reálnou rezistancí a imaginární reaktancí, bránící průchodu elektrického proudu.

Značka: ${\displaystyle Z\,\!}$

Jednotka SI: ohm, značka ${\displaystyle \Omega }$

Vyjádření impedance

Impedance jako komplexní veličina

Komplexní impedanci ${\displaystyle Z}$ vyjádříme v algebraickém (kartézském) tvaru:

${\displaystyle Z=R+jX}$,

kde

• ${\displaystyle R>0}$ je rezistance; měří se v ohmech.
• ${\displaystyle X>0}$ je reaktance; měří se v ohmech.
• ${\displaystyle j\;=\;{\sqrt {-1}}}$ je imaginární jednotka (místo ${\displaystyle i}$ značíme ${\displaystyle j}$),

resp. v goniometrickém (polárním) tvaru:

${\displaystyle \mathbf {Z} =|\mathbf {Z} |(\cos \varphi +\mathrm {j} \sin \varphi )=|\mathbf {Z} |e^{\mathrm {j} \varphi }}$,

kde ${\displaystyle |\mathbf {Z} |={\sqrt {R^{2}+X^{2}}}}$ je absolutní hodnota impedance a ${\displaystyle \varphi =\arctan {({\frac {X}{R}})}}$ je úhel impedance.

Parametry impedance

Harmonický proud a napětí můžeme vyjádřit vztahy:

${\displaystyle i=I_{max}e^{j\omega t}}$; ${\displaystyle u=U_{max}e^{j(\omega t+\phi )}}$ kde ${\displaystyle \phi }$ je fázový posun napětí vůči proudu,

impedanci poté vyjádříme z Ohmova zákona: ${\displaystyle Z={\frac {u}{i}}={\frac {U_{max}}{I_{max}}}e^{j\phi }}$

fázový posun napětí vůči proudu

Odpor

Rezistorem o odporu ${\displaystyle R}$ procházející proud ${\displaystyle i}$ má vůči napětí ${\displaystyle u}$ nulový fázový posun:

${\displaystyle Z_{R}=R}$

Indukčnost

Cívkou o indukčnosti ${\displaystyle L}$ procházející proud ${\displaystyle i}$ indukuje napětí ${\displaystyle u}$:

${\displaystyle u=L{\frac {\operatorname {d} \!i}{\operatorname {d} \!t}}=L{\frac {\operatorname {d} }{\operatorname {d} \!t}}I_{max}e^{j\omega t}=j\omega LI_{max}e^{j\omega t}\,\,\,\,\,}$ tj. ${\displaystyle Z_{L}=j\omega L}$

Kapacita

Kondenzátor o kapacitě ${\displaystyle C}$ se při napětí ${\displaystyle u}$ nabije nábojem ${\displaystyle q}$:

${\displaystyle -q=Cu=\int i\operatorname {d} \!t=\int I_{max}e^{j\omega t}\operatorname {d} \!t={\frac {1}{j\omega }}I_{max}e^{j\omega t}\,\,\,\,\,}$ tj. ${\displaystyle u={\frac {1}{j\omega C}}I_{max}e^{j\omega t}\,\,\,\,\,}$ tj. ${\displaystyle Z_{C}={\frac {1}{j\omega C}}}$

Zapojení impedancí

Sériové zapojení impedancí

${\displaystyle \mathbf {Z} =\mathbf {Z} _{1}+\mathbf {Z} _{2}=(R_{1}+R_{2})+\mathrm {j} (\mathrm {X} _{1}+\mathrm {X} _{2})\quad }$

Paralelní zapojení impedancí

${\displaystyle \mathbf {Z} =\left(\mathbf {Z} _{1}^{-1}+\mathbf {Z} _{2}^{-1}\right)^{-1}={\mathbf {Z} _{1}\mathbf {Z} _{2} \over \mathbf {Z} _{1}+\mathbf {Z} _{2}}\quad }$

Měření impedancí

Při měření impedance musíme napájet obvod vždy střídavým proudem, v případě proudu stejnosměrného bychom měřili pouze reálnou složku impedance.

Měření voltmetrem, ampérmetrem a wattmetrem

Vztahy

Podíl efektivních hodnot napětí a proudu nám dá absolutní hodnotu impedance.

${\displaystyle |\mathbf {Z} |={\frac {U}{I}}}$

Velikost fázového posunu

${\displaystyle \ P=UI\cos \varphi }$

Velikost činného odporu

${\displaystyle P=RI^{2}=>R={\frac {P}{I^{2}}}}$

Velikost reaktance

${\displaystyle X=|\mathbf {Z} |\sin \varphi }$

Velikost vlastní indukčnosti (pro induktivní charakter zátěže)

${\displaystyle L={\frac {X}{2\pi f}}}$

Velikost elektrické kapacity (pro kapacitní charakter zátěže)

${\displaystyle \ C={\frac {1}{2\pi fX}}}$

Hraniční impedance

Velikost hraniční impedance určuje, zda je vhodnější použít zapojení pro malé nebo pro velké impedance.

${\displaystyle |\mathbf {Z_{h}} |\approx {\sqrt {(R_{A}+R_{WP}){\frac {R_{V}R_{WN}}{R_{V}+R_{WN}}}}}}$

${\displaystyle R_{A}}$ - vnitřní odpor ampérmetru

${\displaystyle R_{V}}$ - vnitřní odpor voltmetru

${\displaystyle R_{WP}}$ - vnitřní odpor proudové cívky wattmetru

${\displaystyle R_{WN}}$ - vnitřní odpor napěťové cívky wattmetru

Tato metoda není přesná, protože velikosti jednotlivých složek zjišťujeme více výpočty. Používá se pouze pro orientační měření.

Zapojení pro měření malých impedancí

Zapojení pro měření velkých impedancí

Metoda tří ampérmetrů

Neznámou impedanci ${\displaystyle Z_{x}}$ zapojíme paralelně se známým odporovým normálem ${\displaystyle R_{N}}$. Třemi ampérmetry měříme efektivní hodnoty proudů v jednotlivých větvích i proud celkový. Metoda tří ampérmetrů je nejpřesnější, jsou-li proudy ${\displaystyle I_{R}}$ a ${\displaystyle I_{Z}}$ stejně velké a fázový posun způsobený měřenou impedancí je velký.

Velikost napětí

${\displaystyle \mathbf {U} =\mathbf {Z_{x}} \mathbf {I_{Z}} =R_{N}\mathbf {I_{R}} }$

Velikost absolutní hodnoty impedance

${\displaystyle \mathbf {|Z_{x}|} ={\frac {RI_{R}}{I_{Z}}}}$

Podle prvního Kirchhoffova zákona platí

${\displaystyle \mathbf {I} =\mathbf {I_{R}} +\mathbf {I_{Z}} }$

Podle fázorového diagramu platí pro úhel ${\displaystyle \varphi '}$ kosinová věta

${\displaystyle I^{2}=I_{Z}^{2}+I_{R}^{2}-2I_{R}I_{Z}\cos \varphi '}$

Pro ${\displaystyle \cos \varphi '}$ platí

${\displaystyle \cos \varphi '=-{\frac {I^{2}-I_{Z}^{2}-I_{R}^{2}}{2I_{R}I_{Z}}}}$

Pro úhel ${\displaystyle \varphi }$ platí

${\displaystyle \ \varphi =180-\varphi '}$

Pro ${\displaystyle \cos \varphi }$ platí

${\displaystyle \ \cos \varphi =-\cos \varphi '}$

${\displaystyle \cos \varphi ={\frac {I^{2}-I_{Z}^{2}-I_{R}^{2}}{2I_{R}I_{Z}}}}$

Jednotlivé složky impedance budou mít velikost:

${\displaystyle \ R_{x}=\mathbf {|} Z|\cos \varphi }$

${\displaystyle \ X_{x}=\mathbf {|} Z|\sin \varphi }$

Pro činný výkon na zátěži platí:

${\displaystyle P=U_{Z}I_{Z}\cos \varphi =R_{N}I_{R}I_{Z}{\frac {I^{2}-I_{Z}^{2}-I_{R}^{2}}{2I_{R}I_{Z}}}={\frac {R_{N}}{2}}(I^{2}-I_{R}^{2}-I_{Z}^{2})}$

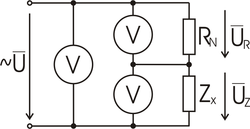
Metoda tří voltmetrů

Měřená impedance ${\displaystyle Z_{x}}$ je zapojena v sérii s odporovým normálem ${\displaystyle R_{N}}$. Pomocí tří voltmetrů měříme efektivní hodnoty úbytků napětí na normálu, na měřené impedanci a napětí celkové.

Podle fázorového diagramu platí pro úhel ${\displaystyle \varphi '}$ kosinová věta

${\displaystyle U^{2}=U_{Z}^{2}+U_{R}^{2}-2U_{R}U_{Z}\cos \varphi '}$

Pro ${\displaystyle \cos \varphi '}$ platí

${\displaystyle \cos \varphi '=-{\frac {U^{2}-U_{Z}^{2}-U_{R}^{2}}{2U_{R}U_{Z}}}}$

Pro úhel ${\displaystyle \varphi }$ platí

${\displaystyle \ \varphi =180-\varphi '}$

Pro ${\displaystyle \cos \varphi }$ platí

${\displaystyle \ \cos \varphi =-\cos \varphi '}$

${\displaystyle \cos \varphi ={\frac {U^{2}-U_{Z}^{2}-U_{R}^{2}}{2U_{R}U_{Z}}}}$

Jednotlivé složky impedance budou mít velikost:

${\displaystyle \ R_{x}=\mathbf {|} Z|\cos \varphi }$

${\displaystyle \ X_{x}=\mathbf {|} Z|\sin \varphi }$

Pro činný výkon na zátěži platí:

${\displaystyle P=U_{Z}I_{Z}\cos \varphi ={\frac {U_{Z}U_{R}}{R_{N}}}{\frac {U^{2}-U_{Z}^{2}-U_{R}^{2}}{2U_{R}U_{Z}}}={\frac {U^{2}-U_{R}^{2}-U_{Z}^{2}}{2R_{N}}}}$

Hraniční impedance

Zda máme použít k měření impedance metodu tří ampérmetrů nebo voltmetrů rozhodne hodnota hraniční impedance. Pro určení její velikosti platí vztah:

${\displaystyle \mathbf {Z_{h}} \approx {\sqrt {R_{A}R_{V}}}}$

${\displaystyle R_{A}}$ - vnitřní odpor ampérmetrů

${\displaystyle R_{V}}$ - vnitřní odpor voltmetrů

Je-li ${\displaystyle |\mathbf {Z_{x}} |<|\mathbf {Z_{h}} |}$, je pro měření vhodnější metoda tří voltmetrů, pro ${\displaystyle |\mathbf {Z_{x}} |>|\mathbf {Z_{h}} |}$ je pro měření vhodnější metoda tří ampérmetrů.

Obecný můstek

Obecný můstek

Jde o obdobu Wheatstoneova můstku pro měření odporů. Pokud je v některé z podmínek rovnováhy zastoupena frekvence, je můstek frekvenčně závislý a lze ho použít nejen k měření impedancí, ale také k měření frekvencí. Pro měření impedancí jsou výhodnější, frekvenčně nezávislé můstky. Střídavé můstky jsou napájeny z oscilátoru. Nulové indikátory (NI) indikují vyvážení můstku. K tomu se nejčastěji používá osciloskop. Abychom omezili vnější rušivé vlivy, musí být můstky pečlivě zemněny a stíněny.

Podmínka rovnováhy

${\displaystyle \mathbf {Z_{1}} \mathbf {Z_{4}} =\mathbf {Z_{2}} \mathbf {Z_{3}} }$

${\displaystyle \mathbf {Z} =R\pm \mathrm {j} X}$

Dosadíme-li za jednotlivé hodnoty impedancí hodnoty v exponenciálním tvaru, bude platit:

${\displaystyle \mathbf {Z_{1}} e^{\mathrm {j} \varphi _{1}}\mathbf {Z_{4}} e^{\mathrm {j} \varphi _{4}}=\mathbf {Z_{2}} e^{\mathrm {j} \varphi _{2}}\mathbf {Z_{3}} e^{\mathrm {j} \varphi _{3}}}$

${\displaystyle \mathbf {Z_{1}} \mathbf {Z_{4}} e^{\mathrm {j} (\varphi _{1}+\varphi _{4})}=\mathbf {Z_{2}} \mathbf {Z_{3}} e^{\mathrm {j} (\varphi _{2}+\varphi _{3})}}$

Když tuto rovnici rozdělíme na dvě skalární, dostaneme dvě podmínky rovnováhy.

${\displaystyle |\mathbf {Z_{1}} ||\mathbf {Z_{4}} |=|\mathbf {Z_{2}} ||\mathbf {Z_{3}} |}$

${\displaystyle \ \varphi _{1}+\varphi _{4}=\varphi _{2}+\varphi _{3}}$

Číslicové měřiče impedancí

Číslicové měřiče impedancí mohou pracovat na různých principech, často se využívá převodník impedance-napětí nebo převodník admitance-napětí s využitím operačních zesilovačů.

Impedance a norma

S impedancí se lze také setkat při posuzování bezpečnosti elektrických instalací NN (například při revizích). Podmínky pro impedanci sítě TN (běžný druh sítě, nejčastěji používaný, např. i v bytových instalacích), stanoví ČSN 33 2000-4-41 ed.2 v článku 411.4.4. (dříve stará, dnes již neplatná ČSN 33 2000-4-41 v článku 413.1.3.3). Velikost impedance sítě TN určuje bezpečnost instalace tím, že je směrodatná pro rychlost vypnutí předřazeného jisticího přístroje (pojistka, jistič apod.). Aby jistící přístroj vypnul při poruše v dostatečně krátkém čase, musí být impedance dostatečně nízká. Podrobněji viz výše uvedená ČSN.

Odkazy

Literatura

• SEDLÁK, Bedřich; ŠTOLL, Ivan. Elektřina a magnetismus. 2., opravené a rozšíření vyd. Praha: Academia, 2002. 632 s. ISBN 80-200-1004-1. 

• BLAHOVEC, Antonín. Elektrotechnika II. 4., nezměněné vyd. Praha: Informatorium, 2003. 156 s. ISBN 80-7333-013-X. 

• DOLEČEK, Jaroslav. Moderní učebnice elektroniky. Praha: nakladatelství BEN - technická literatura, 2005. 344 s. ISBN 80-7300-146-2. 

• Elektrotechnická měření. 1. vyd. Praha: nakladatelství BEN - technická literatura, 2002. 256 s. ISBN 80-7300-022-9. 

Související články

• Admitance
• Reaktance
• Rezistance

Externí odkazy

• Sériový RLC obvod (slovensky)
• Měření impedance (česky)
• Popis impedance (anglicky)
• Užití impedance (anglicky)

Autoritní data	PSH: 2514 GND: 4128475-6 LCCN: sh85064610 NDL: 00564146 NLI: 987007541087005171