Osmnáctiúhelník

Pravidelný osmnáctiúhelník a jeho úhly

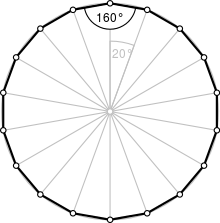
Osmnáctiúhleník, cizím slovem octadecagon či octakaidecagon (z řec. δεκαοχτώ, dekaochtó – osmnáct, a γωνία, gonia – úhel), je mnohoúhelník s osmnácti stranami a vrcholy.

Popis pravidelného osmnáctiúhelníku

Součet středových úhlů pravidelného osmanáctiúhleníku je 360°, jeden středový úhel je tedy ${\displaystyle {\frac {360^{\circ }}{18}}=20^{\circ }}$, což je i hodnota každého vnějšího úhlu.

Jeden vnitřní úhel je ${\displaystyle 180^{\circ }-20^{\circ }}$, součet všech vnitřních úhlů je tedy ${\displaystyle 160^{\circ }\cdot 18=2880^{\circ }}$.

Je-li α délka strany, pak:

• obvod: ${\displaystyle P=18\,a}$
• obsah: ${\displaystyle A={\frac {18}{4}}\,a^{2}\cot \left({\frac {\pi }{18}}\right)}$

  

  Pravidelný osmnáctiúhelník se všemi možnými spojnicemi vrcholů

• minimální poloměr: ${\displaystyle H={\frac {2\,A}{P}}={\frac {a}{2}}\cot \left({\frac {\pi }{18}}\right)}$
• maximální poloměr: ${\displaystyle R={\frac {H}{\cos \left({\frac {\pi }{18}}\right)}}={\frac {a}{2\sin \left({\frac {\pi }{18}}\right)}}}$

Rýsování

Rýsování pravidelného osmnáctiúhelníku

Pravidelný osmnáctiúhelník nelze narýsovat pouze za pomoci pravítka a kružítka, neboť aby bylo možno daný pravidelný mnohoúhelník narýsovat, musí být všechny jeho liché dělitele být Fermatova čísla (${\displaystyle F_{n}=2^{2^{\overset {n}{}}}+1}$).

Osmnáct je dělitelné devíti, což je liché číslo a přitom není Fermanovo. S menší odchylkou (středový úhel se změní z  ${\displaystyle 20^{\circ }}$ na ${\displaystyle 19,99953^{\circ }}$, odchylka tedy ${\displaystyle 0,00047^{\circ }}$ a celkově ${\displaystyle 0,00846^{\circ }}$) jej však lze zkonstruovat v 19 krocích:

1. Utvoříme přímku p.
2. Narýsujeme kružnici k se středem I, jež se nalézá na přímce p.
3. Vytvoříme kružnici l se středem v pravém průsečíku kružnice k a přímky p ${\displaystyle J=k\cap p}$, jejíž poloměr je shodný s průměrem kružnice k.
4. Vytvoříme kružnici m se středem v levém průsečíku kružnice k a přímky p ${\displaystyle K=k\cap p}$, jejíž poloměr je shodný s průměrem kružnice k.
5. Narýsujeme přímku q, jež protíná průsečíky kružnic l a m ${\displaystyle L=l\cap m}$ a ${\displaystyle M=l\cap m}$.
6. Narýsujeme kružnici n, jejíž střed se nachází v průsečíku kružnice k a přímky q ${\displaystyle N=k\cap q}$, jejíž průměr je shodný s průměrem kružnice k.
7. Narýsujeme přímku r, jež protíná průsečíky kružnice k s kružnicí n ${\displaystyle O=k\cap n}$ a ${\displaystyle P=k\cap n}$ a je kolmá na přímku p.
8. Zkonstruujeme kružnici o, jejímž středem je průsečík J a jejíž průměr je totožný s průměrem kružnice k.
9. Narýsujeme přímku s, jež je kolmá na průsečík J.
10. Utvoříme kružnici p, která má střed v průsečíku N a průměr totožný s poloměrem kružnice k.
11. Sestrojíme kružnici q, jejíž střed leží v průsečíku kružnice o a přímky s ${\displaystyle R=o\cap s}$ a jejíž průměr je stejný jako poloměr kružnice k.
12. Narýsujeme přímku t, jež je kolmá na přímku q v horním průsečíku kružnice p a přímky q ${\displaystyle S=p\cap q}$. Zároveň ji lze popsat jako přímku, jež protíná průsečík S a horní průsečík přímky s a kružnice p.
13. Narýsujeme přímku u, která protíná bod I a průsečík kružnice n a přímky s ${\displaystyle T=n\cap s}$.
14. Sestrojíme kružnici r, která má střed v průsečíku J a prochází průsečíkem přímky u a kružnice k ${\displaystyle U=s\cap k}$.
15. Vytvoříme přímku v, která prochází oběma průsečíky kružnice r s kružnicí k a je tak kolmá na přímku p.
16. Zkonstruujeme přímku w, která prochází bodem I a průsečíkem přímky r a v ${\displaystyle V=r\cap v}$.
17. Narýsujeme přímku x, která prochází průsečíkem J a průsečíkem přímky w a t ${\displaystyle W=w\cap t}$.
18. Sestrojíme přímku y, jež prochází bodem I a průsečíkem přímek r a x ${\displaystyle X=r\cap x}$.
19. Přímky p a y svírají úhel α. Vezmeme do kružítka vzdálenost mezi jejich průsečíky s kružnicí k ${\displaystyle Y=p\cap k}$ a ${\displaystyle Z=y\cap k}$ a po obvodu kružnice k si uděláme značky, jež následně spojíme.

Při tomto rýsování vytvoříme množství kružnic, průsečíků a přímek. Zde je jejich přehled:

• Kružnice: k, l, m, n, o, p, q, r
• Průsečíky a body: I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, Y, Z
• Přímky: p, q, r, s, t, u, v, w, x, y

Zajímavosti

Obr. 1

Trojúhelník R_A-Q_A-C_B

Pravidelný trojúhelník A18-A17-B3

Zajímavostí je, že pokud k sobě přitiskneme pravidelný osmnáctiúhelník Α a pravidelný devítiúhelník Β (se stejně dlouhými stranami) body A_A a A_B a R_A a B_B a spojíme úsečkou body Q_A a C_B (vrcholu se pojmenovávají proti směru hodinových ručiček), pak vznikne pravidelný rovnostranný trojúhelník R_A-Q_A-C_B.

Obr. 2

Součet vnějšího úhlu A a vnějšího úhlu B musí být 60° (vnitřní úhel pravidelného trojúhelníku). Vnější úhel α je 20°, vnější úhel β tedy musí být ${\displaystyle \beta =60^{\circ }-20^{\circ }=40^{\circ }}$. Dává to smysl, neboť osmnáctiúhelník má dvakrát více vrcholů a stran než devítiúhelník.

Osmnáctiúhelníky, devítiúhelníky, kosočtverce a trojúhelníky

Osmnáctiúhelníková síť

S pomocí osmnáctiúhelníků, devítiúhelníků, kosočtverců a trojúhelníků v poměru 1:2:8:2 lze sestrojit vzor opakujících se geometrických útvarů. Zde se uplatní předešlý popsaný jev.

Obr. 3

Osmnáctiúhelník vyplněný kosočtverci

Pravidelný osmnáctiúhelník lze několika způsoby vyplnit různě velkými kosočtverci, které však obvykle mají stejnou délku strany a často jich je 36, od každého druhu devět.

Reference

V tomto článku byl použit překlad textu z článku Octadécagone na francouzské Wikipedii.

Externí odkazy