Penroseovo dláždění

Příklad Penroseova dláždění

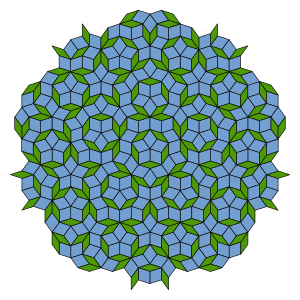
Penroseovo dláždění (anebo také Penroseho pokrytí) je neperiodické dláždění roviny, generované pomocí konečné množiny základních typů dlaždic. Neperiodický znamená, že není invariantní vůči žádnému posunutí, tj. žádné posunutí nezobrazí dláždění na sebe sama. Dláždění bylo pojmenováno po anglickém matematikovi a fyzikovi jménem Roger Penrose, který se touto problematikou zabýval v 70. letech 20. století. Penroseovo dláždění může být zkonstruováno tak, aby bylo osově souměrné i invariantní vůči otočení kolem jednoho bodu, jako na obrázku.

Vlastnosti

Penroseovo dláždění má mnoho pozoruhodných vlastností, zejména:

• je neperiodické, neformálně řečeno posunutá kopie nebude nikdy odpovídat originálu,
• je soběpodobné, stejné vzory se objevují ve větším měřítku,
• každá konečná část se vyskytne v dláždění nekonečně-krát
• pokud se z dláždění realizuje fyzická struktura, jedná se o kvazikrystal.

Příklad

Nejjednodušší Penroseho pokrytí je možné zkonstruovat z dvou typů kosočtverců,^[1] které je znázorněno na obrázku. Toto pokrytí je symetrické vůči rotaci kolem jednoho bodu o pětinu kruhu a poměr četností větších a menších kosočtverců je stejně jako poměr jejich obsahů roven zlatému řezu.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Penrose tiling na anglické Wikipedii.

1. L. Motl, M. Zahradnik, Pěstujeme lineární algebru (Penroseho pokrytí) Archivováno 16. 9. 2011 na Wayback Machine.

Související články

• Fraktál
• Kvazikrystal
• L-systém
• Teorie centrálních míst

Externí odkazy

• Penroseovo dláždění v encyklopedii MathWorld