Penterakt
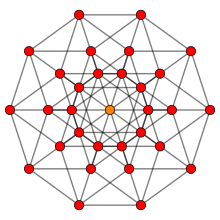
V geometrii je penterakt pětirozměrnou analogií krychle, jde tedy o speciální variantu nadkrychle pro d=5. Odborněji by mohl být penterakt definován jako pravidelný konvexní čtyřúhelník s deseti teseraktovými nadstěnami a čtyřiceti krychlovými stěnami.
Objem a obsah penteraktu
[editovat | editovat zdroj]Tyto vzorce uvádějí obsah penteraktu a jeho k-rozměrné povrchy.
V=a5
S4D=10 a4
S3D=40 a3
S2D=80 a2
S1D=80 a
| VÍCEROZMĚRNÁ GEOMETRICKÁ TĚLESA | ||||
|---|---|---|---|---|
| d=2 | trojúhelník | čtverec | pětiúhelník | šestiúhelník |
| d=3 | jehlan | krychle | dvanáctistěn,dvacetistěn | |
| d=4 | 5nadstěn | teserakt | 24nadstěn | 120nadstěn,600nadstěn |
| d=5 | 5simplex | penterakt | ||
| d=6 | 6simplex | hexerakt | ||
| d=7 | 7simplex | hepterakt | ||
| d=8 | 8simplex | okterakt | ||
| d=9 | 9simplex | ennerakt | ||
| d=10 | 10simplex | dekerakt | ||
| d=11 | 11simplex | hendekerakt | ||
| d=12 | 12simplex | dodekerakt | ||
| d=13 | 13simplex | triskaidekerakt | ||
| d=14 | 14simplex | tetradekerakt | ||
| d=15 | 15simplex | pentadekerakt | ||
| d=16 | 16simplex | hexadekerakt | ||
| d=17 | 17simplex | heptadekerakt | ||
| d=18 | 18simplex | oktadekerakt | ||
| d=19 | 19simplex | ennedekerakt | ||
| d=20 | 20simplex | ikosarakt | ||
| d=21 | 21simplex | henikosarakt | ||
| d=22 | 22simplex | doikosarakt | ||
| d=23 | 23simplex | triskaiikosarakt | ||
| d=24 | 24simplex | tetraikosarakt | ||
| d=25 | 25simplex | pentaikosarakt | ||
| d=26 | 26simplex | hexaikosarakt |
Externí odkazy
[editovat | editovat zdroj] Obrázky, zvuky či videa k tématu Penterakt na Wikimedia Commons
Obrázky, zvuky či videa k tématu Penterakt na Wikimedia Commons