Rovnoběžnostěn

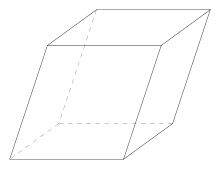
Rovnoběžnostěn

Rovnoběžnostěn je čtyřboký hranol, jehož podstavou je rovnoběžník. Mezi rovnoběžnostěny patří např. kvádr, krychle nebo klenec.

Povrch

Povrch rovnoběžnostěnu je tvořen součtem obsahů šesti rovnoběžníků, z nichž každé dva protilehlé jsou shodné. Užitím vzorce pro výpočet obsahu rovnoběžníku v trojrozměrném prostoru dostáváme

${\displaystyle P=2{\Bigg [}{\Big (}(\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {a} \times \mathbf {b} ){\Big )}^{1/2}+{\Big (}(\mathbf {b} \times \mathbf {c} )\cdot (\mathbf {b} \times \mathbf {c} ){\Big )}^{1/2}+{\Big (}(\mathbf {c} \times \mathbf {a} )\cdot (\mathbf {c} \times \mathbf {a} ){\Big )}^{1/2}{\Bigg ]}}$

kde ${\displaystyle \mathbf {a} ,\,\mathbf {b} ,\,\mathbf {c} }$ jsou tři různoběžné stranové vektory, "${\displaystyle \times }$" značí vektorový součin dvou vektorů a "${\displaystyle \,\cdot \,}$" značí skalární součin dvou vektorů.

Zobecněním vektorového součinu do ${\displaystyle n}$-rozměrného prostoru (jedná se o součin ${\displaystyle (n-1)}$ lineárně nezávislých vektorů délky ${\displaystyle n}$, jehož výsledkem je vektor kolmý na všechny předchozí, tvořící s nimi, v daném pořadí, pravotočivou bázi) lze zcela analogicky spočítat ${\displaystyle (n-1)}$-rozměrný nadpovrch libovolného ${\displaystyle n}$-rozměrného nadrovnoběžnostěnu.

Objem

Objem rovnoběžnostěnu je roven absolutní hodnotě smíšeného součinu (tří různoběžných) stranových vektorů

${\displaystyle V=\left|(\mathbf {a} \times \mathbf {b} )\cdot \mathbf {c} \right|=\left|(\mathbf {b} \times \mathbf {c} )\cdot \mathbf {a} \right|=\left|(\mathbf {c} \times \mathbf {a} )\cdot \mathbf {b} \right|.}$

Pokud jsou vrcholy ${\displaystyle A,B,C,D,E,F,G,H}$ rovnoběžnostěnu zadány pomocí souřadnic v prostoru, tj. ${\displaystyle A=(x_{A},y_{A},z_{A})}$, ${\displaystyle B=(x_{B},y_{B},z_{B})}$ atd., lze objem rovnoběžnostěnu vyjádřit po složkách. Je roven absolutní hodnotě determinantu sestaveného ze souřadnic libovolných čtyř vrcholů neležících v jedné rovině takto

${\displaystyle V=\left|\det \left({\begin{array}{ccc}x_{D}-x_{A}&x_{B}-x_{A}&x_{E}-x_{A}\\y_{D}-y_{A}&y_{B}-y_{A}&y_{E}-y_{A}\\z_{D}-z_{A}&z_{B}-z_{A}&z_{E}-z_{A}\end{array}}\right)\right|.}$

Ztotožníme-li, pro jednoduchost, vrchol ${\displaystyle A}$ s počátkem souřadného systému, tj. ${\displaystyle A=(0,0,0)}$, pak tedy

${\displaystyle V=|x_{D}y_{B}z_{E}+x_{B}y_{E}z_{D}+x_{E}y_{D}z_{B}-x_{D}y_{E}z_{B}-x_{B}y_{D}z_{E}-x_{E}y_{B}z_{D}|.}$

Zcela analogicky lze spočítat obsah libovolného rovnoběžníku, resp. nadobjem libovoného ${\displaystyle n}$-rozměrného nadrovnoběžnostěnu.

Související články

• Hranol
• Rovnoběžník

Externí odkazy