Smíšený součin

Smíšený součin^[1] je v matematice operace násobení vektorů v trojrozměrném vektorovém prostoru se skalárním součinem, kterou lze definovat jako skalární součin prvního vektoru s vektorovým součinem druhého a třetího vektoru.

Definice

Mějme aritmetický vektorový prostor ${\displaystyle \mathbb {R} ^{3}}$ s kanonickou bází nad číselným tělesem ${\displaystyle \mathbb {R} }$, pak vektory ${\displaystyle \mathbf {a} ,\mathbf {b} ,\mathbf {c} \in \mathbb {R} ^{3}}$ v daném pořadí tvoří smíšený součin, platí-li:

${\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=det[\mathbf {a} ,\mathbf {b} ,\mathbf {c} ]={\begin{vmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{vmatrix}}=a_{1}b_{2}c_{3}-a_{1}b_{3}c_{2}+a_{2}b_{3}c_{1}-a_{2}b_{1}c_{3}+a_{3}b_{1}c_{2}-a_{3}b_{2}c_{1}}$,

kde ${\displaystyle a_{i},b_{i},c_{i}}$ pro ${\displaystyle i\in \{1,2,3\}}$ jsou složky vektorů ${\displaystyle \mathbf {a} ,\mathbf {b} ,\mathbf {c} }$.

Vlastnosti

Objem rovnoběžnostěnu je absolutní hodnotou determinantu vektorů ${\displaystyle r_{1}}$, ${\displaystyle r_{2}}$ a ${\displaystyle r_{3}}$.

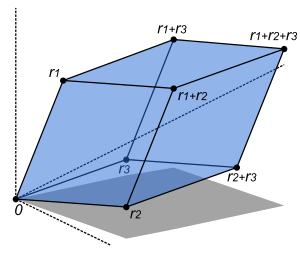
• Geometrický význam smíšeného součinu je objem rovnoběžnostěnu jimi určeného.
• Při záměně libovolných dvou vektorů ve smíšeném součinu zůstává absolutní hodnota výsledku stejná, výsledek ale změní znaménko, tj. výsledek smíšeného součinu závisí na pořadí vektorů.
• Vektorový součin kolineárních vektorů je nulový vektor, tj. smíšený součin je pak roven nule.
• Smíšený součin vektorů kladně orientované kanonické báze je roven jedné.
• Smíšený součin je jednotková antisymetrická trilineární forma, lze jej vyjádřit pomocí Levi-Civitova symbolu ${\displaystyle \varepsilon }$ s Einsteinovou sumační konvencí: ${\displaystyle [\mathbf {a} ,\mathbf {b} ,\mathbf {c} ]=\varepsilon _{ijk}a_{i}b_{j}c_{k}}$.

Reference

1. BICAN, Ladislav. Linearni algebra a geometrie (upr. vydání). [s.l.]: Academia, 2009. ISBN 978-80-200-1707-9. Je zde použita šablona {{Citation}} označená jako k „pouze dočasnému použití“.

Související články

• Vektorový prostor
• Skalární součin
• Vektorový součin