Theorem gwerth-cymedrig

Ar gyfer unrhyw ffwythiant sy'n ddi-dor ar ${\displaystyle [a,b]}$ ac yn ddifferadwy ar ${\displaystyle (a,b)}$ mae yna ryw ${\displaystyle c}$ yn y cyfwng ${\displaystyle (a,b)}$ fel bod y secant sy'n ymuno pwyntiau terfyn y cyfwng ${\displaystyle [a,b]}$ yn baralel i'r tangiad yn ${\displaystyle c}$.

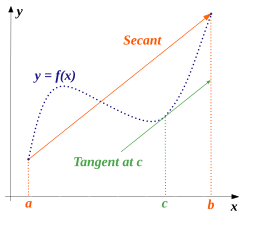
Mewn mathemateg, mae'r theorem gwerth-cymedrig yn nodi, yn fras, os rhoddir arc blanar rhwng dau bwynt terfyn, bodolir o leiaf un pwynt lle mae'r tangiad i'r arc yn baralel i'r secant trwy ei bwyntiau terfyn.

Yn fanwl gywir, os yw ${\displaystyle f}$ yn ffwythiant di-dor ar gyfwng caeedig${\displaystyle [a,b]}$, ac yn ddifferadwy ar y cyfwng agored ${\displaystyle (a,b)}$, yna mae pwynt ${\displaystyle c}$ yn bodoli o fewn ${\displaystyle (a,b)}$ fel bod y tangiad yn c yn baralel i'r llinell secant trwy'r pwyntiau terfyn ${\displaystyle (a,f(a))}$ ac ${\displaystyle (b,f(b))}$, hynny yw,

${\displaystyle f'(c)={\frac {f(b)-f(a)}{b-a}}.}$

Mae'n un o'r canlyniadau pwysicaf mewn dadansoddiad real.

Hanes

Disgrifiwyd achos arbennig o’r theorem hon yn gyntaf gan Parameshvara (1370–1460), o Ysgol Seryddiaeth a Mathemateg Kerala yn India, yn ei sylwebaethau ar Govindasvāmi a Bhāskara II.^[1] Profwyd ffurf gyfyngedig o'r theorem gan Michel Rolle ym 1691; y canlyniad oedd yr hyn a elwir bellach yn theorem Rolle, ac fe'i profwyd ar gyfer polynomialau yn unig, heb dechnegau calcwlws. Cafodd y theorem gwerth-cymedrig yn ei ffurf fodern ei nodi a'i brofi gan Augustin Louis Cauchy ym 1823.^[2]

Datganiad ffurfiol

Mae'r ffwythiant ${\displaystyle f}$ yn cyflawni graddiant y secant rhwng ${\displaystyle a}$ a ${\displaystyle b}$ fel ei deilliad ar y pwynt ${\displaystyle \xi \in (a,b)}$.

Mae hefyd yn bosibl bod mwy nag un tangiad yn baralel i'r secant.

Gadewch i${\displaystyle f:[a,b]\to \mathbb {R} }$ bod yn ffwythiant di-dor ar y cyfwng caeedig ${\displaystyle [a,b]}$, ac yn ddifferadwy ar y cyfwng agored ${\displaystyle (a,b)}$, lle${\displaystyle a<b}$. Yna bodolir rhyw ${\displaystyle c}$ o fewn ${\displaystyle (a,b)}$ fel bod

${\displaystyle f'(c)={\frac {f(b)-f(a)}{b-a}}.}$

Mae'r theorem gwerth-cymedrig yn cyffredinoli theorem Rolle, sydd â'r dybiaeth bod ${\displaystyle f(a)=f(b)}$, hynny yw bod ochr dde'r mynegiant uchod yn sero.

Mae'r theorem gwerth-cymedrig yn dal i fod yn ddilys mewn lleoliad ychydig yn fwy cyffredinol. Nid oes ond angen tybio hynny${\displaystyle f:[a,b]\to \mathbb {R} }$ yn barhaus ar${\displaystyle [a,b]}$, a hynny am bob ${\displaystyle x}$ yn${\displaystyle (a,b)}$ y terfyn

Mae'r mynegiant ${\displaystyle {\frac {f(b)-f(a)}{(b-a)}}}$ yn rhoi graddiant y llinell sy'n ymuno'r pwyntiau ${\displaystyle (a,f(a))}$ ac ${\displaystyle (b,f(b))}$, sy'n gord i graff ${\displaystyle f}$. Mae${\displaystyle f'(x)}$ yn rhoi graddiant y tangiad i'r gromlin yn y pwynt ${\displaystyle (x,f(x))}$. Felly mae'r theorem gwerth-cymedrig yn dweud, o ystyried unrhyw gord cromlin esmwyth, y gallwn ddod o hyd i bwynt sy'n gorwedd rhwng diweddbwyntiau'r cord fel bod y tangiad ar y pwynt hwnnw yn baralel i'r cord.

Prawf

Diffiniwch ${\displaystyle g(x)=f(x)-rx}$, lle mae ${\displaystyle r}$ yn gysonyn. Gan fod ${\displaystyle f}$ yn ddi-dor ar ${\displaystyle [a,b]}$ ac yn ddifferadwy ar ${\displaystyle (a,b)}$, mae'r un peth yn wir am ${\displaystyle g}$. Rydyn ni nawr eisiau dewis ${\displaystyle r}$ fel bod ${\displaystyle g}$ yn bodloni amodau theorem Rolle, sef

O theorem Rolle, gan fod ${\displaystyle g}$ yn ddifferadwy ac mae ${\displaystyle g(a)=g(b)}$, mae yna bodoler rhyw ${\displaystyle c}$ o fewn ${\displaystyle (a,b)}$ lle mae ${\displaystyle g'(c)=0}$. Mae'n dilyn o'r hafaliad ${\displaystyle g(x)=f(x)-rx}$ bod,

${\displaystyle {\begin{aligned}&g'(x)=f'(x)-r\\&g'(c)=0\\&g'(c)=f'(c)-r=0\\&\Rightarrow f'(c)=r={\frac {f(b)-f(a)}{b-a}}\end{aligned}}}$

Cyfeiriadau

1. J. J. O'Connor and E. F. Robertson (2000). Paramesvara Archifwyd 2015-04-02 yn y Peiriant Wayback, MacTutor History of Mathematics archive.
2. Ádám Besenyei. "Historical development of the mean value theorem" (PDF).