Middelværdisætningen
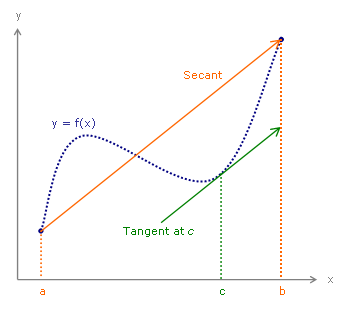
Middelværdisætningen er en matematisk sætning, der, i grove træk, siger, at der et sted på en differentiabel kurve er et punkt, i hvilket hældningen er lig kurvens "gennemsnitshældning".
Sætningen kan illustreres med et konkret eksempel; en bils hastighed. Hvis en bil på en strækning har kørt 80km/t i gennemsnit, har den mindst ét sted på strækningen kørt præcis 80km/t.
Sætningen blev først udviklet af inderen Parameshvara (1370 – 1460) og senere af Lagrange (1736 – 1813). Den er infinitesimalregningens vigtigste resultat, og er en central del af beviset for infinitesimalregningens hovedsætning. Sætningen benyttes sjældent til egentlige matematiske udregninger, men oftere som del af beviser for andre matematiske sætninger.
Formel definition
[redigér | rediger kildetekst]Lad være en funktion, der er kontinuert på det lukkede interval og differentiabel på det åbne interval . Da eksisterer et , så
Middelværdisætningen er et mere generelt tilfælde af Rolles sætning, der antager at .
Middelværdisætningen kan generaliseres yderligere, idet det er nok at antage, at er kontinuert på , og at grænseværdien er et reelt tal eller for alle .
Bevis
[redigér | rediger kildetekst]Sekanten på illustrationen kan som bekendt gives ved en ligning , hvor , og det er muligt at lave en funktion
- ,
så der gælder, at er kontinuert på og differentiabel på . Samtidig gælder og , og så opfylder antagelsene for Rolles sætning, så der eksisterer et , så . Men
- ,
og sætningen er vist. Q.E.D.
Cauchys middelværdisætning
[redigér | rediger kildetekst]Cauchys middelværdisætning er en matematisk sætning af Augustin Louis Cauchy. Den er også kendt under navnet den udvidede middelværdisætning, og er en mere generel variant af den traditionelle middelværdisætning. Den benyttes blandt andet som hjælpemiddel i et klassisk bevis for l'Hôpitals regel.
Sætningen
[redigér | rediger kildetekst]Hvis to funktioner, og , er kontinuerte på deres definitionsmængde, , og differentiable på det åbne interval , eksisterer et , så
.
Et bevis for sætningen
[redigér | rediger kildetekst]Et simpelt bevis for sætningen, der minder meget om det typisk anvendte bevis for middelværdisætningen, går på at finde en funktion, der opfylder Rolles sætning. Hvis er defineret ved:
er den tydeligvis kontinuert på og differentiabel på med differentialkvotienten
.
Idet og , opfylder antagelserne i Rolles sætning, og der eksisterer således et , så
,
hvilket kan omskrives til udsagnet i sætningen. Q.E.D. Det ses også, at sætningen også gælder, når brøkens nævner er 0, men typisk anvendes den anden skrivemåde, da denne er lettere at huske, samtidig med at det typisk er den, man har behov for.
![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle ]a,b[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b51ec208e9582e11a4f340a42d4f17fb4748fcb)
![{\displaystyle c\in ]a,b[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a1a9da539d0c4ae16894e231068b7adbd568c66)




![{\displaystyle x\in ]a,b[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/908b0e913219e22a7853e1b09ecfb095a50b59e9)









![{\displaystyle g:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b1d5103d0e36767a27715bcfc57137119294aad)



