Algorithmus von Ford und Fulkerson
Der Algorithmus von Ford und Fulkerson ist ein Algorithmus aus dem mathematischen Teilgebiet der Graphentheorie zur Bestimmung eines maximalen Flusses in einem Flussnetzwerk mit rationalen Kapazitäten. Er wurde nach seinen Erfindern L.R. Ford Jr. und D.R. Fulkerson benannt.[1] Die Anzahl der benötigten Operationen hängt vom Wert des maximalen Flusses ab und ist im Allgemeinen nicht polynomiell beschränkt. Weiterentwicklungen führten zum Algorithmus von Edmonds und Karp und dem Algorithmus von Dinic.
Wirkungsprinzip
[Bearbeiten | Quelltext bearbeiten]Der Algorithmus beruht auf der Idee, einen Weg von der Quelle zur Senke zu finden, entlang dessen der Fluss weiter vergrößert werden kann, ohne die Kapazitätsbeschränkungen der Kanten zu verletzen. Ein solcher Weg wird auch als augmentierender Pfad bezeichnet. Durch Wiederholung können die Flüsse entlang mehrerer solcher Wege zu einem noch größeren Gesamt-Fluss zusammengefasst werden. Wird stets der kürzeste Weg gewählt, ergibt sich der Edmonds-Karp-Algorithmus.
Damit auf diese Weise tatsächlich stets der maximale Fluss gefunden werden kann, muss auch zugelassen werden, dass der Weg Kanten des Netzwerkes in umgekehrter Richtung folgt und für diese Kanten den Fluss wieder reduziert (sog. Rückkanten, s. u.). In der Analogie einer realen Flüssigkeitsbewegung bspw. durch ein Rohrleitungs-Netzwerk entspricht das der Idee, dass man anstatt einen Teil der durch eine Leitung fließenden Flüssigkeit wieder zurückzuschicken auch einfach von vornherein eine entsprechende Menge weniger durch diese Leitung schicken kann.
Formale Beschreibung
[Bearbeiten | Quelltext bearbeiten]Gegeben sei ein Netzwerk , bestehend aus einem endlichen, gerichteten Graphen mit einer Quelle , einer Senke und einer Kapazitätsfunktion , die jeder Kante eine nichtnegative reelle Zahl als Kapazität zuordnet.
Der Algorithmus verändert in jedem Durchlauf einen s-t-Fluss im Netzwerk , also eine Abbildung mit den Eigenschaften
- Kapazitätsbeschränkung: Für jede Kante ist der Fluss durch beschränkt.
- Flusserhaltung: Für jeden Knoten gilt:
- .
Hierbei bezeichnet die Menge der aus hinausführenden Kanten und die Menge der in hineinführenden Kanten. Der in einen Knoten eingehende Fluss muss also gleich dem ausgehenden Fluss sein.
Der Algorithmus sucht in jedem Schritt einen Weg von nach im Residualgraphen. Der Residualgraph teilt sich mit dieselbe Knotenmenge und enthält die Kanten von , die von nicht ausgelastet sind, ergänzt um sogenannte Rückkanten: Für jede Kante mit enthält jeweils zusätzlich eine Rückkante . Formal gilt also: Dazu werden Residualkapazitäten definiert, die jeder Kante zuordnen, um wie viel der Fluss auf noch erhöht werden kann, und jeder Rückkante zuordnen, um wie viel der Fluss auf der zugehörigen Hinkante verringert werden kann. Also formal:
Zur Initialisierung kann ein beliebiger Fluss verwendet werden (auch der Nullfluss, der jeder Kante den Wert 0 zuordnet). Der Algorithmus beschreibt sich wie folgt:
- (Initialisierung mit Nullfluss:) Setze für jede Kante .
- Solange es im Residualgraphen einen Weg von nach gibt, bestimme einen solchen Weg und tue:
- Bestimme .
- Für alle setze: .
- Für alle setze für die zugehörige Hinkante : .
Sind alle Kapazitäten rational, berechnet der Algorithmus nach endlich vielen Schritten einen maximalen s-t-Fluss.
Beispiel
[Bearbeiten | Quelltext bearbeiten]| Beschreibung | Graph (mit Kapazitäten ) |
Fluss | Residualgraph (mit Residual-Kapazitäten ) | ||||||||||||||||||||||||||||||||||||||||||
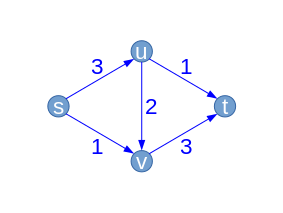
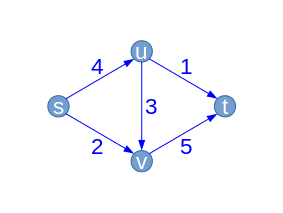
| Wir betrachten das s-t-Flussnetzwerk , bestehend aus dem Graphen mit vier Knoten und fünf Kanten , der Quelle , der Senke und der rechts angegebenen Kapazitätsfunktion .
Wir starten mit dem leeren Fluss , der jeder Kante den Wert zuordnet. Damit entspricht der Residualgraph zunächst genau dem Netz und die zugehörigen Residual-Kapazitäten genau den Kapazitäten . |

|
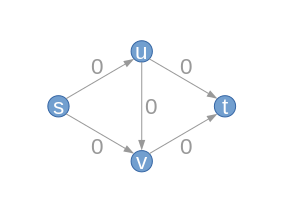
|

| ||||||||||||||||||||||||||||||||||||||||||
| Beschreibung | Augmentierender Pfad (mit Residual-Kapazitäten ) |
Fluss | Residualgraph (mit Residual-Kapazitäten ) | ||||||||||||||||||||||||||||||||||||||||||
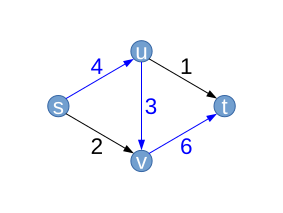
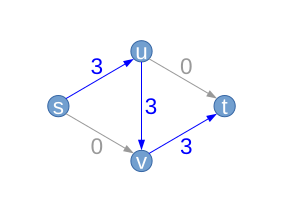
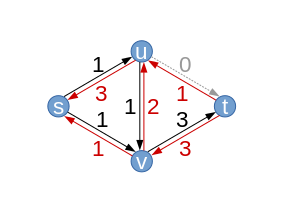
| Nehmen wir an, der Algorithmus wählt als erstes den Pfad , d. h. (blau). Entlang dieses Pfades können wir wegen den Fluss höchstens um erhöhen (die mittlere Kante von oben nach unten). Daraus ergibt sich ein neuer Fluss (wir bezeichnen ihn wieder mit ) mit .
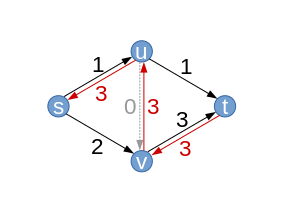
Die Kante hat eine Kapazität von , wir nutzen davon im Moment jedoch nur . Im Residualgraphen bleibt die Kante daher mit einer Residualkapazität von erhalten. Anders ist das beispielsweise mit der Kante , bei der keine Residualkapazität übrig bleibt. Sie „verschwindet“ deshalb aus dem Residualgraphen (grau gestrichelt dargestellt). Für die Kante ergibt sich eine Residualkapazität von . Weiterhin haben wir jetzt drei Kanten mit einem Fluss größer als Null. Diesen Fluss können wir theoretisch auch wieder „zurückschicken“, weshalb wir drei neue „Rückwärtskanten“ einführen, deren Residualkapazität genau dem aktuellen Fluss zwischen den beiden Knoten entspricht (rot). |
|
|
| ||||||||||||||||||||||||||||||||||||||||||
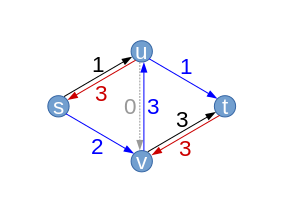
| Gehen wir davon aus, der Algorithmus wählt im nächsten Schritt den Pfad . Die maximale Flussvergrößerung entlang dieses Pfades ergibt sich aus der Residualkapazität der Kante . Dabei nutzen wir erstmals eine Rückwärtskante, die Kante . Während sich der Fluss f entlang der Kanten sv und ut um 1 erhöht, verringert sich der Fluss hingegen entlang der Kante uv um 1 von 3 auf 2. Damit ist die Kapazität dieser Kante nicht länger ausgenutzt, und die Kante uv kehrt in den Residualgraphen zurück, dieses Mal mit der Residualkapazität . Dafür „verschwindet“ dieses Mal ut. Die Residualkapazität von sv verringert sich um 1 auf 1.
Man beachte: alle Rückwärtskanten im Residualgraph haben wieder dieselbe Residualkapazität, die dem Wert des Flusses zwischen ihren beiden Knoten entspricht. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||
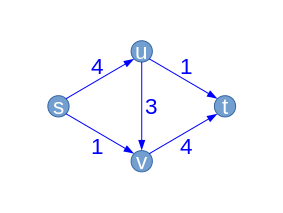
| Als nächstes finde der Algorithmus z. B. erneut . Dieses Mal lässt sich der Fluss entlang dieses Pfades lediglich noch um 1 erhöhen, gerade den Betrag, den wir im vorigen Schritt entlang der Kante uv wieder zurückgeschickt haben. Man merkt hier schon, dass der Algorithmus unter Umständen viel „hin und her“ schiebt, mehr dazu unter Laufzeit. | 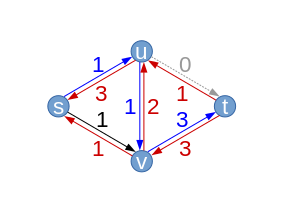
|
|

| ||||||||||||||||||||||||||||||||||||||||||
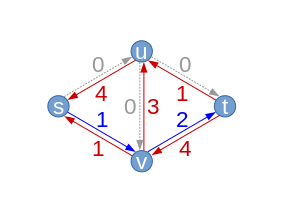
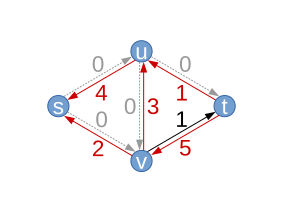
| Im letzten Schritt kann nur noch der Pfad gefunden werden. Dieser erhöht den Fluss nochmals um 1, für einen Gesamtwert des Flusses von . Das kann man auch gut daran erkennen, dass die von der Quelle s ausgehenden Kanten zusammen einen Fluss von aufweisen, ebenso wie die in der Senke t endenden Kanten. Dieser Fluss ist tatsächlich maximal, was sich leicht daran erkennen lässt, dass alle Kanten, welche von der Quelle ausgehen, voll ausgelastet sind (diese beiden Kanten sind ein Flaschenhals, d. h. die Schnittkanten eines minimalen Schnitts).
Der Algorithmus terminiert anschließend, da im sich ergebenden Residualgraphen kein Weg von s nach t mehr gefunden werden kann. Würde man den Algorithmus insofern ergänzen, dass er untersucht, welche Knoten von s noch erreichbar sind, ergäbe sich automatisch der o.a. minimale Schnitt, in diesem Fall enthält er lediglich den Knoten s, von dem man keinen anderen mehr erreichen kann (siehe Max-Flow-Min-Cut-Theorem). |
|
|
|
Korrektheit
[Bearbeiten | Quelltext bearbeiten]Ford und Fulkerson konnten beweisen, dass ein s-t-Fluss in einem Netzwerk genau dann maximal ist, wenn es keinen augmentierenden Pfad gibt, d. h., wenn das Restnetzwerk keinen Pfad von nach besitzt. Daher gilt:
- Falls der Algorithmus von Ford und Fulkerson zum Stehen kommt, ist ein maximaler s-t-Fluss gefunden.
Dabei muss der maximale s-t-Fluss nicht eindeutig bestimmt sein.
Bei der Durchführung des Algorithmus vergrößert sich der betrachtete Fluss mit jedem Schritt. Daraus folgt eine wichtige Tatsache für ganzzahlige Netzwerke:
- Sind alle Kapazitäten des gegebenen Netzwerks nichtnegative ganze Zahlen, so kommt der Algorithmus von Ford und Fulkerson nach endlich vielen Schritten zum Stehen und liefert einen maximalen s-t-Fluss, der außerdem ganzzahlig ist.
Sind alle Kapazitäten rationale Zahlen, so erhält man durch Multiplikation mit dem Hauptnenner ein ganzzahliges Netzwerk, und kann so die folgende Aussage beweisen:
- Sind alle Kapazitäten des gegebenen Netzwerks nichtnegative rationale Zahlen, so kommt der Algorithmus von Ford und Fulkerson nach endlich vielen Schritten zum Stehen und liefert einen maximalen s-t-Fluss, der außerdem nur rationale Werte hat.
Falls irrationale Zahlen als Kapazitäten vorkommen, gilt das nicht mehr: Ford und Fulkerson konstruierten ein Beispiel eines Netzwerkes mit 10 Knoten und 48 Kanten, bei dem ihr Algorithmus bei geeigneter Auswahl der augmentierenden Pfade nicht zum Stehen kommt und auch nicht gegen einen maximalen Fluss konvergiert[2]. Im Jahr 1995 fand Uri Zwick ein Beispiel mit 6 Knoten und 8 Kanten und einem derartigen Verhalten[3].
Laufzeit
[Bearbeiten | Quelltext bearbeiten]Der Algorithmus von Ford und Fulkerson findet einen maximalen Fluss (sofern er terminiert) in Rechenschritten (siehe Landau-Notation), wobei die Anzahl der Knoten des Netzwerkes, die Anzahl der Kanten des Netzwerkes, den Wert des maximalen Flusses und den Hauptnenner der Kapazitäten bezeichnen. Sind die Kantengewichte irrational, so kann es auftreten, dass der Algorithmus nicht terminiert[4].

Einerseits benötigt jeder Schleifendurchlauf des Algorithmus lediglich Operationen, aber andererseits hängt die benötigte Anzahl der Schleifendurchläufe von der Größe der Kapazitäten ab. Es ist möglich, die flussvergrößernden Pfade sehr ungünstig zu wählen. Das kann man sich am Beispiel links verdeutlichen: der Algorithmus kann in diesem Beispiel in jedem Schritt einen Weg über die mittlere Kante (ggf. als Rückwärtskante) wählen und den Gesamt-Fluss dadurch nur um 1 erhöhen.
Wählt man in jedem Schritt immer einen kürzesten augmentierenden Pfad zur Vergrößerung des Flusses, so erhält man den Algorithmus von Edmonds und Karp, der stets in Laufzeit einen maximalen s-t-Fluss konstruiert. Eine weitere Verbesserung mit Hilfe zusätzlicher Techniken bringt der Algorithmus von Dinic mit einer (worst-case)-Komplexität von .
Pseudocode
[Bearbeiten | Quelltext bearbeiten]Eingabe: Ursprungsgraph
Ausgabe: Graph mit maximalem Fluss
Berechne Restgraph aus Ursprungsgraph
Solange es einen Erweiterungspfad im Restgraph gibt:
Restkapazität = Minimum( Restkapazität der Kante für jede Kante des Erweiterungspfades )
Für jede Kante des Erweiterungspfades:
Falls Kante in Ursprungsgraph:
Fluss( Kante ) = Fluss( Kante ) + Restkapazität
Sonst:
Fluss( umgekehrte Kante ) = Fluss( umgekehrte Kante ) - Restkapazität
Literatur
[Bearbeiten | Quelltext bearbeiten]- Bernhard Korte, Jens Vygen: Kombinatorische Optimierung: Theorie und Algorithmen. Aus dem Englischen von Rabe von Randow. Springer-Verlag, Berlin Heidelberg 2008, ISBN 978-3-540-76918-7
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Ein kommentierter Quellcode in C ( vom 25. Juni 2005 im Internet Archive) (englisch)
- Web Applet in Java – Algorithmus von Ford und Fulkerson an eigenen Graphen testen (englisch)
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ L.R. Ford Jr., D.R Fulkerson: Maximal flow through a network. In: Canad. J. Math. 8. Jahrgang, 1956, S. 399–404, doi:10.4153/CJM-1956-045-5 (math.ca [PDF]).
- ↑ Lester Randolph Ford junior, Delbert Ray Fulkerson: Flows in Networks, Princeton University Press 1962
- ↑ Uri Zwick: The smallest networks on which the Ford-Fulkerson maximum flow procedure may fail to terminate, Theoretical Computer Science 148, 165–170 (1995).
- ↑ KIT - Fakultät für Informatilk: An Even Worse Example for Ford Fulkerson. In: kit.edu. KIT, 30. Januar 2008, abgerufen am 25. Januar 2022 (englisch).










































































