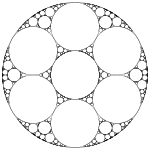
Apollonios-Kreisfüllung

Eine Apollonions-Kreisfüllung, nach dem Vier-Farben-Satz gefärbt

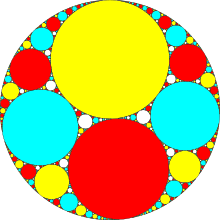
Die Apollonios-Kreisfüllung^{[1]:S. 374f} oder apollonische Kreispackung^[2][3] (englisch apollonian gasket oder apollonian circle packing, ACP) ist in der Geometrie eine Kreispackung, bei der in das Kreisbogendreieck zwischen drei sich paarweise berührenden Kreisen ein weiterer möglichst großer Kreis eingeschrieben und dieser Vorgang rekursiv fortgesetzt wird.

Die Namensgebung rührt vom Berührungsproblem des Apollonios^{[1]:S. 241} her, das Apollonios von Perge formulierte. Das Problem beinhaltet unter anderem die Aufgabe, zu drei gegebenen Kreisen einen vierten zu finden, der die ersten drei berührt. Bei der Füllung berühren sich auch die vorgegebenen Kreise. Die Apollonios-Kreisfüllung ist eines der ersten jemals beschriebenen Fraktale. 2023 konnten zwei Studenten die anerkannte Lokal-Global-Vermutung über sie widerlegen.^[3]

• Apollonios-Kreisfüllungen
• 
  (A) mit Radial­symmetrie
• 
  (B) mit gefüllten Kreisen
• 
  (C) primitiv ganzzahlig
• 
  (D) mit unzutref­fender Lokal-Global-Vermutung

Es gibt Apollonios-Kreisfüllungen, in denen die Kehrwerte der Radien aller Kreise ganzzahlig sind wie in den Abbildungen (C) und (D). Auf diese Weise entsteht eine Verbindung zur Gruppen-^{[4]:S. 2} und Zahlentheorie.^[5]

Definitionen

Folgende Begriffe tauchen im Zusammenhang mit Apollonios-Kreisfüllungen auf:

• Die Krümmungen der Kreise sind die Kehrwerte ihrer Radien.
• Eine ganzzahlige Kreisfüllung (englisch integral packing) enthält ausschließlich Kreise mit ganzzahliger Krümmung.
• Ein Descartes-Quadrupel ist eine Gruppe von vier Zahlen {a,b,c,d}, die eine Lösung der descartschen Gleichung

2·(a²+b²+c²+d²)−(a+b+c+d)²=0 mit a+b+c+d>0^{[6]:S. 2}

ist. Ein solches ganzzahliges Quadrupel besteht aus vier ganzen Zahlen.^[5]

• Das Stamm-Quadrupel (englisch root quadruple oder root packing) ist das Quadrupel mit den Krümmungen der vier größten Kreise in einer Füllung.^{[5]:S. 16}
• In einem primitiven ganzzahligen Descartes-Quadrupel sind die vier Zahlen teilerfremd.^{[5]:S. 3}

Die Ganzzahligkeit und Primitivität eines Stamm-Quadrupels überträgt sich auf die ihm entsprechende Apollonios-Kreisfüllung, die dann ebenso primitiv und ganzzahlig genannt wird.

Eigenschaften

Satz von Descartes

Der Satz von Descartes besagt, dass wenn {a,b,c,d} die Krümmungen von vier sich paarweise berührenden Kreisen sind, diese Krümmungen die descartsche Gleichung

2·(a²+b²+c²+d²)−(a+b+c+d)²=0

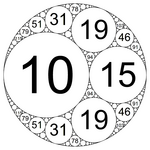
erfüllen. Die Krümmung eines umschreibenden Kreises geht hier mit negativem Vorzeichen ein. Wenn die Krümmungen der größten vier Kreise in der Füllung ganzzahlig sind, dann sind es deshalb auch die Krümmungen aller anderen Kreise in der Füllung.^[7] Im dritten Bild (C) oben hat der Umkreis die Krümmung 10 und die eingeschriebenen größten Kreise die Krümmungen 18, 23 und 27, womit auch alle anderen Kreise in der Füllung ganzzahlige Krümmungen aufweisen.

Wenn {a,b,c,d} ein Descartes-Quadrupel ist, dann ist es auch {a,b,c,d'} mit d'=2·(a+b+c)−d. Diese Krümmung hat derjenige Kreis, der durch Kreisspiegelung des Kreises mit Krümmung d an dem Kreis entsteht, der durch die drei Berührpunkte der Kreise mit Krümmungen a, b und c führt.^{[4]:S. 15}

Wenn {a,b,c,d} ein ganzzahliges Descartes-Quadrupel ist, dann folgt aus der descartschen Gleichung, dass (a+b+c+d)² eine gerade Zahl ist und somit auch die Summen a+b+c+d und −a+b+c+d gerade sind.

Stamm-Quadrupel

Betrachtet wird ein primitives ganzzahliges Descartes-Quadrupel ⅅ=(a,b,c,d) mit a+b+c+d > 0.

ⅅ ist ein Stamm-Quadrupel, wenn^{[5]:S. 15}

a ≤ 0 ≤ b ≤ c ≤ d und a+b+c ≥ d oder

a ≤ 0 ≤ b ≤ c ≤ d und 0 < d ≤ 2(a+b+c)−d

Für jedes nicht negative ganzzahlige n ist (−n, n+1, n(n+1), n(n+1)+1) ein Stamm-Quadrupel.^{[5]:S. 21} Hier kann der Kreis mit Krümmung n+1 wieder als Umkreis für eine Kreisfüllung (−n−1, n+2, (n+1)(n+2), (n+1)(n+2)+1) dienen und so weiter mit einem Ergebnis wie im Bild (B) oben. Diese Stamm-Quadrupel führen sämtlich auf #Symmetrische ganzzahlige Apollonios-Kreisfüllungen.

Alle Stamm-Quadrupel können mit der folgenden Methode gefunden werden.^{[5]:S. 19} Dazu werden neue Variablen x, d₁, d₂ und m gemäß

x = a, d₁ = a+b, d₂ = a+c, m = (a+b+c−d)/2

bzw.

a = x, b = d₁−x, c = d₂−x und d = d₁+d₂−x−2m

eingeführt. Dann gilt:

• x²+m² = d₁d₂
• ⅅ ist genau dann primitiv, wenn x, d₁ und d₂ teilerfremd sind.
• ⅅ ist genau dann ein Stamm-Quadrupel, wenn

x < 0 ≤ 2m ≤ d₁ ≤ d₂

Wegen 2m ≤ d₁ und 2m ≤ d₂ ist 4m² ≤ d₁d₂ und daher 3m² ≤ d₁d₂−m² = x². Die unten stehende, in der Programmiersprache Python geschriebene Funktion stammquadrupel gibt für eine ganze Zahl a die zu −|a| passenden Stamm-Quadrupel.

def stammquadrupel( a ):
    'gibt alle Stamm-Quadrupel ( −|a|, b, c, d )'
    import math
    assert a == int( a ), 'Aufruf: stammquadrupel( a ), a ganz'
    n   = abs( int( a ) )  # Ganzzahlarithmetik
    ans = []
    if n == 0:
        ans.append( ( 0, 0, 1, 1 ) )
    else: # n > 0
        for m in range( math.ceil( n/3**0.5 ) ):
            d1d2 = n**2 + m**2
            for d1 in range( max( 2*m, 1),
                             math.floor( d1d2**0.5 ) + 1 ):
                if d1d2%d1 == 0:
                    d2 = d1d2//d1
                    if math.gcd( n, math.gcd( d1, d2 ) ) == 1:
                        a = -n
                        b = d1 + n
                        c = d2 + n
                        d = d1 + d2 + n - 2*m
                        ans.append( ( a, b, c, d ) )
    return ans

Restklassen und die Lokal-Global-Vermutung

In einer spezifischen primitiven ganzzahligen Apollonios-Füllung zeigt sich immer, dass die Krümmungen bei Division durch 24 mit Rest nicht alle möglichen Reste 0 bis 23 lassen, sondern nur sechs bis acht von diesen. Beispielsweise sind die Krümmungen der 15 größten Kreise in der Füllung 10–18–23–27 im Bild (C) oben

−10, 18, 23, 27, 35, 47, 62, 63, 78, 83, 107, 110, 123, 135, 146.

Die Krümmung 10 des umschreibenden Kreises ist im Bild nicht angegeben und muss immer negativ genommen werden. Die Reste der Krümmungen bei Division durch 24 lauten

14, 18, 23, 3, 11, 23, 14, 15, 6, 11, 11, 14, 3, 15, 2

was ohne Doppeltnennungen

2, 3, 6, 11, 14, 15, 18, 23

entspricht. Die anderen 16 möglichen Reste, wie 1, 4 oder 5, können in der Füllung nicht vorkommen.

Denn in einer spezifischen primitiven ganzzahligen Apollonios-Füllung fallen die Krümmungen in sechs mögliche Restklassen­mengen modulo 24:^{[6]:S. 6}

{(0, 1, 4, 9, 12, 16), (0, 5, 8, 12, 20, 21), (0, 4, 12, 13, 16, 21), (0, 8, 9, 12, 17, 20)

(3, 6, 7, 10, 15, 18, 19, 22), (2, 3, 6, 11, 14, 15, 18, 23)}

Die Lokal-Global-Vermutung lautete, dass in einer Kreisfüllung (lokal) nur endlich viele Zahlen aus der jeweiligen Restklasse (global) nicht auftreten,^{[5]:S. 41} was 2023 zwei Studenten widerlegen konnten.^{[6]:S. 6[3]} Ein Gegenbeispiel ist im Bild (D) oben gezeigt. Die Krümmungen der größten zehn Kreise sind dort

−23, 48, 49, 52, 96, 105, 108, 193, 196, 208

und deren Reste modulo 24

1, 0, 1, 4, 0, 9, 12, 1, 4, 16

womit alle Elemente der ersten oben genannten Restklassenmenge 𝕄=(0, 1, 4, 9, 12, 16) modulo 24 vertreten sind. Allerdings kommen unendlich viele Elemente aus jeder der Restklassen in 𝕄 nicht als Krümmung in der Füllung vor.^{[6]:S. 4} Das ist nicht widersprüchlich, denn wenn man beispielsweise von allen positiven Ganzzahlen, die bei Division durch 24 den Rest eins lassen (das ist die Restklasse 1 modulo 24), die unendlich vielen Zahlen streicht, die den Rest 1 bei Division durch 48=2·24 lassen, bleiben immer noch unendlich viele Zahlen übrig.

Asymptotisches Verhalten

Zu jeder Füllung F gibt es Konstanten c_0,1,2>0, die nur von F abhängen, sodass^[8]

• die Anzahl N(T) der Kreise mit einer Krümmung kleiner als T für T→∞ asymptotisch gleich c₀·T^α ist,
• die Anzahl π(T) der Kreise mit einer primen Krümmung kleiner als T für T→∞ asymptotisch gleich c₁·T^α/log(T) ist,
• die Anzahl π₂(T) der Kreispaare mit Krümmungen, die kleiner als T sind und die einen Primzahlzwilling bilden, für T→∞ asymptotisch gleich c₂·T^α/log(T)² ist.

Darin ist α die Hausdorff-Dimension der Füllung.

Hausdorff-Dimension

Die Hausdorff-Dimension der Füllung ist ungefähr^[9]

α ≈ 1,3056867280498771846459862068510

Spezialfälle

Symmetrische ganzzahlige Apollonios-Kreisfüllungen

• Beispiele symmetrischer ganzzahliger Apollonios-Kreisfüllungen
• 
  Kreisfüllung (−1, 2, 2, 3)
• 
  Kreisfüllung (−3, 5, 8, 8)
• 
  Kreisfüllung (−12, 25, 25,28)
• 
  Kreisfüllung (−6, 10, 15, 19)

Die Tabelle enthält die Ausgaben von stammquadrupel(a) für a=0 bis a=14:

(0, 0, 1, 1)	(−1, 2, 2, 3)	(−2, 3, 6, 7)	(−3, 4, 12, 13)
(−3, 5, 8, 8)	(−4, 5, 20, 21)	(−4, 8, 9, 9)	(−5, 6, 30, 31)
(−5, 7, 18, 18)	(−6, 7, 42, 43)	(−6, 10, 15, 19)	(−6, 11, 14, 15)
(−7, 8, 56, 57)	(−7, 9, 32, 32)	(−7, 12, 17, 20)	(−8, 9, 72, 73)
(−8, 13, 21, 24)	(−8, 12, 25, 25)	(−9, 10, 90, 91)	(−9, 11, 50, 50)
(−9, 14, 26, 27)	(−9, 18, 19, 22)	(−10, 11, 110, 111)	(−10, 14, 35, 39)
(−10, 18, 23, 27)	(−11, 12, 132, 133)	(−11, 13, 72, 72)	(−11, 16, 36, 37)
(−11, 21, 24, 28)	(−12, 13, 156, 157)	(−12, 21, 28, 37)	(−12, 17, 41, 44)
(−12, 16, 49, 49)	(−12, 21, 29, 32)	(−12, 25, 25, 28)	(−13, 14, 182, 183)
(−13, 15, 98, 98)	(−13, 18, 47, 50)	(−13, 23, 30, 38)	(−14, 15, 210, 211)
(−14, 18, 63, 67)	(−14, 19, 54, 55)	(−14, 22, 39, 43)	(−14, 27, 31, 34)

Die rot markierten Quadrupel entsprechen Kreisfüllungen, die zu einem Durchmesser des Umkreises symmetrisch sind, auf dem der zweit- und drittgrößte Kreis der Füllungen liegen. Hier sind die viert- und fünftgrößten Kreise der Packung gleichgroß. Bei den grün markierten sind zwei der ersten vier größten Kreise in der Füllung gleich und die Symmetrieachse senkrecht zu ihrer Verbindungsachse. Bei den blau markierten Quadrupeln sind die Kreisfüllungen symmetrisch zu zwei zueinander senkrechten Symmetrieachsen.

Apollonios-Kreisfüllung 0–0–1–1

Die Apollonios-Kreisfüllung mit Stamm-Quadrupel 0–0–1–1

Die über Apollonios-Kreisfüllungen geltenden Aussagen erlauben auch die Krümmung null der Kreise, die dann zu Geraden entarten. Die Packung 0–0–1–1 besitzt zwei „Kreise“ mit unendlich fernen Mittelpunkten; diese Kreise degenerieren zu zwei parallelen Geraden im Abstand zwei. Zwischen diesen liegen unendlich viele Kopien der Packung mit dem Stamm-Quadrupel. Sie ist die einzige unbeschränkte Apollonios-Kreisfüllung.^{[5]:S. 3}

Indem nur ein Stück zwischen den Berührpunkten von zwei benachbarten Kreisen mit Krümmung eins und den Geraden herausgetrennt wird, ihre Größe halbiert wird und nur die Kreise betrachtet werden, die eine der beiden Geraden berühren, bleiben Ford-Kreise zurück, die in der Zahlentheorie eine Rolle spielen.

Apollonios-Gruppe

Die Apollonios-Gruppe A ist eine Gruppe, die von den vier selbstinversen Matrizen^{[4]:S. 21}

${\displaystyle {\mathsf {S}}_{1}={\scriptstyle {\begin{pmatrix}-1&2&2&2\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}},\,{\mathsf {S}}_{2}={\scriptstyle {\begin{pmatrix}1&0&0&0\\2&-1&2&2\\0&0&1&0\\0&0&0&1\end{pmatrix}}},\,{\mathsf {S}}_{3}={\scriptstyle {\begin{pmatrix}1&0&0&0\\0&1&0&0\\2&2&-1&2\\0&0&0&1\end{pmatrix}}},\,{\mathsf {S}}_{4}={\scriptstyle {\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\2&2&2&-1\end{pmatrix}}}}$

erzeugt wird, mit denen sich sämtliche Elemente der Gruppe durch Matrizenmultiplikation berechnen. Wenn die Koeffizienten des Spaltenvektors q=(w,x,y,z)^⊤ ein Descartes-Quadrupel sind, dann ist es Mq mit M∈A ebenfalls.

Verallgemeinerungen

Apollonische Kugelpackung

Im n-dimensionalen Raum besteht eine Füllung aus n+2 paarweise berührenden n−1-Sphären, die sich in verschiedenen Punkten berühren.^{[10]:S. 2} In der euklidischen Geometrie existieren ganzzahlige Packungen aus sich berührenden Sphären, die die verallgemeinerte Descartes-Gleichung^{[11]:S. 512}

${\displaystyle \left(\sum _{i=1}^{n+2}r_{i}^{-1}\right)^{2}-n\sum _{i=1}^{n+2}r_{i}^{-2}=0}$

befolgen, nur in zwei und drei Dimensionen; in höheren Dimensionen überlappen sich die Sphären.^{[10]:S. 22[4]:S. 3}

Die Packung wurde auch in der höherdimensionalen sphärischen^{[11]:S. 511} und hyperbolischen Geometrie untersucht.^{[11]:S. 515} Es gibt auch dort ganzzahlige Packungen.^{[5]:S. 7} Auf der rechten Seite obiger Gleichung ersetzt in sphärischer Geometrie ein negativer Wert^{[10]:S. 11} die Null und in der hyperbolischen ein positiver.^{[10]:S. 17[12]:S. 3}

Geschichte

1643 entdeckte René Descartes den nach ihm benannten Satz, aber erst 1936 fiel es Frederick Soddy auf, dass es ganzzahlige Kreispackungen gibt, was er in Form des Gedichts „The Kiss Precise“ veröffentlichte;^[7] weitere Details dazu wurden 1937 bekannt.^[13] Der Name „apollonian packing“ geht auf Kasner und Supnick^[14] aus dem Jahr 1943 zurück und wurde 1982 von B. Mandelbrot^[15] populär gemacht, der einen Zusammenhang mit dem Werk von Apollonios von Perge um 200 v. Chr. feststellte.^{[5]:S. 6}

Weblinks

Literatur

1. Dietmar Herrmann: Die antike Mathematik. Eine Geschichte der griechischen Mathematik, ihrer Probleme und Lösungen. Springer Spektrum, Berlin, Heidelberg 2014, ISBN 978-3-642-37611-5, S. 374, doi:10.1007/978-3-642-37612-2. 
2. C. Pöppe: Kreispackungen. Spektrum.de, 1. November 2002, abgerufen am 7. November 2023. 
3. M. G. Levy: Zwei Studierende widerlegen eine anerkannte Vermutung über Fraktale. Spektrum.de, 30. August 2023, abgerufen am 7. November 2023. 
4. R. L. Graham, J. C. Lagarias, C. L. Mallows, A. R. Wilks: Apollonian Circle Packings: Geometry and Group Theory I. The Apollonian Group. In: Discrete and Computational Geometry. Band 34, 11. März 2005, S. 547–585, doi:10.48550/arXiv.math/0010298, arxiv:math/0010298v5 (englisch). 
5. R. L. Graham, J. C. Lagarias, C. L. Mallows, A. R. Wilks, C.H. Chan: Apollonian Circle Packings: Number Theory. In: J. Number Theory. Band 100, 17. Oktober 2003, S. 1–45, doi:10.48550/arXiv.math/0009113, arxiv:math/0009113v2 (englisch). 
6. S. Haag, C. Kertzer, J. Rickards, K. E. Stange: The Local-Global Conjecture for Apollonian circle packings is false. In: Number Theory (math.NT). 21. Juli 2023, S. 1–28, doi:10.48550/arXiv.2307.02749, arxiv:2307.02749v2 [abs] (englisch). 
7. Frederick Soddy: The Kiss Precise. In: Nature. Band 137, Nr. 1021, 20. Juni 1936, doi:10.1038/1371021a0. 
8. A. Kontorovich, H. Oh: Apollonian circle packings and closed horospheres on hyperbolic 3-manifolds. 2010, arxiv:0811.2236v5. 
9. Zai-Qiao Bai, S. R. Finch: Precise Calculation of Hausdorff Dimension of Apollonian Gasket. In: Fractals. Band 26, Nr. 4, 2018, doi:10.1142/S0218348X18500500 (englisch, researchgate.net [abgerufen am 26. Oktober 2023]). 
10. J. C. Lagarias, C. L. Mallows, A. R. Wilks: Beyond the Descartes circle theorem. In: Amer. Math. Monthly. Band 109, 9. Januar 2001, S. 338–361, doi:10.48550/arXiv.math/0101066, arxiv:math/0101066 (englisch). 
11. J. G. Mauldon: Sets of equally inclined spheres. In: Canadian J. Math. Band 14, 1962, S. 509–516, doi:10.4153/CJM-1962-042-6. 
12. N. Eriksson, J.C. Lagarias: Apollonian circle packings: Number theory II. Spherical and hyperbolic packings. In: The Ramanujan Journal. Band 14, Nr. 3, 9. Oktober 2007, S. 437–469, doi:10.1007/s11139-007-9052-6, arxiv:math/0403296 (englisch). 
13. The Kiss Precise. In: Nature. Band 139, Nr. 62, 9. Januar 1937, doi:10.1038/139062a0. 
14. E. Kasner, F. Supnick: The Apollonian packing of circles. In: Proceedings of the National Academy of Sciences USA. Band 29, Nr. 11, 1943, S. 378–384, doi:10.1073/pnas.29.11.378, PMID 16588629, PMC 1078636 (freier Volltext). 
15. B. Mandelbrot: The Fractal Geometry of Nature. W. H. Freeman, New York 1983, ISBN 0-7167-1186-9, S. 170 (archive.org).