Dreißigeck

Regelmäßiges Dreißigeck

Das Dreißigeck oder Triakontagon (von altgriechisch τριάκοντα triákonta, deutsch ‚dreißig‘ und γωνία gōnía, deutsch ‚Winkel, Ecke‘)^[1] ist eine geometrische Figur und ein Vieleck (Polygon). Es ist bestimmt durch dreißig Eckpunkte und deren dreißig Verbindungen namens Strecken, Seiten oder Kanten.

Variationen

Das Dreißigeck ist darstellbar als:

• konkaves Dreißigeck, in dem mindestens ein Innenwinkel größer als 180° ist.
• konvexes Dreißigeck, in dem alle Innenwinkel kleiner als 180° sind. Ein konvexes Dreißigeck kann regelmäßig oder unregelmäßig sein.
• Sehnendreißigeck, in dem alle Ecken auf einem gemeinsamen Umkreis liegen, aber die Seitenlängen möglicherweise ungleich sind.
• regelmäßiges Dreißigeck: Es ist bestimmt durch dreißig Punkte, die auf einem virtuellen oder realen Kreis liegen. Die benachbarten Punkte haben zueinander stets den gleichen Abstand und sind mittels aneinandergereihten Strecken, auch Seiten oder Kanten genannt, verbunden.
• regelmäßiges überschlagenes Dreißigeck: Es ergibt sich, wenn beim Verbinden der dreißig Eckpunkte jedes Mal mindestens einer übersprungen wird und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen ${\displaystyle \left\{n/k\right\}}$, wobei ${\displaystyle n}$ die Anzahl der Eckpunkte angibt und jeder ${\displaystyle k}$-te Punkt verbunden wird.

Es gibt nur drei regelmäßige Dreißigstrahlsterne.

Die „Sterne“ mit den Symbolen {30/2} und {30/28} sind regelmäßige Fünfzehnecke, {30/3} und {30/27} regelmäßige Zehnecke, {30/5} und {30/25} regelmäßige Sechsecke, {30/6} und {30/24} regelmäßige Fünfecke, {30/10} und {30/20} gleichseitige Dreiecke. Die Sterne mit den Symbolen {30/4} und {30/26}, {30/8} und {30/22} sowie {30/14} und {30/16} sind regelmäßige Fünfzehnstrahlsterne, {30/9} und {30/21} regelmäßige Zehnstrahlsterne und schließlich {30/12} und {30/18} regelmäßige Pentagramme.

• Regelmäßige überschlagene Dreißigecke
• 
  ${\displaystyle \left\{30/7\right\}{,}\ \left\{30/23\right\}}$
• 
  ${\displaystyle \left\{30/11\right\}{,}\ \left\{30/19\right\}}$
• 
  ${\displaystyle \left\{30/13\right\}{,}\ \left\{30/17\right\}}$

Regelmäßiges Dreißigeck

Das regelmäßige Dreißigeck ist nach Carl Friedrich Gauß und Pierre-Laurent Wantzel ein konstruierbares Polygon, da die Anzahl seiner Seiten als Produkt einer Zweierpotenz mit paarweise voneinander verschiedenen Fermatschen Primzahlen (${\displaystyle 30=2^{1}\cdot 3\cdot 5}$) darstellbar ist.

Größen

Die Größen und deren allgemeine Formeln sind in Fünfzehneck, Mathematische Zusammenhänge ausführlich beschrieben.

Größen eines regelmäßigen Dreißigecks[2]
Innenwinkel	${\displaystyle {\begin{aligned}\alpha &={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {28}{30}}\cdot 180^{\circ }\\&=168^{\circ }\end{aligned}}}$
Zentriwinkel (Mittelpunktswinkel)	${\displaystyle {\begin{aligned}\mu &={\frac {360^{\circ }}{30}}\\\mu &=12^{\circ }\end{aligned}}}$
Seitenlänge	${\displaystyle {\begin{aligned}a&=R\cdot {\frac {1}{4}}\cdot \left({\sqrt {6\cdot \left(5-{\sqrt {5}}\right)}}-{\sqrt {5}}-1\right)\\&={\frac {\sin(12^{\circ })}{\sin(84^{\circ })}}\cdot R\\&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{30}}\right)\approx 0{,}2090569\cdot R\end{aligned}}}$
Umkreisradius	${\displaystyle {\begin{aligned}R&=a\cdot {\frac {1}{2}}\cdot \left(2+{\sqrt {5}}+{\sqrt {15+6\cdot {\sqrt {5}}}}\right)\\&={\frac {\sin(84^{\circ })}{\sin(12^{\circ })}}\cdot a\\&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{30}}\right)}}\approx 4{,}783386\cdot a\end{aligned}}}$
Inkreisradius	${\displaystyle {\begin{aligned}r&=a\cdot {\frac {1}{4}}\cdot \left({\sqrt {15}}+3\cdot {\sqrt {3}}+{\sqrt {2}}\cdot {\sqrt {25+11\cdot {\sqrt {5}}}}\right)\\&={\frac {\sin ^{2}(84^{\circ })}{\sin(12^{\circ })}}\cdot a\approx 4{,}757182\cdot a\end{aligned}}}$
Höhe	${\displaystyle {\begin{aligned}h&=2\cdot r\approx 9{,}514364\cdot a\end{aligned}}}$
Flächeninhalt	${\displaystyle {\begin{aligned}A&=a^{2}\cdot {\frac {15}{4}}\cdot \left({\sqrt {15}}+3\cdot {\sqrt {3}}+{\sqrt {2}}\cdot {\sqrt {25+11\cdot {\sqrt {5}}}}\right)\\&=15\cdot {\frac {\sin ^{2}(84^{\circ })}{\sin(12^{\circ })}}\cdot a^{2}\approx 71{,}357733\cdot a^{2}\end{aligned}}}$

Konstruktion mit Zirkel und Lineal bei gegebenem Umkreis

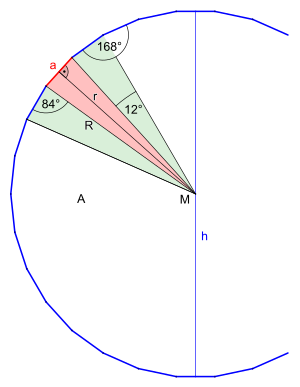
Bild 1b: Dreißigeck, ohne Konstruktion des Fünfzehnecks

Bild 1a: Fünfzehneck

Im ersten Moment scheint es naheliegend, zuerst eine Seitenlänge des Fünfzehnecks mit dessen Umkreis zu zeichnen und anschließend den Zentriwinkel ${\displaystyle \mu }$ zu halbieren, um die Seitenlänge des Dreißigecks zu erhalten. Sieht man jedoch auf die Zeichnung des Fünfzehnecks, ist gut erkennbar, die Mittelachse ${\displaystyle {\overline {AB}}}$ ist bereits eine Winkelhalbierende zwischen den Eckpunkten ${\displaystyle E_{3}}$ und ${\displaystyle E_{4}}$ (siehe Bild 1a). Folglich wären die Strecken ${\displaystyle {\overline {AE_{3}}}}$ sowie ${\displaystyle {\overline {AE_{4}}}}$ bereits Seitenlängen und der Winkel ${\displaystyle E_{3}MA}$ der Zentriwinkel eines Dreißigecks. Es bedarf also stattdessen nur der Seitenlänge des Fünfecks um den Zentriwinkel sowie die erste Seitenlänge des Dreißigecks zu finden. Die nun folgende Konstruktion (siehe Bild 1b) nutzt diese Möglichkeit.

Es beginnt mit dem Ziehen des Kreises ${\displaystyle k_{1}}$ um den Mittelpunkt ${\displaystyle M,}$ dem Einzeichnen der Mittelachse ${\displaystyle {\overline {AB}}}$ und der Orthogonalen ${\displaystyle {\overline {MC}}.}$ Es folgt die Halbierung der Strecke ${\displaystyle {\overline {AM}}}$ in ${\displaystyle D,}$ dabei ergeben sich die ersten Eckpunkte ${\displaystyle E_{5}}$ und ${\displaystyle E_{25}}$ des entstehenden Dreißigecks. Der Kreisbogen um den Punkt ${\displaystyle D}$ mit dem Radius ${\displaystyle {\overline {CD}}}$ schließt sich an; der Schnittpunkt auf ${\displaystyle {\overline {AB}}}$ ist ${\displaystyle F.}$ Nun schlägt man einen kurzen Kreisbogen um den Eckpunkt ${\displaystyle E_{25}}$ mit dem Radius ${\displaystyle {\overline {CF}}}$, bis er den Umkreis in ${\displaystyle E_{1}}$ schneidet. Die Strecke ${\displaystyle {\overline {AE_{1}}}}$ ist die gesuchte Seitenlänge ${\displaystyle a}$ des Dreißigecks mit dessen Zentriwinkel ${\displaystyle \mu =12^{\circ }.}$ Nun die Seitenlänge ${\displaystyle a}$ in den Zirkel nehmen, die restlichen Eckpunkte gegen den Uhrzeigersinn auf den Umkreis abtragen und abschließend die benachbarten Eckpunkte miteinander verbinden. Das regelmäßige Dreißigeck ist somit fertiggestellt.

Konstruktion mit Zirkel und Lineal bei gegebener Seitenlänge

Bild 2: Regelmäßiges Dreißigeck bei gegebener Seitenlänge

Die Konstruktion im Bild 2 ist nahezu gleich der des Fünfzehnecks bei gegebener Seitenlänge.

Zuerst werden die Enden der Seitenlänge ${\displaystyle a}$ mit den ersten Eckpunkten ${\displaystyle E_{1}}$ (links) bzw. ${\displaystyle E_{2}}$ bezeichnet, anschließend verlängert man die Strecke ${\displaystyle {\overline {E_{1}E_{2}}}}$ über ${\displaystyle E_{1}}$ hinaus um ca. den gleichen Längenbetrag. Es folgt ein Kreisbogen mit dem Radius ${\displaystyle {\overline {E_{1}E_{2}}}}$ um den Punkt ${\displaystyle E_{1},}$ die Orthogonale ${\displaystyle {\overline {E_{1}A}}}$ und der Kreisbogen um ${\displaystyle E_{2},}$ ebenfalls mit dem Radius ${\displaystyle {\overline {E_{1}E_{2}}};}$ dabei entstehen die Schnittpunkte ${\displaystyle B}$ und ${\displaystyle C.}$ Nun wird eine Halbgerade ab ${\displaystyle C}$ durch ${\displaystyle B}$ gezeichnet; sie halbiert die Seitenlänge ${\displaystyle a}$ in ${\displaystyle D.}$ Der nächste Kreisbogen mit dem Radius ${\displaystyle |AD|}$ wird um ${\displaystyle D}$ gezogen, dabei ergibt sich der Schnittpunkt ${\displaystyle F}$ auf der Verlängerung. Die Strecke ${\displaystyle {\overline {E_{2}F}}}$ ist somit nach dem goldenen Schnitt mit äußerer Teilung geteilt.

Jetzt wird um ${\displaystyle E_{2}}$ ein Kreisbogen mit dem Radius ${\displaystyle {\overline {E_{2}F}}}$ geschlagen, der die Halbgerade in ${\displaystyle G}$ schneidet. Die damit erzeugte Strecke ${\displaystyle {\overline {CG}}}$ entspricht dem Umkreisradius eines Fünfzehnecks. Die Berechnung des Umkreisradius ${\displaystyle {\overline {CG}}}$ ist im Artikel Fünfzehneck ausführlich beschrieben. Die Strecke ${\displaystyle {\overline {CG}}}$ in den Zirkel genommen und um ${\displaystyle E_{2}}$ einen kurzen Kreisbogen durch die Halbgerade gezogen, ergibt den Mittelpunkt ${\displaystyle H}$ des Umkreises eines nicht eingezeichneten Fünfzehnecks mit dessen Zentriwinkel ${\displaystyle \mu _{1}=24^{\circ }.}$

Es geht weiter mit dem Kreisbogen um den Punkt ${\displaystyle H}$ mit dem Radius ${\displaystyle {\overline {E_{1}H}},}$ der die Halbgerade in ${\displaystyle M}$ schneidet. Wegen ${\displaystyle {\overline {E_{1}H}}={\overline {HM}}}$ ist nach dem Zentriwinkelsatz der Winkel ${\displaystyle \mu }$ am Winkelscheitel ${\displaystyle M}$ halb so groß, als der Zentriwinkel ${\displaystyle \mu _{1}}$ eines Fünfzehnecks. Aufgrund dessen ist ${\displaystyle M}$ der Mittelpunkt des gesuchten Dreißigecks mit dessen Zentriwinkel ${\displaystyle \mu =12^{\circ }.}$ Jetzt nur noch den Umkreis um den Mittelpunkt ${\displaystyle M}$ ziehen, die Seitenlänge ${\displaystyle a}$ 29-mal gegen den Uhrzeigersinn auf den Umkreis abtragen und die benachbarten Eckpunkte miteinander verbinden, danach ist das regelmäßige Dreißigeck konstruiert.

Diagonalen

Bild 3: Dreißigeck,
Diagonalen ${\displaystyle d_{2}}$ bis ${\displaystyle d_{15}}$ (Durchmesser)

Jedes Dreißigeck besitzt 405 Diagonalen. Für jede der 30 Ecken, an der eine Diagonale anfangen kann, gibt es 27 mögliche Endpunkte. Diese Anzahl muss aber noch durch 2 geteilt werden, damit keine Diagonale doppelt gezählt wird. So ergeben sich die genannten ${\displaystyle {\tfrac {30\cdot 27}{2}}=405}$ Diagonalen. Davon sind aber nur ${\displaystyle \left\lfloor {\tfrac {30-2}{2}}\right\rfloor =14}$ verschieden lang. Allgemein wird mit ${\displaystyle d_{n}}$ diejenige Diagonale bezeichnet, die über ${\displaystyle n}$ Seiten des Polygons verläuft, demzufolge verläuft z. B. die Diagonale ${\displaystyle d_{14}}$ über vierzehn Seiten.

Goldener Schnitt

Da 5 der Ecken des regelmäßigen Dreißigecks ein regelmäßiges Fünfeck bilden, stehen die Diagonale über 12 Seiten ${\displaystyle d_{12}}$ und die Diagonale ${\displaystyle d_{6}}$ im Verhältnis des Goldenen Schnittes zueinander.

Außerdem findet sich dieses Verhältnis bei ${\displaystyle d_{5}}$ mit ${\displaystyle d_{3}}$, diese Diagonalen sind Teil eines regelmäßigen Zehnecks, und bei ${\displaystyle d_{9}}$ mit ${\displaystyle d_{5}}$. ${\displaystyle d_{5}}$ ist eine Seitenlänge des regelmäßigen Sechsecks und hat somit die gleiche Länge wie der Umkreisradius ${\displaystyle R}$ des Dreißigecks. Also bildet ${\displaystyle R}$ auch mit ${\displaystyle d_{9}}$ den Goldenen Schnitt als Verhältnis.

Andere Verhältnisse

Die Diagonale ${\displaystyle d_{10}}$ steht zu ${\displaystyle d_{5}}$ im Verhältnis ${\displaystyle {\sqrt {3}}}$.

Vorkommen

Wiener Riesenrad im Minimundus
mit 30 Ecken und 15 Waggons

• Das Wiener Riesenrad besitzt die Form eines regelmäßigen Dreißigecks. Obwohl seit 1945 nur 15 Waggons eingehängt sind, wurde es ursprünglich für 30 Waggons gebaut.
• Der Grundriss des Zirkus Sarrasani ist ein regelmäßiges Dreißigeck.^[3]

Siehe auch

• Sehnenvieleck
• Regelmäßiges Polygon

Literatur

• H. Maser: Die Teilung des Kreises ..., Artikel 365., in Carl Friedrich Gauss' Untersuchungen über höhere Arithmetik, Verlag von Julius Springer, Berlin 1889; Göttinger Digitalisierungszentrum, Universität Göttingen; abgerufen am 15. März 2018.

Weblinks

• Regelmäßiges Dreißigeck, Mathematik alpha

Einzelnachweise

1. Wilhelm Pape, Max Sengebusch (Bearb.): Handwörterbuch der griechischen Sprache. 3. Auflage, 6. Abdruck. Vieweg & Sohn, Braunschweig 1914 (zeno.org [abgerufen am 2. Juli 2024]).  (S. 1139, Spalte 2, 3. Eintrag; Wort von OCR nicht erfasst)
2. Eric W. Weisstein: Triacontagon. In: WolframMathWorld. Abgerufen am 13. März 2018. 
3. Ing. Ludw. Fischer: Moderner Zirkus. Mitteilungen aus verschiedenen Fachgebieten. In: kobv.de – Kooperativer Bibliotheksverbund Berlin-Brandenburg. Zeitschrift des österreichischen Ingenieur- und Architekten-Vereins Nr. 23, 1913, S. 410–411, PDF-Datei: Seite 58–59, abgerufen am 11. März 2018.